
How Does a Bicycle Work? A New Instrument to Assess Mechanical Reasoning in School Aged Children
[¿Cómo funciona una bicicleta? Un nuevo instrumento para evaluar el razonamiento mecánico en alumnos de primaria ]
Elenora Cannoni, Anna Silvia Bombi, Gemma Marano and Anna Di Norcia
Sapienza University of Rome, Italy
https://doi.org/10.5093/psed2018a10
Received 21 June 2017, Accepted 16 March 2018
Abstract
This study demonstrated that a brief interview can reveal the mechanical reasoning that could not be assessed via the Bicycle Drawing Test. This study, conducted on 190 children (6 to 11 years old), shows that mechanical reasoning improves with age. It shows correlations with spatial reasoning and motor control, and with visual reasoning.
Resumen
El estudio demostró que una breve entrevista puede revelar el razonamiento mecánico que no se pudo evaluar a través de la prueba de dibujo de bicicletas. Un estudio realizado en 190 niños (de 6 a 11 años) muestra que el razonamiento mecánico mejora con la edad. Este studio muestra correlaciones con razonamiento espacial y control motor y también con razonamiento visual.
Palabras clave
Razonamiento mecánico, Prueba de dibujo de bicicletas, Infancia, Entrevista.
Keywords
Mechanical reasoning, Bicycle Drawing Test, Childhood, Interview.
Cite this article as: Cannoni, E., Bombi, A. S., Marano, G., & Di Norcia, A. (2018). How does a bicycle work? A new instrument to assess mechanical reasoning in school aged children. Psicología Educativa, 24, 59-62. https://doi.org/10.5093/psed2018a10
Funding: This study was partially supported by Grant Ateneo 2016 from Sapienza, Rome University.
Correspondence: anna.dinorcia@uniroma1.it (A. Di Norcia).
Introduction When a person is required to explain how a bicycle works, he/she must apply mechanical inferences. According to Hegarty (2004), a mechanical inference is the mental process that allows us to derive information about how things move: an inference is a cognitive process in which new information is derived from given information, and mechanics is the branch of physics that studies motion. Empirical works with adults were aimed at illustrating what kind of mechanical reasoning characterizes the so called “naïve physics” (diSessa, 1993). Participants in these studies were tipically asked to infer the functioning of a mechanical system from a visual spatial representation, such as a diagram (Hegarty, 2004). As regards children, research about mechanical reasoning dates back to the classical Piagetian study about physical causality (Piaget, 1927, reprint of the English translation 2013). According to Piaget, mechanical reasoning is only one of the 17 types of causal explanations that are possible to conceive. As he summarizes in the final chapter of his book, nine of these kinds of explanations can be defined “pre-causal”, since they imply “a confusion of relations of a psychological or biological type in general with relations of a mechanical type” (Piaget, 1927, p. 267 of the English translation, 2103). Mechanical causality, i.e., an explanation based on the contact of material entities and transfer of movement, is one of the eight “rational forms” of causality. It is one of the earlier to appear around 7-8 years of age. It is preceded by circular explanations, according to which an object (e.g., a cloud) once set in motion pushes the surrounding medium (the air), which in turn maintains the movement of the object (the wind pushes the cloud). In the mechanical explanation this circularity disappears: the wind pushes the cloud, but is not created by the cloud itself. Complementing his usual verbal technique with the request of drawing a bicycle, Piaget found a strict relationship between the drawing of the bicycle and the explanation of its mechanism: when school-age children (around 8 years of age) succeeded in drawing a complete bicycle, they were also able to say how it works. Based on this Piagetian work, some authors (Lebrun and Hoops, 1974; Lezak, 1976, now available in Lezak, Howieson, Bigler, & Tranel, 2012; Taylor, 1959) have proposed to use the bicycle drawing as a measure of mechanical reasoning, as well as of visual and graphic skills. The Bicycle Drawing Test (BDT) developed by these scholars is often used with children because it is an attractive task, easy and quick to administer. The BDT differentiates between typical and clinical subjects with various kinds of mental problems, such as autism (Levi, Penge, & Iacovelli, 1990) or cerebral damages (Sandyk, 1998). For these reasons it has been recommended as a useful tool in neuropsychological screening (Lezak et al., 2012) and developmental assessment (Tavano et al., 2007). About two decades ago, to make the test more sensitive to clinical cases, Greenberg, Rodriguez, and Sesta (1994) proposed a scoring based on 26 items, grouped into four categories: general knowledge of the bicycle parts, motor control, spatial reasoning, and mechanical reasoning. This coding system was used by Cannoni, Di Norcia, Bombi, and Di Giunta (2015) in a validation study with typically developing children. With a series of explorative and confirmative factor analyses, these authors came to a much shorter coding system (9 items), pertaining to only two dimensions: spatial reasoning and visual-motor control. According to Cannoni et al. (2015), the items originally included by Greenberg et al. (1994) to test mechanical reasoning failed to aggregate in a separate factor, and did not fulfill the measurement invariance requirement. As a consequence, this recent study seems to demonstrate that drawing a bicycle, even if useful for other aims, is not a valid measure of mechanical reasoning. The results obtained by Cannoni et al. (2015) also seem to disconfirm the original claim of Piaget (1927) that it would be possible to use drawings to detect children’s understanding of mechanical causality. Piaget, however, suggested complementing the drawing of the bicycle with verbal questions about its functioning, as it was typical of his “clinical” approach. Based on the classic Piagetian procedure, the aim of the present study is to investigate whether a brief interview can reveal reasoning skills that do not emerge from the drawing. We expect that mechanical reasoning skills as measured by the interview would improve with age. We will also explore gender differences, because boys performed better than girls in the BDT component linked to mechanical reasoning (Greenberg et al., 1994). As in the classical Piagetian study, we expect a relationship between the accuracy of drawing and verbal explanations, because of the demonstrated correlation between mechanical reasoning and spatial visual information (Hegarty, 2004). But this relation could be modest, because our previous work showed that BDT is not a valid measure of mechanical reasoning (Cannoni et al. 2015), while the interview would provide additional information that the drawing does not show. We finally expect a relationship between mechanical reasoning and visual-spatial reasoning as measured by the Coloured Matrices (Raven, 1994), because both these forms of reasoning require the skill of finding logical associations on a visual perceptive foundation. At the same time, the relation between these two constructs could be modest, because they also require specific skills: in fact knowledge about bicycle functioning is required for drawing, but it is not necessary for completing the Coloured Matrices Test. In conclusion, the skills measured by these tests are only in part similar. MethodParticipants A total of 190 primary school children from 6 to 11 years old participated in the current study (mean age = 8.7 years, SD = 1.4). Participants were distributed by age and gender as follows: 6 years, 15 boys and 17 girls; 7 years, 19 boys and 13 girls; 8 years, 13 boys and 30 girls; 9 years, 26 boys and 19 girls; 10 years 18 boys and 20 girls; in total 91 boys and 99 girls. Children participated in the research with the consent of their parents that were informed about the general research aims and about the privacy rules followed by researchers. Children were free to refuse to participate or to interrupt their participations at any moment. Measures Drawings. Each child was asked to draw a bicycle “as best as you can” on a A4 sheet (21.0 x 29.7 cm) with the long side horizontal, using only a pencil; following Lezak et al. (2012), erasing was not permitted. Drawings were scored using the system proposed by Cannoni et al. (2015), which includes two scales, spatial reasoning and visual-motor control, composed respectively of 5 and 4 items, each scored 0 or 1; the first scale takes into account the child’s ability to give depth and proportion to the parts, to connect them correctly to each other and to include elements that, in a canonical side-view of the bike, “pierce the page” (handlebars, pedals); the second scale is based on the quality of execution of wheels, which must be of the same size, not too elliptical, without angles and provided with spokes correctly distributed within the wheel frame. Mechanical reasoning interview. After finishing the drawing, children were asked to explain “how the bicycle works” (if necessary, specifying: “how does it move?”) and to indicate the function of the drawn parts. Finally, if the child had not made any reference to the mechanisms of transmission of the movement, he/she was asked: “How does it happen that when you push on the pedals the wheels spin?” Interviews were coded for the quality of reference to 3 items: “pedals”, “wheels”, “chain”. The scores were as follows: 0 = part named but with a wrong function, 1 = part named without reference to its function, 2 = part and general function named without further explanations, 3 = part named and function explained in terms of indirect connections, and 4 = part named and function explained by a series of mechanical links. The total mechanical reasoning score was then computed summing the scores of three items only: “pedals”, “wheels”, and “chain” (theoretical range 0-12). Two independent raters scored 30% of the interviews (n = 57). The interrater reliability for the total score was Pearson’s r = .96. Coloured Matrices. (CPM; Raven, 1954). It is a test requiring visual-spatial analysis and logical reasoning and it is used to assess the components of fluid intelligence. The CPM were scored according the original manual (Raven, 1954): 1 point was assigned to each correct item (range 0-36). The test was validated on the Italian population by Belacchi, Scalisi, Cannoni, and Cornoldi (2008). Procedure With the consent of families and schools, the Colored Progressive Matrices (CPM), the Bicycle Drawing Test (BDT), and the Mechanical reasoning interview were administered to children. Drawings and interviews were collected individually in the same session. Later, we collectively administered the Coloured Matrices. Data Analyses ANOVAs were conducted to verify age and gender differences in the mechanical reasoning score; post-hoc analysis was conducted using the Tukey-b test. To verify the relation between mechanical reasoning and visual-spatial reasoning (as measured by CPM), spatial reasoning and visual-motor control (as measured by drawing), Pearson’s r correlations were carried out, controlling for age. ResultsThe analysis of variance conducted on the mechanical reasoning score by gender and age showed main effects of age, F(4, 189) = 7.35, p < .001, pη2 = .14. No differences emerged between boys and girls, F(1, 189) = 1.63, p = .20, pη2 = .01. The interaction between the two factors was not significant, F(1, 189) = .773, p = .55, pη2 = .02. The Tukey test showed that 10 year old children’s scores in mechanical reasoning were significantly higher than 6 year old children, while other children obtained intermediate scores (see Table 1).
Table 1 Discussion and Conclusion Mechanical Reasoning Descriptive Statistics by Age 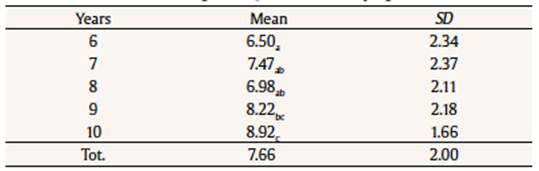 Note. Means followed by a different subscript differ at p < .05. Correlations between verbal mechanical reasoning and other measures were modest but statistically significant: visual-spatial reasoning, r = .33 (p < .001), spatial reasoning, r = .27 (p < .001), and motor control, r = .17 (p = .02). The aim of the present work was to verify if interviewing children about how a bicycle works would supply some information about mechanical reasoning that drawings do not offer, according to Cannoni et al. (2015). As expected, the mechanical reasoning skills derived by interview gradually improved with age during primary school’s years. Considering that the answers about pedals, chain, and wheels could provide a maximum of 12 points, we see that the explanations are not as comprehensive as they appeared from the Piagetian study (Piaget, 1927). The children of the lower age group, whose average score is around 7 points, noted the main pieces that form the vehicle and described accurately one or two of them. The older children (9 and 10 years of age) reached in general a score of 8-9 points, because they named the functions of the various parts, but without the completeness and accuracy that would allow them to achieve the maximum score. We noted that children’s drawings, as well as their verbal explanations, were much worse than those obtained by Piaget with children of the same age. Probably, the lesser presence of bicycles in the contemporary urban setting can explain this difference; studies on the visual representation and drawing of bicycles in adults (Hubley & Hamilton, 2002; Lawson, 2006) show that this task is hard for adults too, especially representing the transmission of motion. Differently from Greenberg et al. (1994), we did not find gender differences. Probably the boys’ superiority found by Greenberg et al. (1994) was specific of the graphic representation of the bicycle mechanism and it could not be extended to mechanical reasoning in general. As expected, we found modest but significant correlations between interview scores and BDT measures. This result confirms that some relationship between the accuracy of the bike drawing and the verbal explanation of its functioning does exist, but the drawing alone is not sufficient to access children’s mechanical competence. Drawing provides information about two abilities, spatial reasoning and motor control, that are relevant for, but not coincident with, mechanical reasoning. We can speculate that the drawing represent for children a sort of diagram that helps them in the explanation, as in the studies reviewed by Hegarty (2004). The modest but significant correlation between mechanical reasoning and visual spatial reasoning (as measured by CPM) probably means that mechanical reasoning is a specific component, not overlapping with fluid intelligence measured by this test. As we speculated in our hypothesis, both drawing and completing CPM require to find logical associations using a visual perceptive skills, but only drawing requires specific knowledge about bicycle functioning. In conclusion our study shows that a few direct questions can complement BDT with a measure of mechanical reasoning, clarifying the level of the child’s conceptions about how the bicycle works. This can be relevant for those who want to capitalize on the easy administering of the BDT and on the new, short coding system proposed by Cannoni et al. (2015): in fact, the length of the verbal interview required to verify if children do have some ideas about the bicycle mechanisms is very modest, and the coding almost immediate. For these reasons we would like to propose the combination of the pictorial test with the verbal inquiry, going back to the original Piagetian proposal. In this way, a more complete instrument would be available for screenings with large groups of children. This is only a small contribution to a large, and seldom explored field, but it offers some advantages in knowledge; in fact it demonstrate that interviewing children about their pictorial representation could improve information about their reasoning. Through drawing, the psychologist can obtain information about motor control and visual motor skills, but only through questions he/she can really investigate mechanical reasoning. The combination of drawing and verbal explanation can be also useful in educational contexts. As shown by Mason, Lowe, and Tornatora (2013), children asked to draw a mechanical device gathered a better understanding of its functioning. If students would be required to draw a bicycle, the difficulty of representing the mechanical parts itself could be taken as a point of departure for a discussion; if students would be required to explain verbally how the bicycle works, the drawing could be produced, in a guided way, to make it visible, step by step, the mechanical connections that make it possible for the vehicle to move. Our work presents various limits. Since the study concentrates only on the mechanism of the bicycle, it does not provide information on children’s ideas about other types of causal links. Aiming to the enrichment of BDT, we did not investigate if a verbal explanation produced in the absence of a drawing task presents the same shortcomings that children showed when talking about their drawing. Even in the perspective we adopted, age differences would be better studied in a longitudinal study. Also, the relations between mechanical reasoning and other aspects of intelligence remaines unsolved for future research. The modest correlation of the interview score with CPM prompts us to best investigate the relationship with other more complete intelligence measures. Acknowledgement The authors are grateful to the children who participated in this research. References Funding: This study was partially supported by Grant Ateneo 2016 from Sapienza, Rome Universit |
Cite this article as: Cannoni, E., Bombi, A. S., Marano, G., & Di Norcia, A. (2018). How does a bicycle work? A new instrument to assess mechanical reasoning in school aged children. Psicología Educativa, 24, 59-62. https://doi.org/10.5093/psed2018a10
Funding: This study was partially supported by Grant Ateneo 2016 from Sapienza, Rome University.
Correspondence: anna.dinorcia@uniroma1.it (A. Di Norcia).
Copyright © 2026. Colegio Oficial de la Psicología de Madrid








 e-PUB
e-PUB CrossRef
CrossRef JATS
JATS








