
Popularidad y relaciones entre iguales en el aula: un estudio prospectivo
[Popularity and peer relationships in the classroom: A prospective study]
Ignacio Ramos-Vidal1
1Univ. Sevilla, Fac. PsicologĂa, Dep. PsicologĂa Social, España
https://doi.org/10.1016/j.pse.2015.12.001
Resumen
Este artículo analiza la red de popularidad entre los compañeros de clase y la conexión que este fenómeno establece con diferentes tipos de relaciones (positivas, neutras y negativas) que se producen dentro del aula. Empleamos el Análisis de Redes Sociales (ARS) para identificar contextos de interacción en el aula. Evaluamos diferentes tipos de relaciones en 20 clases pertenecientes a dos centros de educación secundaria localizados en el área suburbana de la Ciudad de México. Participaron en total 660 estudiantes (67% mujeres, 33% varones), que proporcionaron los datos de la investigación. Calculamos los indicadores de cohesión para las redes positivas, neutras, negativas y de popularidad. Los análisis de clúster muestran dos perfiles basados en las propiedades estructurales de las redes que denominamos "simétrico neutro" y "asimétrico positivo". El primero presenta una distribución equilibrada entre sexos, baja homofilia y predominancia de relaciones neutras y positivas y el segundo muestra una distribución asimétrica de alumnos en función del sexo, elevada heterofilia y alta cohesión en relaciones positivas. Los análisis de regresión muestran que el número de alumnos por clase se relaciona de forma negativa con la densidad de la red positiva y de forma positiva con la densidad de la red negativa. La comparación simultánea de múltiples redes muestra que la popularidad se asocia con estar inmerso en relaciones positivas. Por el contrario los datos indican cierta incompatibilidad entre el hecho de ser popular y estar inmerso en relaciones negativas. Se discuten los hallazgos para mejorar la convivencia escolar y las políticas públicas en materia educativa
Abstract
This paper analyzes in depth the network of popularity among classmates and the connections that this phenomenon maintains with different kinds of relationships (i.e., positive, neutral, and negative) that take place within the classroom. We use Social Network Analysis (SNA) to identify interaction contexts in the classroom. Different kinds of relationships in 20 classrooms from two secondary schools located in the suburban area of Mexico City were assessed. The research data was provided by 660 students (67% girls; 33% boys). Cohesion measures were calculated for positive, neutral, negative, and popularity networks. Cluster analysis shows two profiles based on structural properties of the networks that we have called "Neutral Symmetric" and "Positive Asymmetric". The first one presents low homophily relative to sex, predominance of positive and neutral relationships, and a significant level of negative links. The second profile presents a heterogeneous distribution according to sex, high homophily and high rates of cohesion in positive relationships. Regression analysis shows that the number of students per class is negatively related to the positive network density, and positively related to the negative network density. The simultaneous comparison of multiple networks shows that popularity is associated with being immersed in positive relationships. By contrast, the data suggest certain incompatibility between being popular and being immersed in negative relationships. The findings are discussed in order to improve school life and public policies in education.
La evidencia empĂrica muestra que la adolescencia es una etapa en la que el grupo de pares desplaza parcialmente a la familia. En esta fase el grupo de iguales adquiere relevancia como contexto de socializaciĂłn en el que los jĂłvenes se sienten integrados, se perciben a sĂ mismos como sujetos con visiones similares de la vida, lo que hace más grata la experiencia de pertenencia al grupo ( Mortimer y Call, 2001 ). Sin embargo, el apego que experimentan los jĂłvenes respecto al grupo de iguales no implica que estas relaciones estĂ©n exentas de conflicto. Las dinámicas grupales en poblaciĂłn adolescente tambiĂ©n se caracterizan por el desacuerdo, la volatilidad de las relaciones, la alta rotaciĂłn de los intees del grupo y por las pugnas que se suscitan cuando algĂşn miembro pretende alcanzar mayor estatus ( Degirmencioglu, Urberg, Tolson y Richard, 1998 ).
Las interacciones que se producen en el contexto escolar con frecuencia se caracterizan por la ambigĂĽedad de rol y por la coexistencia de relaciones positivas, neutras y negativas, con capacidad de producir efectos diferenciales sobre el comportamiento grupal ( Huitsing et al., 2012 ). Este tema ha captado el interĂ©s de la comunidad cientĂfica y tradicionalmente ha sido infrainvestigado. Los mĂ©todos que examinan las interacciones grupales y la estructura que se deriva de estas relaciones (i.e., Análisis de Redes Sociales, ARS), se han centrado en evaluar relaciones de tipo positivo, como pueden ser el intercambio de informaciĂłn o los comportamientos colaborativos para el desarrollo de tareas ( Brass, Butterfield y Skaggs, 1998 ). Sin embargo existe un interĂ©s creciente por el análisis de vĂnculos negativos ( Everett y Borgatti, 2014 ). En los entornos educativos se ha prestado mayor atenciĂłn al estudio de las interacciones de carácter positivo, si lo comparamos con las investigaciones centradas en el análisis de vĂnculos negativos. Esto a pesar que los antecedentes disponibles demuestran que las escuelas son contextos potencialmente conflictivos ( Haynie, 2003; Juvonen, 2001). Witkow, Bellmor, Nishina, Juvonen y Graham (2005) encontraron que la tercera parte de una muestra de estudiantes de secundaria mantenĂa al menos un vĂnculo negativo con otro compañero del mismo centro. Este hallazgo induce a pensar que los contextos educativos pueden ser entornos tan conflictivos como cualquier otro espacio de interacciĂłn social. Debemos considerar que la adolescencia es un perĂodo crĂtico en el que los procesos de influencia dentro del grupo de iguales pueden verse agravados por las normas explĂcitas y tácitas que regulan el comportamiento en clase ( Jackson, Cappella y Neal, 2015 ). De otro lado, es necesario conocer en quĂ© medida el estatus percibido por los miembros del grupo (popularidad) se relaciona con el hecho de estar inmerso en redes que denotan vĂnculos positivos, neutros y negativos. Labianca y Brass (2006) afirman que las relaciones negativas pueden desplegar mayor capacidad que los vĂnculos neutros y positivos para modelar la estructura de los grupos sociales y el comportamiento de sus miembros. SegĂşn estos autores, los vĂnculos negativos que pueden generar mayor impacto son los que presentan las siguientes propiedades: a) reciprocidad, b) intensidad elevada, c) conciencia por parte de los actores de estar inmersos en una relaciĂłn conflictiva y d) existencia de un estatus diferencial entre las partes implicadas en el conflicto. Para comprender con mayor profundidad el marco teĂłrico de la investigaciĂłn, en el epĂgrafe siguiente presentamos el papel que juega la popularidad durante la adolescencia.
La popularidadLa necesidad de ser aceptado es un factor clave para comprender el comportamiento de los jóvenes, al mismo tiempo que alcanzar un nivel óptimo de popularidad se convierte en una finalidad en sà misma que se produce con el objetivo de adquirir un papel central en el grupo. Prinstein y Dodge (2008) señalan que los actores populares detentan poder y prestigio entre sus compañeros, pudiendo llegar a modificar las percepciones del grupo respecto a la norma social imperante, incrementando en consecuencia su capacidad de influencia social. Sin embargo el interés por lograr notoriedad en la escuela no opera de igual modo durante toda la etapa adolescente. Algunos autores, como Stone y Brown (1999) , señalan que la preocupación por ser popular en la escuela alcanza su punto álgido en los estudiantes de noveno grado 1 1
El grado equivalente en el sistema educativo español serĂa 3° y 4° de la ESO, mientras que en el sistema educativo mexicano, paĂs donde se ha desarrollado el estudio, corresponderĂa al tercer año de secundaria (14-16 años aproximadamente).
. Este hallazgo es coincidente con el de otros estudios que muestran que la transiciĂłn entre niveles educativos, es un momento crucial en el que los estudiantes se adaptan a un nuevo entorno y deben desarrollar diversas estrategias relacionales para posicionarse favorablemente en el nuevo contexto ( Cillessen y Rose, 2005; Lafontana y Cillessen, 2002 ). Por tanto no podemos hablar de un proceso estable, sino de un ciclo que varĂa a lo largo del tiempo. Esto supone que el nivel de popularidad produce efectos diferenciales a lo largo de la adolescencia, tanto en lo referente a la capacidad de influir sobre el grupo de iguales como a la susceptibilidad para ser influido por actores prestigiosos ( Aral y Walker, 2012). En este sentido, Allen, Porter, McFarland, Marsh y McElhaney (2005) muestran que la elevada susceptibilidad se asocia a lo largo del tiempo con problemas de ajuste psicosocial tales como depresiĂłn, ansiedad y estrĂ©s. Estos resultados parecen demostrar que los estudiantes que presentan bajos niveles de popularidad y aquellos que son abiertamente rechazados pueden experimentar mayores problemas emocionales y dificultades en la transiciĂłn hacia la vida adulta en comparaciĂłn con los alumnos socialmente integrados.La literatura centrada en las relaciones entre el grupo de pares distingue entre popularidad “percibida” y “sociomĂ©trica” ( Cillessen y Rose, 2005 ). Algunos autores señalan que se trata de diferentes dimensiones del estatus o del rango entre iguales ( Parkhurst y Hopmeyer, 1998 ). La popularidad percibida suele evaluarse a travĂ©s de la descripciĂłn cualitativa que aportan los miembros del grupo ( Adler y Adler, 1998 ). La popularidad sociomĂ©trica emplea un sistema de nominaciones entre los miembros del grupo para determinar el estatus de cada intee 2 2
Para una explicación de cómo se calcula el estatus sociométrico de cada miembro del grupo véase el estudio de Cillessen y Rose (2005).
. El empleo de tĂ©cnicas cuantitativas para evaluar la popularidad sociomĂ©trica es relativamente reciente, a excepciĂłn de los estudios que analizan el nĂşmero de nominaciones emitidas y recibidas para calcular el prestigio o la prominencia de un actor dentro del grupo. Una de las ventajas de este procedimiento es que permite obtener una puntuaciĂłn individual para medir el estatus de un sujeto dentro de un determinado colectivo. Sin embargo para analizar la estructura de un grupo social de manera agregada (p. ej., los alumnos de una clase), es decir, siendo el grupo la unidad de análisis, es necesario emplear tĂ©cnicas de ARS que difieren de las anteriormente citadas.Dentro del ARS se consideran tres niveles de análisis que se denominan a) diádico, b) egocĂ©ntrico y c) sociocĂ©ntrico ( Mizruchi y Marquis, 2006; Ramos-Vidal, 2015; Ramos-Vidal y Ricaurte, 2015 ). Las investigaciones a nivel diádico examinan las caracterĂsticas de las redes en funciĂłn de las vĂnculos que mantienen cada par de actores (diada). Los estudios egocĂ©ntricos analizan el conjunto de vĂnculos que un actor determinado (ego), mantiene con el resto de miembros (alteri) de su red. En los estudios egocĂ©ntricos los investigadores diseñan una serie de preguntas que se denominan generadores de nombres y que sirven para que el sujeto entrevistado (ego) pueda identificar a los alteri que componen su estructura relacional. En las investigaciones egocĂ©ntricas los investigadores desconocen a priori la identidad de los alteri que integran la red. Finalmente, las investigaciones a nivel socio-cĂ©ntrico (red completa) evalĂşan la estructura de relaciones que tiene lugar entre un conjunto definido de actores. La principal diferencia entre las investigaciones egocĂ©ntricas y socio-cĂ©ntricas es que en este Ăşltimo tipo son los investigadores quienes establecen los lĂmites formales de la red. Lo habitual es que la pertenencia a un grupo social sea la que determine los lĂmites de la red, como por ejemplo los alumnos de una clase, los participantes en un programa de intervenciĂłn o los estudiantes de un centro escolar.
El análisis estructural ha desarrollado numerosas tĂ©cnicas para evaluar redes completas o socio-cĂ©ntricas ( Marsden, 2002 ). En este trabajo utilizamos un diseño de investigaciĂłn socio-cĂ©ntrico porque nuestro interĂ©s primario es el grupo, a diferencia de la popularidad percibida en la que se analiza el fenĂłmeno desde un plano individual. En los Ăşltimos años se ha demostrado que el ARS y en particular el análisis socio-cĂ©ntrico son mecanismos efectivos para comprender la conexiĂłn entre los niveles micro y macro, haciendo posible integrar de manera natural ambas perspectivas ( Jackson et al., 2015 ). Esto se produce debido a que el ARS se fundamenta en el principio de interdependencia ( Mitchell, 1969 ), que asume que el comportamiento, y la posiciĂłn que ocupa un actor en un grupo social, se ve influido por la estructura de vĂnculos en la que está inmerso y vice-versa. En esta investigaciĂłn se analiza la popularidad a nivel de la red completa (clase) y se efectĂşa un análisis exploratorio para conocer la conexiĂłn que este fenĂłmeno establece con diferentes tipos de relaciones (positivas, neutras y negativas).
Que tengamos constancia, existen pocas investigaciones que hayan evaluado la popularidad en el contexto escolar a nivel socio-cĂ©ntrico y que además analicen al mismo tiempo diferentes tipos de relaciones. Uno de estos ejemplos es la contribuciĂłn de Huitsing et al. (2012) , que muestra que cuando se analizan mĂşltiples relaciones de manera simultánea, estas son interdependientes entre sĂ, es decir, que la posiciĂłn que un actor ocupa en un tipo de red (p. ej., positiva), determina el lugar que ese mismo actor ocupa en otro tipo de red (p. ej., negativa). A continuaciĂłn presentamos los objetivos de la investigaciĂłn.
ObjetivosEn el presente trabajo se analizan mĂşltiples tipos de relaciones entre adolescentes, utilizando como unidad de análisis las interacciones que se producen en el aula y evaluando los efectos que estas relaciones producen en el nivel de popularidad de los actores. A partir de este marco de referencia se proponen tres objetivos especĂficos:
Objetivo 1 . Caracterizar los procesos relacionales, evaluando cuatro tipos diferentes de relaciones que tienen lugar en la clase: positivas, neutras, negativas y popularidad. Empleamos como variables de análisis los indicadores de cohesiĂłn que nos proporciona el ARS para conocer las propiedades estructurales de las redes completas, siendo la unidad de análisis el salĂłn de clase. Mediante este primer objetivo se pretende establecer una tipologĂa de escenarios de interacciĂłn en el aula y caracterizarlos en base a las medidas de estructura y composiciĂłn de las distintas redes evaluadas. Dentro de este primer objetivo tambiĂ©n se persigue conocer el impacto que determinadas caracterĂsticas de las clases (p. ej., el nĂşmero de alumnos) ejercen sobre la cohesiĂłn de las redes evaluadas.
Objetivo 2 . Observar si existen conexiones entre el nivel de popularidad y estar inmerso en relaciones positivas, neutras y negativas. La hipótesis de partida que emplearemos, siguiendo los hallazgos de Labianca y Brass (2006) , es que las relaciones negativas establecerán una mayor asociación con la red de popularidad que las relaciones positivas y neutras.
Objetivo 3. C onocer la contribuciĂłn individual de las relaciones positivas, neutras y negativas sobre el grado de popularidad de los participantes. Este objetivo cumple la funciĂłn de ofrecer informaciĂłn relativa al posible proceso de dependencia que puede darse cuando se analizan mĂşltiples relaciones de manera conjunta.
Método ParticipantesEn total participaron en la investigación 660 estudiantes, distribuidos en dos centros educativos. En la primera escuela (Centro 1) participaron 409 estudiantes repartidos en once clases, de los cuales 134 eran varones (32.8%) y 275 mujeres (67.2%). En esta primera escuela, la edad media de los participantes era 15.55 años ( DT = 0.99, R = 8). En la segunda escuela (Centro 2) participaron en total 251 estudiantes pertenecientes a nueve clases, de ellos 83 eran varones (33.1%) y 166 mujeres (66.7%), habiéndose registrados dos casos perdidos (0.8%). En este segundo centro, la edad media de los encuestados era de 15.49 años ( DT = 1.04, R = 8). Si consideramos los datos de forma agregada, en total hemos analizado las relaciones en 20 clases y la distribución de la muestra completa en función del sexo indica la participación de 441 mujeres (67%) y 217 varones (33%).
ProcedimientoLos datos utilizados en esta investigación provienen de un estudio que se realizó en dos centros educativos públicos situados en dos zonas suburbanas del área metropolitana de la Ciudad de México. El protocolo de investigación fue en primer lugar aprobado por miembros del comité de ética de la institución promotora del estudio. Posteriormente, intees del equipo de investigación se reunieron con el personal directivo de los centros para presentarles los objetivos y el alcance de la investigación, asà como el protocolo previamente aprobado por parte de la universidad. La dirección de los centros colaboró durante todas las fases del proyecto. El equipo de investigación se comprometió a entregar al final del proceso un informe destinado a mejorar la calidad del servicio prestado por el centro y a socializar los resultados de la investigación con la comunidad educativa. Los estudiantes cumplimentaron los cuestionarios en clase en horario escolar. Durante la aplicación estuvo presente un miembro del equipo de encuestadores previamente adiestrados, que solucionaron las posibles dudas surgidas durante la cumplimentación. Los estudiantes tardaron entre 45 y 60 minutos en completar el cuestionario. La fase de trabajo de campo se extendió desde septiembre de 2013 hasta finales de noviembre del mismo año.
InstrumentoEn primer lugar es preciso describir el método desarrollado para obtener las cuatro redes correspondientes a otros tantos tipos de relaciones evaluadas. Le presentamos a cada estudiante el listado completo con los nombres de todos los compañeros de su clase 3 3
El cuestionario empleado en el estudio está disponible bajo petición al autor y también puede consultarse un modelo similar en el Anexo I de la siguiente obra ( Ramos-Vidal, 2015).
. A continuaciĂłn les pedimos que nominasen a los compañeros con los que mantenĂan relaciones positivas, neutras o negativas. Para evitar ambigĂĽedades a la hora de caracterizar cada tipo de relaciĂłn, el equipo de encuestadores ofreciĂł orientaciones a los alumnos para que pudiesen señalar cada relaciĂłn de forma unĂvoca. Les presentaron ejemplos para facilitar la identificaciĂłn de relaciones positivas (p. ej., ofrecer apoyo afectivo), neutras (p. ej., indiferencia, desinterĂ©s) y negativas (p. ej., antipatĂa, desconfianza). Posteriormente se les pidiĂł que asignaran a cada uno de sus compañeros un valor en funciĂłn del nivel de popularidad (siendo 1 = nada popular, 2 = algo popular y 3 = muy popular). Esto nos permitiĂł construir en el software Ucinet 6.3 ( Borgatti, Everett y Freeman, 2002 ) las matrices de adyacencia correspondientes a los cuatro tipos de relaciones (popularidad, positiva, neutra y negativa) exploradas en las 20 clases. La base completa de los análisis fueron en total 80 matrices de adyacencia. Análisis de datosCada objetivo formulado requiere seguir un procedimiento de análisis especĂfico. Para llevar a tĂ©rmino el objetivo inicial, en primer lugar se calcularon diferentes medidas de cohesiĂłn para las cuatro redes. Los indicadores seleccionados han sido utilizados previamente para evaluar relaciones entre adolescentes en contextos escolares (e.g., Brechwald y Prinstein, 2011; Huitsing et al., 2012 ). Empleamos el programa Ucinet 6.3 ( Borgatti et al., 2002 ) para calcular las medidas de cohesiĂłn y posteriormente trasladamos los indicadores a SPSS para la ejecuciĂłn de análisis posteriores. En la tabla 1 describimos los indicadores empleados en el primer objetivo especĂfico. Una vez calculados los parámetros de cohesiĂłn, efectuamos un análisis de conglomerados a travĂ©s del procedimiento de las K-medias ( Kaufman y Rousseeuw, 2009 ), al objeto de identificar diferentes perfiles de las aulas, que estuviesen determinados en funciĂłn de las medidas de estructura y composiciĂłn de las redes analizadas.
DescripciĂłn de los indicadores de cohesiĂłn
| Indicador | DescripciĂłn |
|---|---|
| Tamaño de clase | Indica el número de alumnos que hay en cada clase. Para calcular todos los indicadores las puntuaciones han sido normalizadas al objeto de evitar desviaciones derivadas del número de alumnos por clase. |
| ĂŤndice de paridad | El Ăndice de paridad (Ip) refleja el equilibrio en la proporciĂłn de hombres y mujeres en cada clase. Los valores oscilan entre 1 y 2. Cuanto más prĂłximo a la unidad, existe mayor equilibrio entre ambos sexos, siendo 1 el punto de máximo equilibrio que refleja una composiciĂłn equivalente del 50% de hombres y de mujeres. Cuanto más se aproxime a 2, muestra una composiciĂłn más descompensada, siendo 2 el punto donde el 100% de los alumnos es del mismo sexo. La expresiĂłn matemática utilizada para calcular este indicador es la siguiente, donde N t es el nĂşmero total de alumnos de clase y N m representa el nĂşmero de mujeres: Ip=Nt2xNm2 |
| Homofilia (sexo) ( Krackhardt y Stern, 1988; McPherson, Smith-Lovin y Cook, 2001 ) | Este indicador se evalĂşa a travĂ©s del Ăndice E-i. Refleja el grado en que los actores del mismo sexo tienden a establecer relaciones con otros actores del mismo sexo. Los valores del Ăndice E-i oscilan entre -1 (cuando los actores sĂłlo establecen relaciones con personas de su mismo sexo, lo que reflejarĂa un alto grado de homofilia) y 1 (en el caso en que los actores sĂłlo establecen relaciones con personas del sexo opuesto, lo que reflejarĂa un alto grado de heterofilia). Valores prĂłximos a 0 indican una distribuciĂłn equilibrada de relaciones entre los grupos en funciĂłn del atributo de referencia (el sexo en este caso). |
| Homofilia (edad) ( Krackhardt y Stern, 1988; McPherson et al., 2001 ) | Muestra el grado en que los actores de la misma edad tienden a establecer relaciones con otros actores de edad equivalente. TambiĂ©n se evalĂşa a travĂ©s del Ăndice E-i. Los valores de este indicador oscilan entre -1 (cuando los actores sĂłlo establecen relaciones con personas de la misma edad, lo que reflejarĂa un alto grado de homofilia) y 1 (en el caso en que los actores sĂłlo establecen relaciones con personas de distinta edad, lo que estarĂa indicando un alto grado de heterofilia). Valores prĂłximos a 0 indican una distribuciĂłn equilibrada de relaciones entre los grupos diferenciados en funciĂłn del atributo de referencia (la edad en este caso). |
| Densidad (Harary, 1969) | ProporciĂłn de contactos que tiene lugar en una red, en relaciĂłn al total de vĂnculos posibles. Este indicador se interpreta a modo de porcentaje donde un valor de 0.61 indica que en una red tienen lugar el 61% de relaciones posibles. Se calcula dividiendo el nĂşmero de vĂnculos (L), por el nĂşmero de arcos posible g (g-1). ?=Lgg-1 |
| Reciprocidad | Muestra el grado en que los vĂnculos emitidos por los actores son correspondidos. Al igual que la densidad, esta medida se interpreta a modo de porcentaje donde un valor de 0.55 indica que el 55% de las relaciones que se producen en una red son recĂprocas o simĂ©tricas. |
| NĂşmero lazos | Indica el nĂşmero total de vĂnculos que se producen en una red social. |
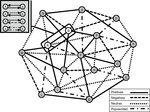
La consecuciĂłn del segundo objetivo exige un procedimiento especĂfico. Para evaluar la existencia de asociaciones entre las matrices positivas, neutras y negativas y la matriz de la red de popularidad, utilizamos el Procedimiento de AsignaciĂłn Cuadrática [Quadratic Assignment Procedure, QAP]. Esta tĂ©cnica permite comparar matrices de adyacencia utilizando un test de permutaciones no paramĂ©trico entre las diadas que componen la red ( Krackhardt, 1988). La figura 1 ilustra el análisis de las redes tomando como unidad básica la diada. La imagen trata de representar de modo visual cĂłmo cada diada que forma parte de un mismo grupo puede estar conectada mediante diferentes tipos de lazos que son susceptibles de ser evaluados de forma independiente.
El procedimiento QAP se utiliza en el ARS como alternativa a los procedimientos estadĂsticos tradicionales, debido en parte a la imposibilidad de garantizar la independencia de las observaciones en datos relacionales. El cálculo de correlaciones diádicas tambiĂ©n se llevĂł a cabo con el programa Ucinet 6.3. En primer lugar, la funciĂłn de correlaciĂłn QAP computa el coeficiente de correlaciĂłn de Pearson ( r ) entre las celdas correspondientes de las dos matrices. En un segundo paso permuta filas y columnas de una de las matrices de forma sincrĂłnica y al azar, calculando nuevamente la correlaciĂłn. La permutaciĂłn se lleva a cabo cientos de veces para computar la proporciĂłn de ocasiones en las que una correlaciĂłn al azar es mayor o igual a la correlaciĂłn observada en el primer paso, de tal modo que una proporciĂłn baja (menor que .05) sugiere una relaciĂłn fuerte entre las matrices que es poco probable que se deba al azar ( Borgatti et al., 2002; Krackhardt y Stern, 1988 ). Para efectuar los análisis dicotomizamos previamente las redes de popularidad como paso necesario antes de calcular la densidad y la reciprocidad, puesto que de no hacerlo podrĂamos obtener valores en ambos indicadores superiores a 1 (equivalente al 100%).
Para calcular la correlación QAP se introdujo como número máximo de permutaciones 2500 y como número de iniciación aleatorio 1000. Tomamos esta decisión para evitar posibles desviaciones derivadas del procedimiento de extracción ( Krackhardt, 1988 ). Se empleó la matriz de la red de popularidad (que es introducida como la primera matriz, denominada observada ) y de los distintos tipos de relaciones (positivas, neutras y negativas). A este respecto Kwon y Lease (2014) señalan que en términos de la magnitud de la correlación QAP los valores correspondientes al valor r de Pearson que oscilan entre .1 y .3 muestran una correlación pequeña, los valores comprendidos entre .3 y .5 indican una correlación moderada, mientras que los valores por encima de .5 reflejan una correlación elevada.
Para el tercer objetivo empleamos nuevamente el procedimiento QAP, pero en esta ocasiĂłn efectuamos regresiones mĂşltiples (MRQAP). Esta tĂ©cnica consiste en incluir varias matrices que actĂşan como variables independientes de forma simultánea ( Krackhardt, 1993 ). Empleamos la opciĂłn conocida como Double Semipartialling (DSP), porque permite un mayor ajuste del modelo de regresiĂłn en análisis de interdependencia a nivel diádico ( Dekker, Krackhardt y Snijders, 2007 ). Esta rutina de análisis es adecuada cuando existen elevados niveles de colinealidad entre las matrices analizadas ( Dekker et al., 2007 ). Empleamos esta tĂ©cnica porque los análisis de colinealidad entre el principal indicador de cohesiĂłn (densidad) de las distintas redes mostrĂł valores moderadamente elevados en el factor de inflaciĂłn de la varianza (FIV) y en el grado de tolerancia (T). DespuĂ©s de calcular los coeficientes de los modelos de regresiĂłn, trasladamos los datos a SPSS para obtener los estadĂsticos descriptivos ( M y DT). En la figura 2 se describen los objetivos de la investigaciĂłn y la metodologĂa empleada para cumplir cada uno de ellos.
Resultados Objetivo 1El primer objetivo pretende establecer una tipologĂa de contextos de interacciĂłn en el aula, empleando como variables de categorizaciĂłn varios de los indicadores de cohesiĂłn descritos en la tabla 1 . Para conocer los valores de estos indicadores y las posibles diferencias entre los dos centros educativos que conforman la muestra, en la tabla 2 presentamos los estadĂsticos descriptivos identificando los valores promedios de la muestra completa y tambiĂ©n diferenciando los valores obtenidos en ambos centros.
EstadĂsticos descriptivos de los indicadores de cohesiĂłn para las redes positiva, neutra, negativa y de popularidad
| Indicador | Muestra | MĂnimo | Máximo | M | DT |
|---|---|---|---|---|---|
| Tamaño clase | Agregada | 21 | 47 | 32.95 | 7.83 |
| Centro 1 | 26 | 47 | 36.60 | 8.04 | |
| Centro 2 | 21 | 34 | 27.78 | 3.66 | |
| ĂŤndice de paridad | Agregada | 1.06 | 2 | 1.51 | .31 |
| Centro 1 | 1.06 | 1.58 | 1.32 | .19 | |
| Centro 2 | 1.23 | 2 | 1.74 | .29 | |
| Homofilia (sexo) | Agregada | -1.0 | -.021 | -.32 | .36 |
| Centro 1 | -.38 | .02 | -.12 | .14 | |
| Centro 2 | -1.0 | -0.13 | -.60 | .39 | |
| Homofilia (edad) | Agregada | -.47 | .61 | .03 | .27 |
| Centro 1 | -.47 | .16 | -.13 | .20 | |
| Centro 2 | -.01 | .61 | .26 | .18 | |
| Densidad red positiva | Agregada | .33 | .88 | .60 | .21 |
| Centro 1 | .33 | .51 | .42 | .05 | |
| Centro 2 | .78 | .88 | .82 | .03 | |
| Reciprocidad red positiva | Agregada | .34 | .80 | .55 | .14 |
| Centro 1 | .34 | .50 | .43 | .05 | |
| Centro 2 | .66 | .80 | .61 | .04 | |
| NĂşmero lazos red positiva | Agregada | 286 | 1116 | 611.8 | 237.21 |
| Centro 1 | 286 | 1116 | 591.80 | 305.66 | |
| Centro 2 | 335 | 910 | 626 | 164.78 | |
| Densidad red neutra | Agregada | .06 | .49 | .28 | .17 |
| Centro 1 | .37 | .49 | .43 | .04 | |
| Centro 2 | .06 | .14 | .10 | .03 | |
| Reciprocidad red neutra | Agregada | 0 | .45 | .22 | .15 |
| Centro 1 | .25 | .45 | .35 | .05 | |
| Centro 2 | 0 | .11 | .06 | .04 | |
| NĂşmero lazos red neutra | Agregada | 44 | 867 | 362.7 | 311.39 |
| Centro 1 | 287 | 867 | 579.10 | 225.21 | |
| Centro 2 | 44 | 163 | 76.56 | 38 | |
| Densidad red negativa | Agregada | .03 | .19 | .10 | .04 |
| Centro 1 | .11 | .18 | .13 | .02 | |
| Centro 2 | .03 | .12 | .07 | .03 | |
| Reciprocidad red negativa | Agregada | .01 | ,24 | .10 | .07 |
| Centro 1 | .08 | .24 | .15 | .05 | |
| Centro 2 | .01 | .08 | .04 | .02 | |
| NĂşmero lazos red negativa | Agregada | 26 | 348 | 133.2 | 99.82 |
| Centro 1 | 77 | 309 | 183.80 | 77.65 | |
| Centro 2 | 26 | 107 | 56.11 | 26.38 | |
| Densidad red popularidad | Agregada | .28 | .91 | .63 | .13 |
| Centro 1 | .49 | .71 | .62 | .06 | |
| Centro 2 | .28 | .91 | .63 | .19 | |
| Reciprocidad popularidad | Agregada | .16 | .85 | .46 | .16 |
| Centro 1 | .27 | .56 | .43 | .09 | |
| Centro 2 | .16 | .85 | .48 | .22 | |
| NĂşmero lazos popularidad | Agregada | 246 | 1546 | 746.05 | 362.77 |
| Centro 1 | 506 | 1546 | 912.50 | 359.22 | |
| Centro 2 | 246 | 702 | 504.89 | 187.97 |
Como podemos observar en la tabla 2 , existen diferencias en los indicadores de cohesiĂłn entre los dos centros educativos. Algunas de estas diferencias es lĂłgico que se den, puesto que en el caso del tamaño de la clase existen diferencias estadĂsticamente significativas entre ambos contextos y este indicador se relaciona positivamente con el nĂşmero de vĂnculos que se producen en los cuatro tipos de relaciones evaluadas. Por este motivo decidimos no emplear como variables de agrupaciĂłn en el análisis de conglomerados ni el tamaño de la clase ni el nĂşmero de vĂnculos existentes en los cuatro tipos de relaciones examinadas. De igual modo no incluimos en este análisis ningĂşn indicador de reciprocidad, puesto que esta medida tambiĂ©n se relaciona con la densidad y elegimos incluir sĂłlo esta Ăşltima como variable de agrupaciĂłn por su potencial explicativo. En la tabla 3 presentamos los resultados del análisis de conglomerados.
Análisis de clúster indicando los centros finales de los conglomerados
| Indicadores de cohesiĂłn | Conglomerado 1 (n = 12) | Conglomerado 2 (n = 8) |
|---|---|---|
| Centros finales | Centros finales | |
| ĂŤndice de paridad | 1.32 | 1.81 |
| Homofilia basada en el sexo (red de popularidad) | -.11 | .73 |
| Homofilia basada en la edad (red de popularidad) | -.08 | .25 |
| Densidad de la red positiva | .45 | .82 |
| Densidad de la red neutra | .41 | .10 |
| Densidad de la red negativa | .13 | .07 |
Nota . El procedimiento ha convergido en dos iteraciones.
Los resultados indican la existencia de una soluciĂłn Ăłptima de dos conglomerados. El primer subgrupo, el más numeroso, está compuesto por doce clases, mientras que el segundo clĂşster incluye ocho aulas. La primera agrupaciĂłn presenta: a) un valor moderado en el Ăndice de paridad que indica una composiciĂłn equitativa de las clases en funciĂłn del sexo, b) el nivel de homofilia basada en el sexo (Ăndice E-i) está prĂłximo a cero, lo que indica la existencia de relaciones equilibradas entre ambos sexos, c) tambiĂ©n se observa la misma tendencia en el grado de homofilia en funciĂłn de la edad, que refleja el establecimiento de relaciones mixtas con compañeros de distintas edades y d) finalmente si prestamos atenciĂłn a la cohesiĂłn, encontramos un nivel intermedio de densidad en las redes positivas (45%) y neutras (41%), mientras que la densidad de la red negativa es moderadamente alta (13%).
El panorama que muestra el segundo conglomerado es diferente. Los centros finales del segundo clĂşster presentan: a) un nivel exiguo del Ăndice de paridad, que indica la existencia de clases en las que la composiciĂłn es homogĂ©nea, b) el nivel de heterofilia en funciĂłn del sexo es elevada (.73), lo que refleja que en este contexto los estudiantes mantienen mayoritariamente relaciones con actores del sexo opuesto 4 4
Debemos mencionar que el nivel de homofilia (tanto basada en el sexo como en la edad) corresponden a la red de popularidad por lo que dicha tendencia de asociaciĂłn se circunscribe a ese tipo de relaciĂłn.
, (c) si examinamos el valor del Ăndice E-i relativo a la edad, observamos una tendencia de menor magnitud hacia la heterofilia (.25), que indica que entre los participantes existe predisposiciĂłn a establecer conexiones con estudiantes de diferentes edades y (d) por Ăşltimo, al examinar los valores correspondientes a los tres indicadores de cohesiĂłn, podemos ver que se da un nivel elevado de densidad en las relaciones positivas (82%) y reducidos en la densidad de las redes neutras (10%) y negativas (7%).Una vez descritas las propiedades de los dos subgrupos identificados, podemos señalar que cada clĂşster representa un perfil diferenciado en base a los parámetros de estructura y composiciĂłn. Hemos denominado al primer perfil “simĂ©trico neutral” mientras que el segundo perfil ha sido nombrado “asimĂ©trico positivo”. El perfil simĂ©trico neutral refleja una composiciĂłn equitativa en la proporciĂłn de mujeres y varones que componen el aula, e indica un bajo nivel de homofilia en base al sexo (-.11) y a la edad (-.08) en la red de popularidad. Al mismo tiempo, exhibe un entorno relacional neutro, en el que se adivina un nivel moderado de cohesiĂłn en la red negativa 5 5
Si bien un 13% puede parecer un valor moderado en la densidad de relaciones negativas, estudios previos (e.g., Kossinets y Watts, 2006 ) señalan que en las redes negativas los parámetros de cohesión suelen presentar valores muy por debajo de los que muestran las redes neutras y positivas.
. Al contrario, el perfil asimĂ©trico positivo muestra un desequilibrio evidente en la composiciĂłn de los miembros de la clase y un alto grado de heterofilia en funciĂłn del sexo (.73). Sin embargo, las clases que conforman este conglomerado presentan un nivel de cohesiĂłn elevado en las relaciones positivas, lo que denota un clima saludable. Posteriormente decidimos realizar una serie de análisis ad hoc para indagar en estos resultados. A nivel exploratorio efectuamos las correlaciones entre el tamaño de la clase (excluida del análisis de clĂşster), el Ăndice de paridad y el nivel de densidad de las redes positivas, neutras y negativas. En la tabla 4 se muestran los resultados.Correlaciones entre una selecciĂłn de indicadores de cohesiĂłn evaluados
| Indicadores de cohesiĂłn | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1. Tamaño de la clase | -- | |||||
| 2. ĂŤndice de paridad | -.470 * | -- | ||||
| 3. Densidad red de popularidad | -.021 | .235 | -- | |||
| 4. Densidad red positiva | -.570 ** | .557 * | -.003 | -- | ||
| 5. Densidad red neutra | .549 * | -.634 ** | -.053 | -.982 ** | -- | |
| 6. Densidad red negativa | .533 ** | -.215 | .255 | -.832 ** | -.740 ** | -- |
p < .05.
p < .01.
Podemos apreciar que el tamaño de clase correlaciona de forma inversa y al máximo nivel de significaciĂłn con la densidad de la red positiva. Simultáneamente el tamaño de la clase correlaciona en sentido positivo con la densidad de la red negativa. Por su parte el Ăndice de paridad mantiene conexiones con la densidad de las distintas redes. Este indicador presenta una relaciĂłn de covarianza con la densidad de la red positiva. Adicionalmente llevamos a cabo tres análisis de regresiĂłn mĂşltiple para conocer el efecto conjunto que ejercen el Ăndice de paridad y el tamaño de la clase (que actĂşan como independientes) sobre la densidad de las redes positivas, neutras y negativas (que actĂşan como dependientes en cada modelo). En los tres modelos se comprobĂł que no existen problemas de colinealidad (observado mediante el FIV y T) ni de autocorrelaciĂłn entre los residuos (evaluado a travĂ©s del contraste de Durbin-Watson).
El resumen del primer modelo de regresiĂłn en el que la variable dependiente es la densidad de relaciones positivas ( R 2 = .432, ?R 2 = .365, F = 6.467, p = .008), indica que el nĂşmero de alumnos se relaciona negativamente (? = -.396) con la densidad de vĂnculos positivos, mientras que el Ăndice de paridad tiene un efecto similar (? = .371), señalando que a menor paridad, es decir, cuanto más homogĂ©neas son las clases, se da una mayor proporciĂłn de relaciones positivas. El resumen del segundo modelo, en el que la densidad de relaciones neutras actĂşa como dependiente ( R 2 = .483, ?R 2 = .422, F = 7.929, p = .004), señala que el tamaño de la clase incide positivamente sobre la densidad de relaciones neutras (? = .322); por su parte el Ăndice de paridad ejerce una notable influencia en la densidad de vĂnculos neutros, de modo que cuanto mayor equilibrio existe en la composiciĂłn de las clases en funciĂłn del sexo, hay un mayor nĂşmero relaciones neutras (? = -.483). Los resultados del tercer modelo de regresiĂłn en el que la densidad de relaciones negativas ejerce de dependiente ( R 2 = .285, ?R 2 = .201, F = 3.394, p = .058), no es estadĂsticamente significativo, pero parece indicar que el nĂşmero de estudiantes por clase incide de forma notable sobre la densidad de vĂnculos negativos (? = .554). Esto supone que cuanto mayor es el tamaño de la clase, existe una mayor proporciĂłn de vĂnculos negativos. En este modelo el Ăndice de paridad (? = .046) apenas explica la varianza de la densidad de relaciones negativas. Estos resultados muestran que el nĂşmero de alumnos por aula y la distribuciĂłn por sexo dentro de la clase influyen de forma particular sobre la densidad de relaciones positivas y neutras y en menor medida tambiĂ©n en la densidad de vĂnculos negativos.
Objetivo 2Para conocer las posibles asociaciones que las redes positivas, neutras y negativas mantienen con la red de popularidad, llevamos a cabo mĂşltiples correlaciones a nivel diádico siguiendo el procedimiento QAP ( Krackhardt y Stern, 1988 ). Estos análisis fueron efectuados en las 20 clases evaluadas. Posteriormente se trasladaron los resultados a SPSS para calcular los estadĂsticos descriptivos ( M y DT). En la tabla 5 6
En todos los casos la primera matriz que aparece en la columna inicial de la tabla 5 es la observada mientras que la segunda es la matriz de estimaciĂłn.
exponemos la media y la desviaciĂłn tipo del nivel de correlaciĂłn del coeficiente r de Pearson y del grado de significaciĂłn ( p).Media y desviaciĂłn tĂpica del coeficiente de correlaciĂłn de Pearson ( r ) y del nivel de significaciĂłn ( p ) entre la red de popularidad y las redes positivas, neutras y negativas
| Matrices correlacionadas 6 | Muestra | Coeficiente r de Pearson | Nivel de significaciĂłn (p) | ||
|---|---|---|---|---|---|
| M | DT | M | DT | ||
| Red de popularidad y red positiva | Agregada | .256 | .139 | .024 | .050 |
| Centro 1 | .271 | .089 | .005 | .016 | |
| Centro 2 | .237 | .188 | .048 | .067 | |
| Red de popularidad y red neutra | Agregada | -.102 | .121 | .142 | .177 |
| Centro 1 | -.147 | .092 | .096 | .162 | |
| Centro 2 | -.047 | .135 | .200 | .187 | |
| Red de popularidad y red negativa | Agregada | -.176 | .204 | .069 | .114 |
| Centro 1 | -.117 | .098 | .041 | .067 | |
| Centro 2 | -.249 | .276 | .104 | .151 | |
Los datos indican que existe una asociaciĂłn pequeña (dentro del rango comprendido entre .1 y .3) entre la red de popularidad y la red positiva ( r = .257), siendo estas correlaciones en promedio estadĂsticamente significativas ( p = .024). Las correlaciones entre la red de popularidad y las redes neutras y negativas no presentan valores significativos en la muestra agregada. Sin embargo, si prestamos atenciĂłn a los datos correspondientes al Centro 1 (conformado por 11 clases), podemos apreciar que existe una covariaciĂłn inversa entre la red de popularidad y la red de vĂnculos negativos ( r = -.117, p = .041). Por otro lado, si observamos los valores de la desviaciĂłn tipo, se aprecia una amplia variabilidad entre las clases de ambos centros. Aunque los resultados evidencian que existe conexiĂłn entre el grado de popularidad a nivel de cada clase y el desarrollo de relaciones positivas, no se cumple el pronĂłstico que efectuamos siguiendo a Labianca y Brass (2006) , dado que las correlaciones son sensiblemente inferiores entre la red de popularidad y la red negativa en comparaciĂłn con la red positiva. Sin embargo la correlaciĂłn entre la matriz de popularidad y la red neutra es inferior que la registrada entre la matriz de popularidad y la red negativa.
Objetivo 3El último objetivo se propuso para conocer en qué medida las relaciones positivas, neutras y negativas, que actúan como independientes, explican de manera conjunta el nivel de popularidad (que cumple la función de dependiente). Llevamos a cabo un modelo de regresión diádica múltiple (MRQAP) entre las diferentes redes de las 20 clases. Posteriormente trasladamos los resultados a SPSS para calcular la media y la desviación tipo de los coeficientes de los 20 modelos calculados. La tabla 6 recoge la media y la desviación tipo del coeficiente ? estandarizado de las redes positivas, neutras y negativas y la media y desviación tipo de los resúmenes de los 20 modelos de regresión efectuados.
Media y desviaciĂłn tĂpica de los valores de los modelos QAP de regresiĂłn mĂşltiple entre la red de popularidad y las redes positivas, neutras y negativas para la muestra agregada ( n = 20 clases)
| Matrices Indep. | Matriz dependiente Red de popularidad | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ? (estand.) | Sign. (p) | Error est. | R 2 | ?R 2 | Prob. | |||||||
| M | DT | M | DT | M | DT | M | DT | M | DT | M | DT | |
| Positiva | .367 | .469 | .026 | .097 | .061 | .020 | ||||||
| Neutra | .155 | .556 | .069 | .121 | .224 | .121 | .166 | .215 | .163 | .216 | .001 | .006 |
| Negativa | .030 | .429 | .138 | .154 | .221 | .102 | ||||||
Podemos apreciar que la matriz de relaciones positivas es la que produce un mayor efecto sobre el nivel popularidad, mostrando un efecto moderadamente elevado en promedio (? = .367, p = .024). Las matrices neutras presentan menos capacidad en promedio que las positivas (? = .155, p = .069) para explicar la varianza de la red de popularidad, mientras que las matrices negativas apenas muestran una contribuciĂłn simbĂłlica (? = .030, p = .118) para explicar la varianza de la popularidad.
DiscusiĂłnA lo largo del manuscrito hemos presentado la importancia del grupo de pares durante la adolescencia, prestando especial atenciĂłn a las relaciones que tienen lugar en la escuela como contexto socializador. Uno de los propĂłsitos de este artĂculo es identificar una tipologĂa de contextos de interacciĂłn en el salĂłn de clase. Para ello utilizamos como variables de agrupaciĂłn indicadores estructurales (p. ej., densidad) y a continuaciĂłn examinamos la asociaciĂłn entre el grado de popularidad y el establecimiento de relaciones positivas, neutras y negativas. Se emplearon datos de carácter socio-cĂ©ntrico, que fueron proporcionados por 660 estudiantes distribuidos en 20 clases de dos centros educativos.
Hemos utilizado el ARS a nivel socio-céntrico, seleccionando como unidad de análisis la clase. Las técnicas socio-céntricas ofrecen una imagen más concisa de la estructura de relaciones en el aula, lo que hace posible identificar a los actores más populares y además permite conocer la configuración estructural de la clase en función del tipo particular de relación explorada.
En segundo lugar se han evaluado de manera simultánea diferentes tipos de relaciones (positivas, neutras y negativas). Las investigaciones que examinan el estatus y los procesos de influencia social en adolescentes analizan el impacto del estatus sobre comportamientos desviados ( Allen et al., 2005 ) o bien sobre comportamientos prosociales ( Ryan, 2000 ), siendo poco habitual encontrar estudios que combinen ambos enfoques ( Ellis y Zarbatany, 2007).
La tercera contribuciĂłn es establecer las asociaciones que existen entre los distintos tipos de relaciones (positivas, neutras y negativas) y el modo en que estas influyen sobre la popularidad dentro del aula. Utilizamos el procedimiento QAP para testar las correlaciones (objetivo 2) y las relaciones de dependencia (objetivo 3), entre la red de popularidad y las redes positivas, neutras y negativas. El Ăşnico antecedente encontrado en el que se aplica esta tĂ©cnica, es la reciente propuesta de Kwon y Lease (2014) , en la que los autores emplean este procedimiento para identificar asociaciones entre los estudiantes del mismo curso. Nuestro diseño difiere del anterior en que nosotros examinamos las relaciones a nivel de clase, al considerar que las dinámicas relacionales y los procesos de influencia social alcanzan su máxima expresiĂłn en el aula, debido a que las relaciones se intensifican y existe una elevada proximidad fĂsica.
A travĂ©s del análisis de clĂşster identificamos dos perfiles diferenciados que hemos denominado “simĂ©trico neutral” y “asimĂ©trico positivo”. El primer perfil describe clases en las que hay: a) equilibrio en la composiciĂłn entre hombres y mujeres, b) bajos niveles de homofilia en funciĂłn del sexo, c) predominancia de relaciones positivas y neutras de cohesiĂłn moderada y d) cierta densidad relacional negativa, lo que puede ser el sĂntoma de un clima conflictivo en el aula. El segundo perfil representa a clases que se caracterizan por mostrar: a) una composiciĂłn desproporcionada entre hombres y mujeres, b) un alto nivel de heterofilia basada en el sexo, c) un nivel elevado de cohesiĂłn en las relaciones positivas y d) un bajo grado de densidad en las relaciones neutras y negativas. Esta configuraciĂłn parece describir un entorno relacional saludable.
Los análisis diseñados ad hoc para conocer el impacto del tamaño de la clase y del Ăndice de paridad sobre el grado de cohesiĂłn de las relaciones positivas, neutras y negativas muestran que ambos factores (tamaño y distribuciĂłn en funciĂłn del sexo) son elementos que contribuyen a explicar los procesos relacionales en el aula. Los hallazgos apuntan a que el nĂşmero de alumnos por clase se asocia en sentido negativo con la densidad de relaciones positivas (? = -.396) e inversamente con el Ăndice de paridad (? = .371). Estos resultados parecen indicar que en las clases de mayor tamaño, y en las que hay una composiciĂłn equitativa de chicos y chicas, nos encontramos con menor densidad en las redes positivas. Por otro lado la asociaciĂłn negativa entre el tamaño de clase y la densidad de relaciones positivas puede explicarse parcialmente debido a que a mayor nĂşmero de alumnos se incrementa el nĂşmero de subgrupos que componen el aula. Cuantas más agrupaciones cohabiten en el aula, es probable que entren en contraposiciĂłn los intereses de cada una, posibilitando un aumento de los conflictos tanto individuales como intergrupales.
Por otro lado encontramos una potente asociaciĂłn entre el Ăndice de paridad y la densidad de relaciones neutras (? = -.483). Este dato sugiere que cuanto más equilibrada sea la composiciĂłn entre mujeres y varones en el aula existe mayor cohesiĂłn en relaciones carentes de contenido o indiferentes. Esto quizás se deba a que a esas edades hay menor coincidencia en los temas de discusiĂłn y en las preocupaciones que suelen predominar en ambos sexos ( Giordano, 2003 ). TambiĂ©n observamos que el tamaño de la clase mantiene una potente conexiĂłn con la densidad de vĂnculos negativos (? = .554). Este resultado sugiere que los incrementos en el nĂşmero de alumnos por clase hacen que concurran las circunstancias para que se den relaciones negativas entre los miembros del grupo. Es posible que este hecho se relacione con las dificultades que pueden encontrar los docentes para mantener un clima orientado a la tarea en clases excesivamente pobladas.
Estos resultados avalan la tendencia actual de apostar por clases cada vez más reducidas que faciliten el proceso de enseñanza-aprendizaje. Los análisis aquĂ presentados parecen indicar que las dinámicas relacionales que se producen en clases pequeñas, en las que hay un alto grado de homogeneidad en funciĂłn del sexo, describen contextos en los que predominan las relaciones positivas. Esta informaciĂłn puede ser tenida en consideraciĂłn por gestores y diseñadores de polĂticas pĂşblicas en materia educativa, con el objetivo de generar ambientes positivos que faciliten el desarrollo integral del alumnado.
Los dos siguientes objetivos examinaban la relaciĂłn entre la red de popularidad y las redes positivas, neutras y negativas. Para ello utilizamos correlaciones y regresiones QAP, que permiten conocer el nivel de asociaciĂłn entre las redes. Siguiendo las directrices de Labianca y Brass (2006) , propusimos como hipĂłtesis complementaria que las relaciones negativas presentarĂan un mayor nivel de asociaciĂłn y dependencia en comparaciĂłn con las relaciones positivas y neutras. Se identificĂł una correlaciĂłn positiva entre la red de popularidad y la red positiva ( r = .256), siendo además la Ăşnica correlaciĂłn que presenta valores significativos para la muestra agregada ( p = .024). Estos resultados parecen reflejar que para los jĂłvenes la popularidad se asocia principalmente al hecho de estar inmerso en relaciones positivas, que por lo general denotan comportamientos prosociales. TambiĂ©n observamos una asociaciĂłn inversa entre el nivel de popularidad y la participaciĂłn en relaciones negativas ( r = -.176), aunque en este caso las correlaciones no son estadĂsticamente significativas ( p = .069). Este dato sugiere cierta incompatibilidad entre el hecho de ser popular y estar inmerso en relaciones negativas pero, considerando el nivel de significaciĂłn estadĂstica, debe ser interpretado con cautela. Sin embargo estos hallazgos no permiten soportar la hipĂłtesis de que las relaciones negativas cuentan con mayor capacidad que las positivas y que las neutras para definir la estructura de la red de popularidad.
Los hallazgos son prometedores en tanto que la literatura muestra que los actores populares tienen mayor capacidad que los rechazados y que los no populares para generar influencia social y actuar como modelos positivos de conducta. Esta contribución puede ayudar a diseñar estrategias de intervención en las que los actores populares actúen como promotores de cambio, por ejemplo colaborando como facilitadores en programas orientados a mejorar la convivencia y el desempeño académico. La incorporación de este tipo de estrategias en el diseño de intervenciones socio-educativas puede incrementar el impacto y la validez ecológica de la intervención ( Carr et al., 2002).
El análisis en profundidad de las dinámicas relacionales que tienen lugar en los contextos educativos exige desarrollar nuevas perspectivas de investigaciĂłn. La continuidad de esta lĂnea se orientará a proponer estrategias de intervenciĂłn estructural ( Valente, 2012 ), con el objetivo de introducir modificaciones en la estructura de las redes que se producen en el aula (p. ej., promoviendo la interacciĂłn entre ciertos grupos), tendentes a mejorar el clima escolar, a facilitar la integraciĂłn de los actores aislados y a conducir procesos de influencia social positivos.
LimitacionesNuestros datos proceden de dos escuelas, por lo que las prácticas educativas y las polĂticas institucionales podrĂan estar condicionando las dinámicas relacionales en las clases de ambos centros. Por otro lado, los dos centros evaluados están radicados en entornos suburbanos, donde existe una alta concentraciĂłn de poblaciĂłn. En este sentido, como apuntan Kwon y Lease (2014) , serĂa necesario incrementar el nĂşmero de centros participantes y realizar estudios comparativos en centros situados en zonas rurales y metropolitanas, al objeto de observar si las caracterĂsticas del contexto en el que se asienta la escuela pueden influir en las relaciones que el alumnado establece en el aula. En segundo lugar, debemos acotar con mayor exactitud el significado que los jĂłvenes asignan al hecho de ser “popular”. La mayor parte de estudios que analizan el nivel de popularidad basado en el estatus sociomĂ©trico no ofrecen una definiciĂłn previa del concepto, considerando que el significado del tĂ©rmino es una nociĂłn consensuada entre los adolescentes. Sin embargo algunas propuestas, como las desarrolladas por Lafontana y Cillessen (2002) , muestran que para los jĂłvenes la popularidad se asocia tanto a comportamientos pro-sociales como disruptivos. Finalmente, nuestros datos son de carácter transversal, por lo que teniendo en consideraciĂłn la volatilidad que caracteriza a las relaciones afectivas durante la adolescencia ( Brechwald y Prinstein, 2011 ), es necesario desarrollar investigaciones longitudinales para conocer con mayor profundidad la evoluciĂłn temporal que experimentan los adolescentes tanto en el nivel de popularidad como en los procesos de influencia social que de este fenĂłmeno se derivan.
Extended SummaryAdolescence is a critical period in the emotional development process. During this stage of the vital cycle, young people should adapt to new contexts where the influence of the peer group gradually gains strength if we compare it with the capacity to modify the behavior exerted by parents and extended family until this moment ( Ryan, 2000 ). For this reason it is necessary to pay special attention to the adaptation process of child at school, and in particular to the construction of relationships among peers within the classroom. Although it is well known that adolescents are highly influenced by their classmates, less is known about the types of relationships that have greater potential to affect the behavior. From this perspective, it is considered that perceived popularity and sociometric status are key factors to understand the relational patterns among peers ( Cillessen & Rose, 2005).
However, in the academy there is no clear consensus on whether popularity is associated with being immersed in positive, neutral, or negative relationships ( Ellis & Zarbatany, 2007 ). Therefore, it is also unknown whether students relate popularity with prosocial or disruptive behaviors, and how popularity, along with different types of relationships, can be used to establish structural or relational profiles in the classroom. The main objective of this paper is bridging the existing gap, generating specific knowledge that helps us to understand these questions: (a) what are the structural properties which enable us to categorize the classrooms according to the characteristics of the links that connect classmates? (b) how are group features (i.e., group size) influencing positive, neutral, and negative relationships? and (c) what kinds of relationships among peers are associated with being popular? To address theses questions we use Social Network Analysis (SNA) and a set of methods designed to compare multiples relationships – networks – at the same time ( Dekker, Krackhardt, & Snijders, 2007; Krackhardt, 1988 ). For this purpose a cross-sectional study was developed. The research data was provided by 660 students (67% girls, 33% boys), with an average age of 15.5 ( SD = 1.01) who belonged to 20 classrooms from two secondary schools located in a suburban area of Mexico City. We decided to the classroom as a unit of analysis in contrast to previous research (e.g., Kwon & Lease, 2014 ) that d the social networks at the grade level. This decision was taken because students spend most of school time in the classroom, and hence it is likely that the relational processes that we want to assess are most evident at the classroom level, where the relationships are more intense and closer.
We designed a social network instrument to evaluate different types of relationships (i.e., popularity, positive, neutral, and negative) among peers in the classroom. A self-administered socio-centric questionnaire ( Marsden, 2002; Ramos-Vidal, 2015 ) was used to elicit the social networks of the classrooms. The instrument s a matrix in which the rows contained the names of all the classmates, and the columns displayed the four types of relationships evaluated. Students should nominate the classmates with whom they establish each of the relationships mentioned above. Afterwards, the information was introduced in Ucinet 6.3 ( Borgatti, Everett, & Freeman, 2002 ), a software to relational data that serves to calculate social network structural measures. For each of the 20 classrooms we obtained four different networks corresponding to the four kinds of relationships evaluated, giving a total of 80 social networks (adjacency matrices) for all the classrooms involved in the study. To identify relational contexts, we calculate structural properties for each network. The main structural measures evaluated were: density (which reflects the degree of network cohesion), homophily (the tendency of people to maintain connections with other people with whom they have features in common), and reciprocity (that indicates the proportion of ties that are symmetrical). Once the indicators for all the networks were calculated, the next step was to enter the measures in SPSS for further analysis. Cluster analysis was used to categorize the 20 classrooms based on the structural measures. This analysis allows us to identify profiles of classrooms focused on a set of properties determined by the researchers ( Kaufman & Rousseeuw, 2009).
Cluster analysis showed two profiles that we have called Neutral Symmetric and Asymmetric Positive. The first one ( n = 12 classrooms) presented low homophily relative to sex, predominance of positive and neutral relationships, and a significant level of negative links. The second profile ( n = 8 classrooms) presents a heterogeneous distribution according to sex, high homophily and high rates of cohesion in positive relationships (see Table 3 ). These findings suggest that the management practice at school and the distribution of students regarding to sex and age, impact on the classroom climate in terms of the particular kinds of relationships that take place in each profile identified. We also develop multiple regression analyses to know the influence promoted by two features of the classrooms (group size and distribution of classrooms according to sex) on the cohesion of the relationships evaluated. The analyses yielded the following results: (a) group size is negatively related (? = -.396) with the density of positive relationships, while an equal distribution of alumni regarding to sex is positively related (? = .371); (b) group size is positively (? = .322) associated with the cohesion of neutral relationships; (c) finally, group size shows a powerful effect (? = .554) on the cohesion of negative relationships, so that the larger size classes may report more negative ties. These results suggest that the number of students per class, and in a lesser degree, the distribution of students according to sex are influencing on the cohesion of the relationships studied.
To address the second objective of this paper, we use a method which makes it possible to simultaneously two or more networks. The technique known as Quadratic Assignment Procedure (QAP) was used to test the association between networks. In this case, we used first the QAP to compute the correlations between all the relationships evaluated (see Table 5 ). In second place, we develop a multiple regression QAP model (MRQAP) to know the impact of positive, neutral, and negative matrices on the popularity network (see Table 6 ). For the correlation analysis, the algorithm proceeds in two steps. In the first step, it computes Pearson's correlation coefficient ( r ) between corresponding cells of the two matrices. In the second step, it randomly permutes rows and columns (synchronously) of one matrix and recomputes the correlation and other measures. The second step is carried out hundreds of times in order to compute the proportion of times that a random measure is larger than or equal to the observed measure calculated in step 1. A low proportion (< .05) suggests a strong relationship between the matrices that is unlikely to have occurred by chance. For the MRQAP analysis, in the first step the algorithm compute a regression instead a correlation and the second step is the same as for correlation ( Borgatti et al., 2002; Dekker et al., 2007; Krackhardt, 1993; Krackhardt & Stern, 1988 ).
Our findings a positive (r = .256) and significant (p = .024) QAP correlation between popularity and positive networks. The results that for young people popularity is mainly associated with being immersed in positive relations which usually denote prosocial behavior. In contrast, an inverse association between the level of popularity and the participation in negative relationships was observed ( r = -0.176). This data suggests certain incompatibility between being popular and being immersed in negative relationships in the classroom.
The contributions of this paper should help to design intervention strategies in which popular students serve as inducers of positive change within the classroom and in the peer group. For example, taking part in programs designed to improve the academic performance of disadvantage students. Finally, the application of SNA to looking inside the classroom dynamics can be considered a powerful research tool capable of connecting the micro and macro levels, but is essential to complement this information with a detailed knowledge of educational practices and policies implemented by schools.
FinanciaciĂłnEsta investigaciĂłn ha sido financiada parcialmente por la SecretarĂa de EducaciĂłn PĂşblica del Gobierno de MĂ©xico, a travĂ©s de los Fondos PROMEP (Proyecto 13412093).
Conflicto de interesesEl autor del artĂculo declara que no tiene ningĂşn conflicto de intereses.
Copyright © 2025. Colegio Oficial de la Psicología de Madrid









 CrossRef
CrossRef








