Oversimplifying Teaching of the Control of Variables Strategy

Introduction

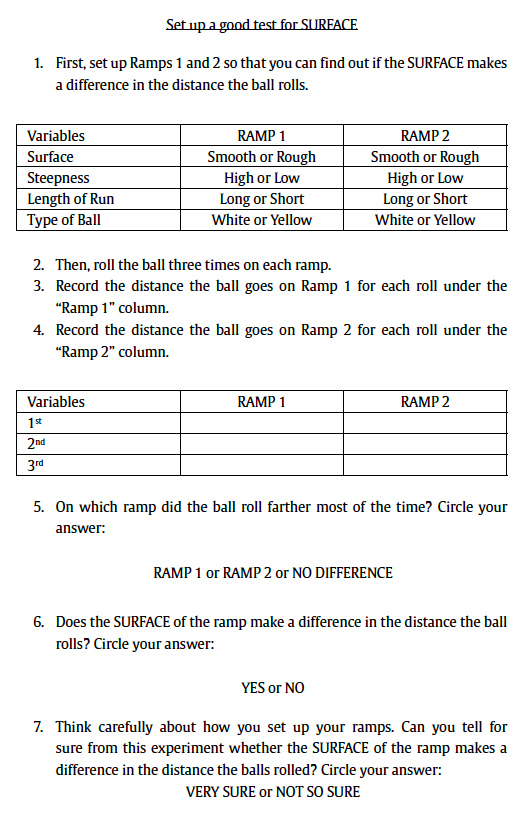
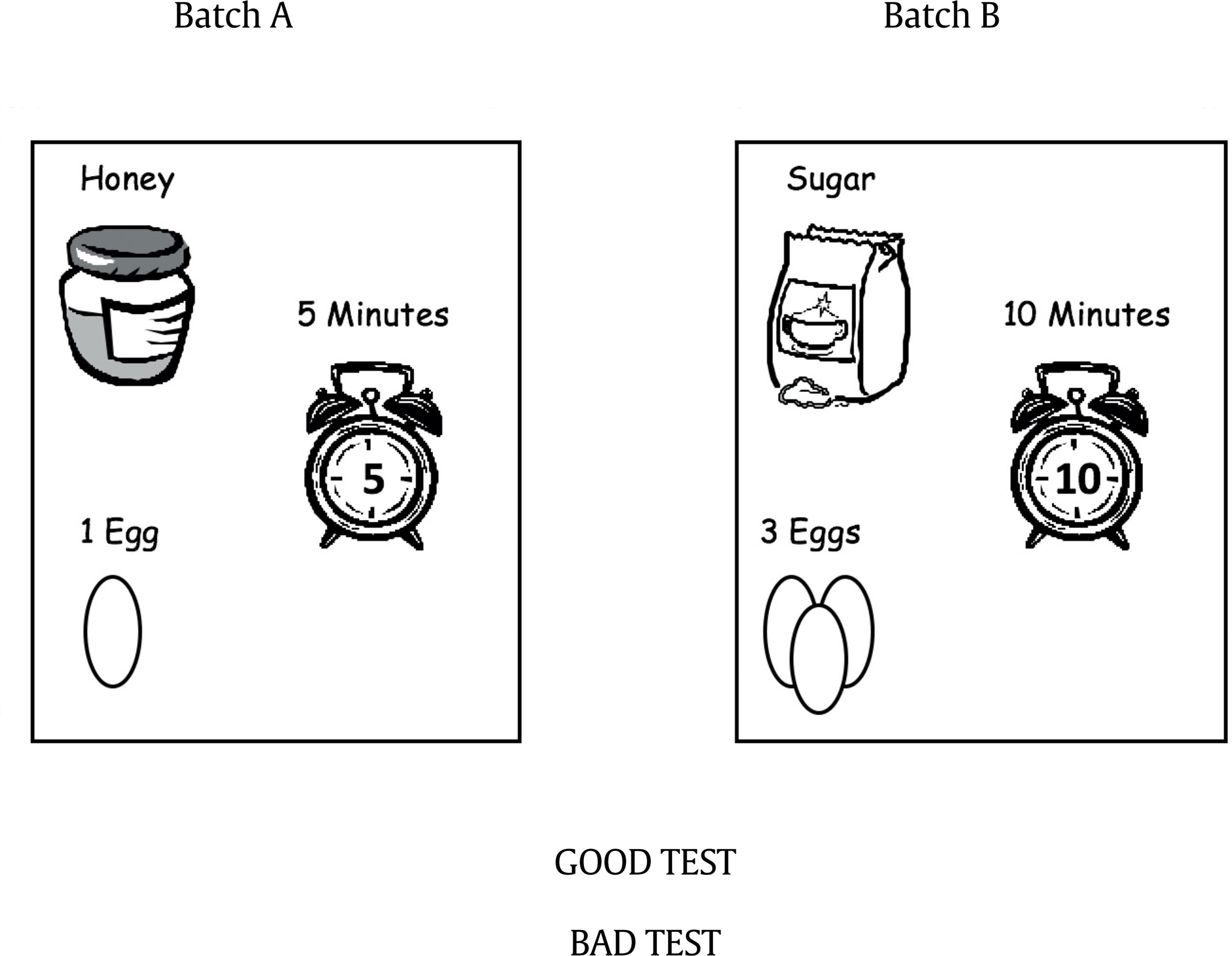
A literate person must have a basic understanding of how science works. One important component of scientific literacy is understanding that the ability to identify causal relations between variables is central to explaining scientific phenomena and, in turn, that isolating causal relations depends on being able to control irrelevant variables. Indeed, an understanding of the logic of controlling variables is a landmark goal of early science education (National Research Council, 1996; Zimmerman, 2005).

Instruction in strategies to control variables (CVS) has been the focus of a great deal of education research (Ross, 1988; Schwichow, Croker, Zimmerman, Hoffler, & Hartig, 2016) and the subject of a long debate in the literature. There continues to be much discussion of the relative merits of embedding instruction of CVS in an authentic, complex scientific context (Allchin, 2014; Kuhn, Ramsey, & Arvidsson, 2015) as opposed to teaching CVS in a simpler and relatively isolated scientific context (Klahr & Chen, 2011; Lorch et al., 2014). This discussion should and will continue; however, there is now substantial empirical evidence that a rudimentary understanding of CVS can be effectively taught to many 4^th-grade students using a relatively brief intervention that emphasizes direct instruction of the key concepts.

A protocol first developed by Chen and Klahr (1999) has proven effective at teaching CVS in lab studies. The basic teaching intervention uses a simplified, concrete domain to illustrate the logic of experimentation. For example, a commonly used domain investigates the effects of different variables on how far a ball rolls down a ramp. Two ramps are compared that can be varied on any of four, binary variables: the height of the ramp (high or low); the starting point for rolling the ball (long or short “length of run”); the surface of the ramp (rough or smooth); and the color of the ball (yellow or white). The student is initially shown a comparison of the two ramps that confounds all four variables and is asked whether the comparison is a good test (i.e., valid comparison) of whether one specific variable (i.e., the focal variable) affects how far a ball will roll. Most students say that the comparison is a good one but regardless of the student’s response, the experimenter then quizzes the student on the potential effect of each individual variable. This discussion leads to the conclusion that because each of the variables might affect how far the ball rolls, the proposed test is not a good one because it will not be able to distinguish an effect of the focal variable from the possible effects of the other variables. Rather, a good comparison is one in which the two ramps differ only in the value of the focal variable. The student and experimenter then reconfigure the ramps to produce a valid test of the focal variable. This entire interchange is repeated with a new, confounded example of an experiment to help the student consolidate an understanding of the principle that in order to construct a valid test of a focal variable, the values of the focal variable must differ while the values of the other three variables must be kept the same. This intervention has proven more effective in teaching CVS than alternative methods in which students are allowed to explore the experimental domain and construct comparisons but are not given such direct instruction in how and why to manipulate the focal variable while holding all other variables constant in value (Chen & Klahr, 1999; Klahr & Nigam, 2004; Strand-Cary & Klahr, 2008; Triona & Klahr, 2003).

The teaching intervention developed by Chen and Klahr (1999) in the lab has been successfully adapted to classroom instruction essentially by making the interchange between the instructor and students a classroom conversation rather than an individual conversation (Lorch et al., 2010; Toth, Klahr, & Chen, 2000). In addition, testing of students’ competence at constructing experiments and evaluating experimental comparisons in new domains is modified for group testing by having students take more responsibility for recording their responses. In 30 minutes of classroom instruction of CVS, higher achieving students (Zohar & Aharon-Kravetsky, 2005; Zohar & Peled, 2008) and students from higher-achieving schools (Lorch et al., 2010; Lorch et al., 2014) show good immediate understanding of how to construct new experiments in the learning domain and are good at evaluating the validity of experimental comparisons in new domains. Further, learning is retained well throughout the school year (Chen & Klahr, 1999; Klahr & Nigram, 2004; Lorch et al., 2010; Lorch et al., 2014; Strand-Cary & Klahr, 2008; Triona & Klahr, 2003) and has been shown to be retained as long 2.5 years later (Lorch et al., 2017).

Despite the impressive success in high-achieving schools of the intervention developed by Chen and Klahr (1999), the same intervention has produced positive but less impressive outcomes for lower-achieving students (Zohar & Aharon-Kravetsky, 2005; Zohar & Peled, 2008) and students in lower-achieving schools (Lorch et al., 2010; Lorch et al., 2014). This pattern is not an uncommon one in education (Cronbach & Snow, 1977) but its basis has not been identified. It is likely the consequence of multiple factors. In the case of lower-achieving students, poor cognitive skills might contribute to low efficacy of a teaching intervention (Fuchs, 2014; German, 1999; Orton, McKay, & Rainey, 1964; Osier & Trautman, 1961). In the case of lower-achieving schools, little exposure to the domain may reduce the effectiveness of the intervention (Lorch et al., 2010; Lorch et al., 2014). In practice, of course, it is extremely difficult to separate the contributions of deficiencies in students’ cognitive skills from school failings with respect to providing adequate educational opportunities.

Whether the unimpressive outcomes for students in lower-achieving schools are attributable to a high proportion of students who are cognitively challenged or a general lack of familiarity with the domain, a possible strategy for improving the outcomes of CVS instruction is to simplify instruction. There are several ways this might be accomplished: by further constraining the problem domain, by providing cognitive supports to the students, and/or by attempting to simplify the procedure taught for controlling irrelevant variables in a domain. All three of these approaches were investigated in this study.

We report two experiments that modify the basic teaching intervention developed by Chen and Klahr (1999). In Experiment 1, we compared Chen and Klahr’s intervention to an analogous intervention in which the learning environment was simplified by reducing the number of irrelevant variables the students had to consider (i.e., from three to one irrelevant variables). In addition, we provided students with an additional cognitive support of a booklet designed to systematically guide their planning of experiments at testing. The rationale for both modifications of the intervention was to reduce the cognitive demands of the learning and testing situations. If Chen and Klahr’s intervention imposes too great a load on the cognitive capacities of this student population, the modifications of the intervention should produce better learning of CVS.

In Experiment 2, we compared the Chen and Klahr’s (1999) protocol for teaching CVS to a modification of the protocol that provided an easier way to achieve control of irrelevant variables. Instead of instructing students to decide on a variable-by-variable basis whether to have the values of a variable differ or stay the same as in Chen and Klahr’s procedure, the modified protocol instructed students to initially set the values of each variable equal, then identify the focal variable and change one of its values. Again, the rationale is that the modified procedure for achieving control of variables is less cognitively demanding than Chen and Klahr’s original procedure so it should lead to better student performance if the cognitive demands of the original procedure are the source of the unimpressive learning of this student population.

If the cognitive demands of Chen and Klahr’s (1999) intervention are the source of its lower efficacy with students who are lower-achieving or from lower-achieving schools, then the modified interventions in Experiments 1 and 2 should result in improved learning. On the other hand, there also is reason to predict that Chen and Klahr’s intervention will produce better learning than the simplified protocols. Empirically, we previously have found that Chen and Klahr’s intervention produced better learning than a closely matched intervention that reduced variability in the types of examples used to teach the logic of CVS (Lorch et al., 2014). This was the case despite the fact that the less variable set of examples produced more consistency with respect to illustrating the attributes of a valid experimental design. Theoretically, simplifying a teaching context by providing a simpler rule can encourage rote learning (Schwartz, Chase, Opprezzo, & Chin, 2011) and simplifying a teaching context by placing greater constraints on the context can cause students to fail to make important distinctions between concepts or situations (Feldman, 2003; Gomez, 2002; Hahn, Bailey, & Elvin, 2005). Both consequences can lead to learning that is relatively fragile and so it is poorly retained and does not transfer well to new situations (Koedinger, Corbett, & Perfetti, 2012).

Experiment 1

A full understanding of the control of variables strategy requires that a student understand that: (a) the goal of an experiment is to isolate the effect of a single variable; (b) there must be different values of the focal variable (i.e., the focal variable must be manipulated); and (c) the influences of other variables must be eliminated by holding constant the values of all irrelevant variables. In addition, the student must know how to implement each of these intentions concretely when designing or evaluating an experiment. The Chen and Klahr’s (1999) intervention teaches the logic of CVS in a constrained domain where just four variables with only two values each are explicitly identified for the student and the goal of a given experiment is always to investigate the effect of just one of the four variables. Despite the relatively simple experimental environment, a novice in science may experience a heavy load on working memory when trying to design an experiment. If that is the case, it should be possible to facilitate students’ learning by lessening the demands on memory.

In Experiment 1, we investigated two factors that should help students manage memory demands in the learning situation. First, we manipulated whether students had a booklet to guide and record their planning of an experimental design when conducting ramps experiments. This external memory aid should help students both to systematically plan their experiments and to reduce the amount of information they must hold in working memory at any point during the planning and set up of the experiment. The practice at designing several experiments with such an aid may also translate into better understanding of the attributes of a valid experiment.

The second factor manipulated in Experiment 1 was the number of variables in the learning domain. We compared learning in a domain with four specified variables to learning in the same domain but with only two variables specified. If students struggle to understand CVS because the memory demands are too great, reducing the number of variables should facilitate learning. On the other hand, a potentially negative effect of reducing the number of variables is that it reduces variability in the examples of valid and invalid designs to which students are exposed. This may interfere with learning the important distinctions between valid and invalid designs which, in turn, may limit students’ ability to generalize beyond the immediate learning situation (Feldman, 2003; Gomez, 2002; Hahn et al., 2005). For example, with only two variables to illustrate the concept of CVS, students may actually learn that “one factor must vary and one factor must not vary” and the choice of which to vary is dictated by which factor is designated as the focal variable. When a new variable is introduced or more than two variables must be considered, students may not know how to extend their rule to the new situation.

In sum, if the working memory demands of the Chen and Klahr’s (1999) teaching intervention are an important influence on learning, then learning should be aided by providing a planning booklet and/or reducing the number of variables to be considered. If the working memory demands in the Chen and Klahr protocol are manageable by students, then neither manipulation should affect learning and the reduction of the number of variables may even interfere with learning.

Method

Participants. The participants were 130 students attending public elementary schools that were classified as low-achieving on the state-mandated test of science achievement (Core Content for Science Assessment, 2006). All of the students were fourth graders who attended an afterschool program at their elementary school. Students were assigned at random to the four experimental conditions. Each student received $15 for participation. The students and their parent(s)/guardian(s) were all informed of the nature and purpose of the research and consented to participate under the condition that their individual results would be recorded without identifying information.

Materials. The materials consisted of instructional materials and materials for assessing learning. The instructional materials consisted of a pair of ramps; 2 white and 2 yellow golf balls; 2 carpet pieces that could be inserted into the ramp to create a smooth or rough surface; and a pair of blocks that served to elevate one end of each ramp (Figure 1). Each ramp was hinged in the middle and consisted of a smooth section that served as the “down ramp” that a ball could be rolled down and an “up ramp” with a series of numbered sections that slowed and eventually stopped a rolled ball. The ramps were used by the instructor in explaining the control of variables strategy. They also were used by participants to set up experimental comparisons as part of the procedure for assessing understanding of CVS.

In addition to the ramps materials, a planning booklet was created to guide students in designing and executing experiments with the ramps (Figure 2). The booklet included a page for each of four experiments that the students were to design. Each page specified a different variable to be tested, then provided a table that specified each of the four variables in the domain and allocated space for the students to indicate which value of each variable they selected for Ramp A and which value of each variable they selected for Ramp B in their design. Thus, the table helped students to systematically plan their experimental design and was available to them to refer to while setting up an experiment. The remainder of each page directed students to run three trials of the experimental comparison, record the results, state the trend, and conclude whether the focal variable had an effect on performance.

Finally, three parallel “comparison tests” were created to test students’ ability to evaluate the validity of experimental designs. The comparison tests consisted of 21 pages, each 8.5 x 11 inches. The first page was a cover page. The cover page was followed by a page that introduced a domain and established a goal (e.g., experimenting with a recipe for baking cookies in order to determine what produces the best-tasting cookies), then introduced 3 variables with 2 values each (e.g., number of eggs in the recipe was 1 or 3; type of sweetener was sugar or honey; baking time for the cookies was 5 or 10 minutes). A specific experimental comparison was then explained in words and illustrated in pictures and the student was asked to evaluate whether the comparison was a “good test” (i.e., valid comparison) of a specified focal variable. The student circled “good” or “bad” below the pictures to indicate his or her response (Figure 3). The following pages illustrated seven more comparisons testing the three variables multiple times for a total of eight comparisons. This half of the booklet was followed by a page instructing the student to “stop.” The remaining pages of the book introduced a new domain and eight more comparisons in the new domain, followed by a “stop” page.

Thus, the comparison tests constituted “far transfer” tests of students’ understanding of CVS because (a) they tested understanding in domains that were very different from the ramps domain of instruction and (b) they required evaluation of experimental comparisons rather than the construction of an experimental design. Across the 16-item test, six comparisons were valid comparisons (i.e., the two conditions being compared differed only with respect to the values of the focal variable), eight were confounded comparisons (four doubly confounded and four singly confounded), and two were noncontrastive comparisons in which only one of the three variables differed in value but the manipulated variable was not the focal variable (i.e., the comparison tested the wrong variable).

Design and Procedure. The experimental design was a 2 x 2 between-Ss design in which the factors were the number of variables in the learning domain (2 vs. 4) and whether students were provided with a planning booklet during the ramps test. There were four steps in the procedure: (1) the student completed a comparison test as a pretest of understanding of CVS; (2) the student received instruction according to the condition (i.e., 2 or 4 variables); (3) the student designed four ramps experiments as a test of understanding of CVS either using or not using a planning book, depending on the experimental condition; and (4) the student completed a second comparison test as a posttest of their understanding of CVS.

Each student participated individually in the experiment. In the first step of the procedure, the student was given one of the three comparison tests. The instructor explained the reason for the test and then read through the page introducing the first domain on the test. The instructor took care that the student understood the goal of the experiments illustrated in the test and could identify the three variables. The student completed the eight items for the first domain, then the instructor introduced the second domain and the student completed the eight items for the second domain.

In the second step of the procedure after completing the comparison pretest, the instructor introduced the student to the ramps domain and explained that the student was going to learn how to “make good experiments.” For the four-variable condition of the experiment, the variables in the domain were identified and the student was shown how to vary the two values of each variable. The concept of a “good experiment” was explained to the student: “An experiment is ‘good’ if it allows you to determine whether the variable you want to test is the only variable that could have influenced how far the ball rolled down the ramp.” The instructor then set up a completely confounded experiment with the ostensible purpose of testing whether the “length of run” variable (i.e., point at which the ball was released on the down ramp) influenced how far the ball rolled. The instructor ran this experimental comparison three times to show that the ball that started higher on the ramp did, indeed, go further. The experimenter then asked the student to think about why this result happened. The instructor had the student identify all the ways in which the two ramps set-ups differed (i.e., on all four variables) and evaluate for each variable whether the difference in values might affect how far the ball rolled. When the student recognized that all four variables differed and that each variable could influence performance, the instructor reminded the student of the variable they wanted to evaluate and then explained why it was bad that the comparison differed on all four variables. The instructor then guided the student to re-design the experiment so that it would be a good test of the Length of Run variable. This involved taking apart one of the ramps and considering the variables one-at-a-time, beginning with the focal variable. For each variable, the student was reminded of which variable they were testing and was asked whether the two values of the variable currently under consideration should be the same (“yes” for irrelevant variables) or different (“yes” for the focal variable). This sequence led to the construction of a new, valid comparison and concluded with an explicit statement of the control of variables strategy. Following completion of this portion of the instructional protocol, the whole sequence was repeated with a new focal variable in a design that was partially confounded (i.e., two of the four factors varied), once again correcting that to a valid design and concluding with the explicit statement of the control of variables strategy.

The teaching protocol for students assigned to the 2-variable domain referred only to the variables of Type of Surface and Length of Run. In all other respects, the teaching protocol was analogous to that for the 4-variable domain. The students were introduced to the domain in the same way as for the 4-variable domain, but only the variables of Surface and Length of Run were identified and illustrated. In developing the logic of CVS, the teaching protocol initially presented a test of Length of Run where the variable of Length of Run was confounded with the variable of Surface. In the second example of the protocol, the focal variable was Surface and the variable of Length of Run was confounded with it. The variables of Type of Ball and Steepness were never introduced at any point in the protocol. In all other respects, the 2-variable protocol was analogous to the 4-variable protocol.

In the third step of the procedure after the instructional protocol was completed, understanding of CVS was tested in two ways. First, the student was given the set of ramps and asked to conduct four experiments, one testing each of the variables in the domain. All students in the four-variable condition were tested on the variables in the same order: Length of Run, Surface, Steepness, Type of Ball. Half of the students were provided with a planning booklet to help guide them in designing and executing their experiments; half of the students did not receive a planning booklet so they were instructed to simply set up the ramps directly to construct each test rather than having the intermediate step of writing out their plan and using it to guide their ramps set up. To record the ramps tests performances of these students, the experimenter simply filled out a planning booklet as the student set up and ran the experiment. The number of valid experiments designed by a student was taken as an assessment of immediate transfer of learning of CVS as it reflected the student’s competence at doing the same task (i.e., designing experiments) in the same domain (i.e., ramps) in which they were instructed.

The students assigned to the 2-variable domain also conducted four ramps experiments after completing the teaching protocol. However, unlike the students in the 4-variable domain who conducted experiments on all four variables, these students only conducted experiments on the two variables from their learning domains. They were asked to test the variables in the order: Length of Run, Surface, Length of Run, Surface. Thus, all students designed ramps tests only for the variables they experienced during the teaching protocol. Again, half of the students were provided with a planning booklet and half were not.

In the final step of the procedure after completing the ramps test, the student was given a second comparison test identical in format and procedure to the pretest but differing in domains. The number of correct items on the comparison test assessed far transfer of learning because it evaluated understanding of CVS using a new task (i.e., evaluation of experimental comparisons) in domains different from the domain in which instruction occurred. The entire procedure typically took approximately 45 minutes to complete.

Results and Discussion

Separate analyses were conducted on the data from the ramps tests and the comparison tests. None of the students achieved mastery (≥ 85% correct) on the comparison pretest, so the data of all 130 students were included in both analyses. The level of significance adopted for all statistical tests was .05.

Ramps tests. The data for the ramps tests were analyzed in two ways: one analysis was on the number of valid experimental designs a student produced across the four tests and the other analysis was on the number of valid experimental designs a student produced for the test of the Surface and Length of Run variables (i.e., the two variables that were tested in both the 2-variable and 4-variable conditions); for this analysis, only the first tests of these variables were considered in the 2-variable condition. The pattern of results from the two analyses was identical, so only the results from the first analysis are reported.

The two variables in the ANOVA were the number of variables in the learning domain (2 vs. 4) and whether the student was given a planning book during the ramps test. Only the main effect of the number of variables was significant. Simplifying the experimental environment actually interfered with students’ learning of CVS: students in the 4-variable condition constructed more correct designs (M = 2.66, SD = 1.63) than students in the 2-variable condition (M = 1.92, SD = 1.63), F(1, 123) = 6.58, partial η² = .051. There was no evidence that the availability of a planning booklet helped students on the ramps test; in fact, students who did not have a booklet did slightly (M = 2.42, SD = 1.56) but not significantly better than students who did have a booklet (M = 2.16, SD = 1.76).

Comparison tests. The comparison test data were analyzed with a mixed-factors ANOVA in which the within-Ss factors were Test (pretest vs. posttest) and Item-type (valid, confounded, noncontrastive) and the between-Ss factors were Number of Variables (2 vs. 4) and Booklet (present vs. absent). There were two notable results from the analysis. First, the proportion correct responses varied across Item-types, F(2, 252) = 44.72, partial η² = .262. Performance was best on the valid items (M = .67) but much worse on the confounded items (M = .45) and noncontrastive items (M = .40). Unlike previous investigations (Lorch et al., 2010; Lorch et al., 2012; Lorch et al., 2017), the magnitude of the effect of Item-type did not depend significantly on any other factor. Second and most importantly, the improvement from pretest to posttest was greater in the 4-variable condition (M change = .16) than in the 2-variable condition (M change = .07), F(1, 126) = 4.11, partial η² = .032. The superiority of the 4-variable condition was also clear in an analysis of the posttest results for the proportion of students who achieved mastery: twice as many students achieved mastery in the 4-variable domain (M = .29, SE = .050) than in the 2-variable domain (M = .14, SE = .051), F(1, 126) = 4.17, partial η² = .032.

In sum, the key finding for both measures of CVS understanding were consistent in showing that students learned CVS better in the 4-variable domain than in the 2-variable domain. This was true both when the test assessed immediate transfer (i.e., the ramps test) and when the test assessed far transfer (i.e., the comparison test). There was no evidence that the availability of a planning booklet facilitated performance in the situation where it was used (i.e., the ramps test) or that it led to a better understanding of CVS as measured in the far transfer test. These results show that the limited learning by students in low-achieving schools demonstrated in prior studies (Lorch et al., 2010; Lorch et al., 2014) is not due to the cognitive demands of working with four variables.

The lack of effect of the manipulation of the availability of a planning booklet when designing and executing the ramps test is, perhaps, unsurprising. In the absence of a planning book, the students had an alternative memory support, namely, the ramps were visible and could be directly manipulated.

More interestingly, students benefitted more from learning in a domain with four variables than from learning in a domain with two variables. Although additional variables increase the memory load on students, this potential disadvantage was outweighed by other considerations. One of those considerations may have been that the presence of several irrelevant variables emphasized the general principle that the values of all irrelevant variables must be controlled in order to create a valid experimental design. Students learning in the 4-variable domain had to equate the values of three different irrelevant variables in each of two experimental designs whereas students learning in the 2-variable domain had to equate the values of only one irrelevant variable in each design. Thus, compared to students in the 2-variable domain, students who learned in the 4-variable domain received more repetition of the point that they needed to equate the values of the irrelevant variables. In addition, they experienced more variation in the combinations of focal and irrelevant variables, which may have helped them to develop a deeper and more generalizable understanding of the rationale for controlling variables. Related to this point, students in the 2-variable condition might have experienced some interference due to the similarity of the two instructional examples they received. Specifically, the two examples were mirror images that required variable X to be manipulated and variable Y to be controlled in the first example, whereas the second example reversed the assignment of the two variables to be manipulated and controlled.

Experiment 2

The teaching intervention designed by Chen and Klahr (1999) has several attributes that are probably important contributors to its effectiveness. First, the logic of the control of variables strategy is developed in a concrete domain (e.g., ramps and balls).

Second, the domain is constrained. There are only four variables and each has only two values. Further, the teacher identifies all the variables, illustrates how to change their values, and establishes the question of interest for any experiment (i.e., the focal variable). Thus, the student is relieved of many of the decisions involved in creating an experiment and can focus on the logic of CVS.

Third, the illustrative experiment intentionally confounds the manipulation of the focal variable with the other three variables in the domain. This is done, in part, to create an opportunity to address a common misconception on the part of students that the goal of an experiment is to produce a desired result (e.g., make the ball go further on one ramp than the other) rather than to isolate the effect of the focal variable.

Fourth, the confounded example also presents an opportunity to emphasize the rationale for controlling irrelevant variables. The teacher accomplishes this by leading the student through a series of observations and questions designed to communicate the importance of equating the values of the three irrelevant variables in order to unambiguously determine whether the focal variable affects how far the ball rolls. Thus, the protocol actively engages the student in the rationale underlying CVS, requiring the student to make observations and answer questions designed to focus on the reason for equating the values of the irrelevant variables.

Fifth, the protocol involves the student in remedying the flaws identified in the confounded design used for illustration. That is, students not only identify the problems with the design, they identify how to correct them. This part of Klahr’s intervention implicitly communicates a procedure for constructing an experimental design. It is this final aspect of the protocol that is the target of our revision of Klahr’s intervention, so we will examine this component more closely.

When correcting the confounded design used to develop the logic of CVS, students are provided with the parameters for one experimental condition (i.e., an already set-up ramp) and they are guided through the process of determining the appropriate parameters of the other experimental condition in order to establish a valid comparison. This is done by directing the students to consider each of the four variables in the domain one at a time. Because of this characteristic of the instruction, we will refer to it as the “variable method” (aka, the “Chen and Klahr method”). For each individual variable, students are prompted to say what the value of the variable should be and are then provided with feedback. If the variable under consideration is not the focal variable, the feedback indicates whether they are correct and states that the variable is not the one being tested so the values should be the same for the two conditions. If the variable under consideration is the focal variable, the feedback indicates whether they are correct and reminds them that the variable is the one being tested so the values should differ for the two conditions. This protocol for guiding students to fix a confounded design communicates a procedure for designing experiments where the variables are considered one-by-one in the same order each time. The protocol may be confusing to students because: (1) it may not adequately establish the critical conceptual distinction between the focal variable and the irrelevant variables and (2) it describes an unnecessarily complex procedure for constructing a valid experiment.

A simpler procedure for instructing students how to design valid comparisons might be the following two-step procedure: (1) start by constructing a comparison where the values of all variables are equated and (2) identify the focal variable and change its value in one of the conditions. Because this procedure begins by equating the values of all variables, we will refer to it as the “equate method.” The Equate Method sharply distinguishes between the focal variable, on the one hand, and the irrelevant variables on the other. In fact, it explicitly recognizes only the focal variable. Thus, the Equate Method should be simpler for a student to represent than the variable-by-variable procedure incorporated into the Variable Method; therefore, it may be a more effective teaching intervention, particularly for students who are struggling with CVS.

Experiment 2 compared the Variable Method and Equate Method with respect to performance on the same ramps and comparison tests used to assess learning of CVS in Experiment 1. If the Equate Method’s description of the procedure for constructing valid experiments is easier for students to understand and remember, it should produce better performance on the ramps test (i.e., a near transfer assessment of learning). On the other hand, the Variable Method has repeatedly been shown to produce robust understanding of CVS, so it may be expected to result in good performance on the ramps test.

The comparison of the two interventions with respect to transfer performance addresses the important issue of the robustness of students’ understanding of the logic of CVS (Koedinger, Booth & Klahr, 2014; Koedinger et al., 2012). If students cannot grasp the logic of CVS as presented in the Variable Method, then the simpler presentation of that logic in the Equate Method may lead to better understanding and thus better transfer performance. On the other hand, although the Equate intervention implies a simpler procedure for designing valid experiments, it does so at the cost of less attention to the logic of controlling the irrelevant variables. Thus, students receiving the Equate intervention may not understand the logic of CVS as well as students receiving the Variable intervention and so may perform worse on the transfer task than students receiving the Variable intervention (Schwartz et al., 2011).

Method

Participants. The participants were 82 fourth-grade students in the Wayne County Public School system in Wooster, OH. The students volunteered from six classrooms in four different schools. Most of the students at each school were white (range 86%-91%). Across the four schools, the proportion of students on free or reduced lunch ranged from 30% to 49%. Across the four schools, the test results on the state-mandated Ohio Achievement Tests for the year during which the study was conducted were: 89%-98% for grade 4 math, 88%-92% for grade 4 reading, 71%-94% for grade 5 science. In short, the students matriculated in schools that performed well in comparison to other schools in the state of Ohio. However, it is difficult to compare this sample of students to the sample in Experiment 1 or those in our previous studies (Lorch et al., 2010; Lorch et al., 2014) because the Ohio Achievement Tests are not directly comparable to the state-mandated tests in Kentucky.

Students were assigned at random to the two intervention conditions with the restriction that an equal number of students participated in each intervention. The final sample consisted of 29 male students and 53 female students. The students and their parent(s)/guardian(s) were all informed of the nature and purpose of the research and consented to participate under the condition that their individual results would be recorded without identifying information.

Materials. The materials consisted of the same ramps apparatus and planning booklet used in Experiment 1. In addition, two of the three comparison tests used in Experiment 1 were used in Experiment 2.

Procedure. In each school, a room was provided for the purposes of conducting the experiment. Students participated individually in the experiment during regular school hours. As in the first experiment, there were four steps to the procedure. First, every student was given a pretest consisting of one of the comparison tests. The assignment of the two tests to serve as pretest or posttest was counterbalanced.

Second, after completing the comparison pretest, the instructor introduced the student to the ramps domain and explained that the student was going to learn how to “make good experiments.” In both intervention conditions, the protocol was identical in all respects to the four-variable condition of the first experiment with the exception of the section explaining how to construct a valid experiment. The Variable Method used exactly the same explanation of how to construct a valid experiment as the four-variable condition of Experiment 1. Specifically, the instructor disassembled one of the ramps and had the student consider the variables one-at-a-time. The student made a decision about how to treat each variable and the experimenter provided appropriate feedback. When the student had produced a valid experimental design, the instructor concluded with an explicit statement of the procedure: “If we want to know whether the length of run affects how far the ball rolls, we have to make the length of run different on ramp A and ramp B, but the ramps must be exactly the same in all other ways – we must use the same steepness, the same type of ball, and the same surface. That way, we’ll be sure that the only difference between the two ramps is their length of run. Then if the ball rolls further on ramp A, we’ll know it must be because of the difference in the length of run.”

For the Equate protocol, the instructor also disassembled one of the ramps and then guided the student to re-design the experiment. However, the instructor directed the student to set up the experiment in two stages: (1) set all four variables of the disassembled ramp to the same values as the four variables on the assembled ramp, (2) then identify the variable being tested and change its value so that the variable differed for the two ramps. When the new, valid comparison was constructed, the instructor concluded with an explicit statement of the procedure: “If we want to know whether the length of run affects how far the ball rolls, we’ll start by making the ramps identical, then we’ll change the length of run for the two ramps. That way, we’ll be sure that the only difference between the two ramps is in their length of run. Then if the balls roll different distances, we’ll know it must be because of the difference in the length of run.”

Both interventions then presented a second confounded example in the ramps domain and repeated the instructional protocols described above. After the second example was completed, both interventions ended with a statement of its procedure for constructing a good experiment.

In the final two steps of the procedure, the student’s understanding of CVS was tested as in Experiment 1. First, the student was given the set of ramps and was asked to conduct four experiments in the Ramps domain testing each of the four variables. The student was provided with a planning booklet for support. After completing the four ramps experiments, the student was asked to complete the second comparison test. The procedure for administering this posttest was identical to the procedure for administering the pretest. The ramps test and comparison test were scored as in Experiment 1.

Results and Discussion

Each student designed experiments to test each of the four possible focal variables in the ramps and balls domain. For each student, the number of correctly designed experiments was recorded. Each student’s performance was also evaluated on the two comparison tests (pretest and posttest). For each test, the proportion of correct answers was computed for each of three item-types: items presenting valid comparisons (valid), items presenting confounded comparisons (confound), and items in which the contrasted variable was not the designated focal variable (noncontrastive). Three of the 82 students (3.66%) scored at least 85% correct on the comparison pretest, demonstrating that they already had a good understanding of CVS. Following Chen and Klahr (1999) and Lorch et al. (2010), the data of these three students were excluded from further data analyses. The results for the ramps test and the comparison tests were analyzed separately. For both sets of analyses, all reported statistical tests are significant beyond the .05 level unless noted otherwise.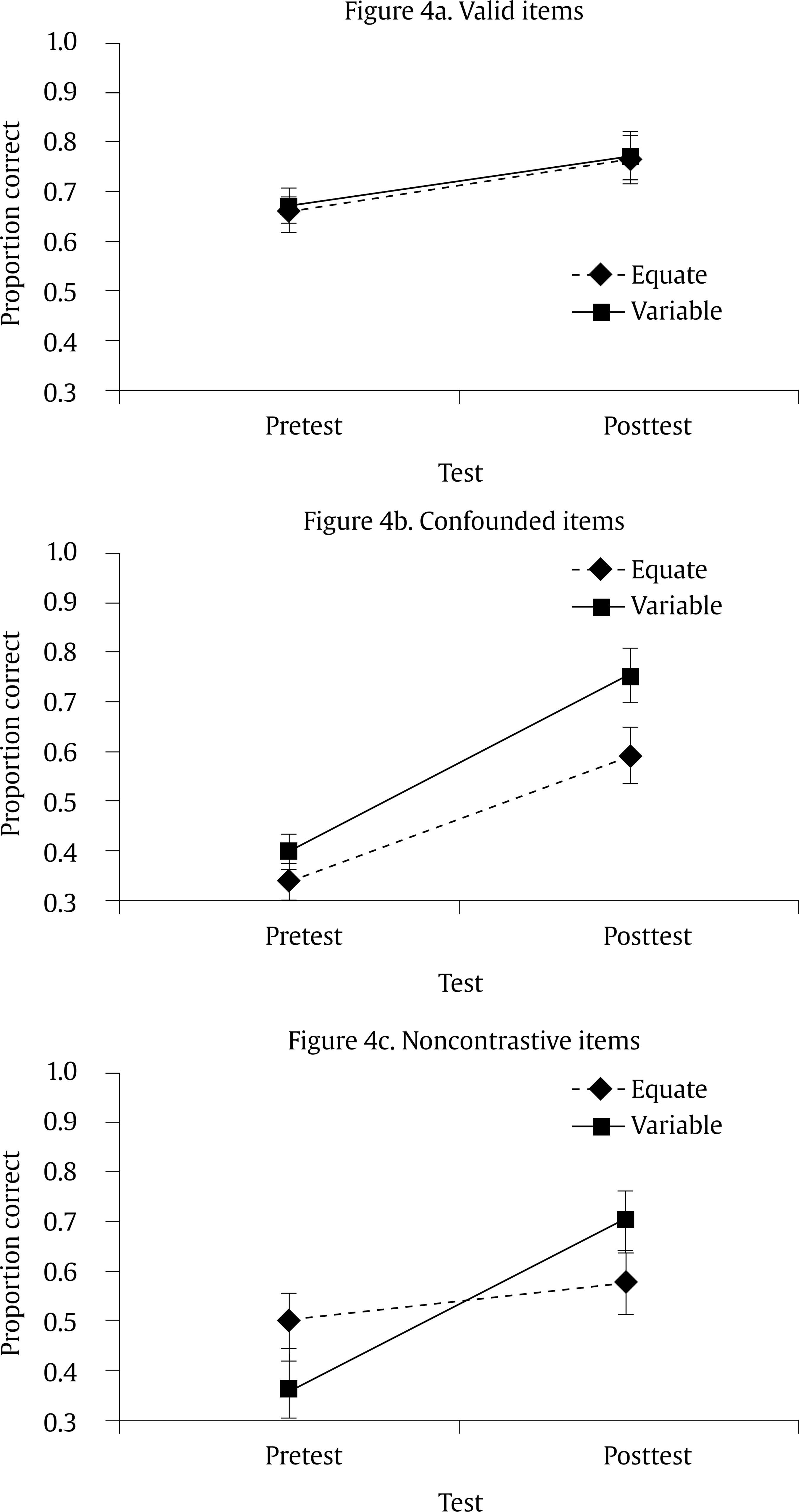

Ramps tests. Recall that we hypothesized that the Equate intervention represents a simpler procedure for designing experiments than the Variable intervention. Thus, we predicted that students would be more successful at designing valid experiments in the Equate condition. However, performance was better in the Variable condition (M = 3.05, SD = 1.36) than in the Equate condition (M = 2.38, SD = 1.71), although the difference did not quite meet conventional significance levels, F(1, 77) = 3.68, partial η² = .046, p = .059. In fact, the levels of performance in both conditions were relatively high. Students designed four experiments, so the mean percentage correct was 76.25% for students receiving the Variable intervention and 59.62% for students receiving the Equate intervention.

Comparison tests. Proportion correct on the comparison tests was analyzed with a mixed-factors ANOVA in which the within-subjects factors were Item-type (valid, confounded, noncontrastive) and Test (pretest, posttest) and the between-subjects factor was Intervention (Variable, Equate). The results are summarized in Figure 4.

There were several results from the overall analysis. There was substantial learning from the pretest (M proportion correct = .49, where chance = .50) to the posttest (M = .69 correct), F(1, 77) = 52.07, partial η² = .40. Further, the amount of learning differed as a function of Item-type, F(2, 154) = 5.75, partial η² = .07. As shown in Figure 4, performance improved much more for the confounded items (M change from pretest to posttest = .30) and noncontrastive items (M change = .21) than for the valid items (M change = .11). More importantly, both effects depended upon the Intervention.

First, the amount of learning depended upon the Intervention, F(1, 77) = 4.23, partial η² = .05. In both conditions, students performed at chance levels on the pretest (.48 in the Variable intervention vs. .50 in the Equate intervention) but improved more after the Variable intervention (M = .74 on posttest) than after the Equate intervention (M = .64 on the posttest).

Second, the improvement from pretest to posttest depended jointly on Item-type and the type of Intervention, F(2, 154) = 2.99, partial η² = .04, p =.053. As can be seen in panel (a) of Figure 1, the two interventions produced approximately equivalent performance on the valid items: F(1, 77) < 1. However, the improvement from pretest to posttest on confounded items was greater for the Variable intervention than for the Equate intervention, F(1, 77) = 4.56, partial η² = .06. There was also more learning associated with noncontrastive items for the Variable intervention than for the Equate intervention, F(1, 77) = 6.67, partial η² = .08.

In sum, when evaluating experimental comparisons in new domains, students taught by the Variable method performed better than students taught by the Equate method. In particular, the better transfer of learning was due to better performance on the two types of invalid comparisons.

General Discussion

Experiment 1 did not produce any support for the hypothesis that limitations in basic cognitive competencies are an important contributor to failures to learn CVS in Chen and Klahr’s (1999) intervention. If many students cannot handle the memory and attentional demands of their intervention, then reducing the number of variables from four to two and providing a template to plan and record the proposed experimental designs should have facilitated learning. In fact, providing a planning booklet had no effect and reducing the number of variables interfered with learning. As argued in the discussion of the results of Experiment 1, the similarity of the instructional examples in the 2-variable condition may have been confusing for students. In addition, the greater variability in the combinations of focal and irrelevant variables in the 4-variable condition may have helped the students to better discern the principle of CVS from the instructional examples. This is generally consistent with findings in the concept-learning literature that variability of exemplars of a concept facilitates learning because it helps learners to distinguish relevant from irrelevant dimensions of variation (Gomez, 2002; Hahn et al., 2005).

Experiment 2 took a different approach to attempting to simplify the learning task for students. Rather than reducing the complexity of the learning environment, we sought to provide a procedure for generating a valid experimental design that was particularly easy to implement. In fact, the simplified procedure resulted in marginally poorer performance on the test of students’ abilities to design valid ramps experiments (i.e., near transfer) and distinctly poorer performance on the test of students’ abilities to evaluate whether comparisons in new domains were valid (i.e., far transfer). Specifically, students in the Variable condition did much better at identifying invalid comparisons than students in the Equate condition. Although the description of the procedure for designing valid comparisons was more complex in the Variable condition than in the Equate condition, the focus on the rationale underlying controlling irrelevant variables resulted in better understanding of CVS.

The superiority of the Variable condition on the noncontrastive items might seem surprising because the Equate condition placed more emphasis on the focal variable. Therefore, students taught by the Equate method might have been expected to be more sensitive to the fact that the wrong variable was manipulated for noncontrastive items. On the other hand, noncontrastive items did follow the correct pattern of one manipulated variable and all other variables equated; this may have been what caused students in the Equate condition to incorrectly endorse noncontrastive items as “good” comparisons.

The development of literacy in scientific methods is a slow and demanding process for students because the domain is complex. A plausible strategy to try to facilitate learning in any complex domain is to introduce students to key concepts in a highly constrained learning environment then introduce more complexity and nuance as the students master basic concepts in the simplified context. However, the results of our study show that there is such a thing as oversimplifying instruction. If key information is lost in simplifying the learning environment, it can be to the detriment of identifying distinctions that are relevant in learning some concept or strategy. Thus, allowing variation in only two variables in Experiment 1 interfered with students’ ability to transfer their understanding of CVS to a new context. In Experiment 2, simplifying the procedure for constructing a valid experimental design was achieved at the cost of less attention to the logic of controlling irrelevant variables and, again, transfer of understanding of CVS suffered.

What are the implications of our findings for professional educators? Based on the findings of this study and those of several related studies investigating variants of Chen and Klahr’s (1999) basic intervention (Klahr & Chen, 2011; Klahr & Nigam, 2004; Lorch et al., 2010; Lorch et al., 2014; Lorch et al., 2017; Strand-Cary & Klahr, 2008; Toth et al., 2000; Triona & Klahr, 2003; Zohar & Aharon-Kravetsky, 2005), the Chen and Klahr intervention is an efficient, robust method of teaching CVS. It is very effective with students who are high-achieving and/or matriculate in higher-achieving schools. It is less effective but currently the most effective intervention yet identified for teaching lower-achieving students and/or students who matriculate in lower-achieving schools. Still, we are left with the question of why the Chen and Klahr teaching intervention is not more effective with lower-achieving students and students from lower-achieving schools (Experiment 1; Lorch et al., 2010; Lorch et al., 2014; Lorch et al., 2017; Zohar & Aharon-Kravetsky, 2005; Zohar & Peled, 2008). These students apparently have the cognitive skills to manage the demands of the teaching protocol yet most of them do not learn the logic of CVS based on a 30-minute lesson. A likely candidate to explain the modest benefits of the intervention with these student populations is a lack of background knowledge – the students simply do not have sufficient familiarity with scientific domains and goals to be ready to tackle the logic of science experiments.

This line of reasoning is compatible with a theoretical position that advocates the potential benefits of learning science in authentic contexts (Dean & Kuhn, 2006; Kuhn, 2005; Kuhn et al., 2015; Schauble, 1996; Schauble, Glaser, Duschl, Schulze, & John, 1991). The Chen and Klahr’s (1999) intervention typically consists of a single, brief session that is focused on a single task domain. In fact, most learning benefits from repeated experiences with a phenomenon across time and with a variety of domains. Repeated exposures across time result in stronger and more flexible representations of a domain (Roediger, Agarwal, McDaniel, & McDermott, 2011). Multiple exposures to the same phenomenon in different contexts also contribute to a mental representation that is flexible and will support generalization to new contexts (Gomez, 2002; Hahn et al., 2005). On this rationale, it is worth exploring whether learning by populations of students who have not shown large benefits from the Chen and Klahr intervention might improve substantially if they receive several lessons at spaced intervals using different domains. This approach would also provide an opportunity to loosen the constraints on the learning environment gradually, thus approaching a more authentic environment by approximations (Duke & Pearson, 2002; Pearson & Gallagher, 1983). For example, variables in a domain might be allowed to have several values, students might be asked to identify variables that could influence performance in the domain, and students might be asked to generate questions to be investigated. As many theorists have emphasized, conducting experiments involves much more than understanding the logic of controlling variables, and developing literacy in scientific methodology requires a great deal of experience with scientific investigations (Kuhn, 2005; Kuhn & Dean, 2005; Schauble, 1996; Zimmerman, 2005). An iterative approach that provides repetition of concepts, variation in the domains considered, and increasing complexity of the situations studied capitalizes on principles that have been well documented to support robust learning (Koedinger et al., 2012; Koedinger et al., 2014).

Although an iterative approach like that described above is implied by researchers who have investigated teaching of CVS in constrained domains (Klahr, Chen, & Toth, 2001; Klahr & Nigram, 2004; Lorch et al., 2010), these researchers have not, for the most part, extended their research programs in this direction. Theorists who have criticized reductionist approaches to teaching science have proposed that young students should be exposed to more authentic learning environments from the start of their education in science (Duschl & Grandy, 2012; Kuhn et al., 2015; Schauble, 1996). These theorists emphasize the many important concepts and skills that are neglected in the constrained learning environments studied in reductionist approaches. They point out that scientists must learn how to ask good questions. They must learn strategies (e.g., experimentation) and skills (e.g., laboratory procedures, statistical procedures) for answering questions. They must evaluate the quality of empirical evidence, cope with apparent contradictions and anomalies in observations, and consider competing models of the same data (Allchin, 2012, 2014; Duschl & Grandy, 2012; Echevarria, 2003; Ford, 2005; German, 1999). They must be able to construct and critique scientific arguments (Dean & Kuhn, 2006; Kuhn, 2005; Kuhn & Dean, 2005) and integrate empirical findings into theoretical explanations that typically involve multiple interacting causes (Kuhn et al., 2015). There is no debate that these are critical components of scientific literacy.

The important debate concerns the best approach to teaching students the many components that must ultimately be integrated to achieve a reasonable level of scientific literacy. Should we start with highly constrained contexts and systematically loosen the constraints to expand and elaborate the concepts of scientific reasoning? Or should we begin with less constrained, more authentic contexts and have students grapple with the many different components of scientific literacy from the start? Surely this is a false dichotomy: the current investigation has shown that a reductionist approach can be taken too far and a simple thought experiment would demonstrate that there are limits to the complexity and hence the “authenticity” a novice in science can handle. Hence, the real question is: what determines the appropriate balance of constraint vs. authenticity in an educational environment that will maximize a given student’s learning? A focus on this question promises to generate a more productive conversation between those who favor a reductionist approach to science teaching and those who emphasize the importance of studying authentic learning environments.