
AnûÀlisis de Redes: una Alternativa a los Enfoques ClûÀsicos de Evaluaciû°n de los Sistemas Educativos
[Network analysis: An alternative to classic approaches for education systems evaluation]
Marcos Álvarez-Díaz1, 4, César Gallego-Acedo1, Rubén Fernández-Alonso1, 4, José Muñiz2 y Eduardo Fonseca-Pedrero3
1Universidade Autû°noma de Lisboa, CIP-UAL/UALG, Lisbon, Portugal; 2Universidade do Minho, Braga, Portugal; 3ISCTE CIS IUL, Lisbon, Portugal; 4Universidade de Lisboa & CIDEFES, Universidade Lusû°fona, Lisboa, Portugal
https://doi.org/10.5093/psed2021a16
Recibido a 23 de Noviembre de 2020, Aceptado a 24 de Marzo de 2021
Resumen
Las abundantes investigaciones sobre los sistemas educativos han permitido identificar los factores fundamentales que determinan el éxito educativo del alumnado. Sin embargo, estas investigaciones no han sido muy eficientes a la hora de transferir los resultados a los contextos aplicados en los que se mueven los profesionales y directivos que toman las decisiones sobre los sistemas educativos. La razón principal de este fracaso proviene de la poca familiarización de los profesionales de la educación con la sofisticada metodología estadística y psicométrica utilizada por la mayoría de los investigadores. El objetivo del presente trabajo es analizar los sistemas educativos mediante la metodología de análisis de redes, la cual es muy asequible, clara e intuitiva para profesionales y directivos educativos sin una gran sofisticación metodológica. Se utilizó una muestra de 7,882 estudiantes de segundo curso de la Enseñanza Secundaria Obligatoria. Se evaluó su competencia matemática y se obtuvieron datos relativos al contexto educativo. Se utilizó para los análisis el análisis de redes, calculando indicadores de centralidad, así como de precisión y estabilidad de la red. Los resultados indican que el autoconcepto y las expectativas académicas tienen un importante efecto sobre los resultados en matemáticas. Los hallazgos convergen con los obtenidos previamente con otros enfoques. El acercamiento de análisis de redes ofrece una combinación idónea entre rigor analítico y sencillez interpretativa, lo que le confiere gran potencial para ser empleado en contextos educativos aplicados para la toma de decisiones basadas en datos.
Abstract
Widespread research on educational systems has made it possible to identify the main factors that define students’ educational success. Nevertheless, these studies have not been very efficient when it comes to transferring their conclusions to the applied contexts where those who teach or make decisions about educational systems move. The main reason for this failure lies on the unfamiliarity of education professionals with the sophisticated statistical and psychometric methodology used by most researchers. The goal of this paper is to analyze educational systems using the Network Analysis methodology, which is very affordable, clear, and intuitive for teachers and educational leaders without a great methodological sophistication. A sample of 7,882 eighth-graders was used. Students’ mathematical skills were evaluated and data were obtained from their educational context. Network Analysis was used calculating indicators of centrality, as well as precision and stability of the network. The results indicate that academic self-concept and academic expectations have an important effect on performance in mathematics. The findings match with those previously obtained with other approaches. The Network Analysis methodology offers an ideal combination of analytical rigor and interpretative simplicity, that provides a great potential to be used in applied educational contexts for evidence-based decision making.
Palabras clave
AnûÀlisis de redes, Rendimiento acadûˋmico, Evaluaciû°n educativa, Sistemas educativosKeywords
Network analysis, Academic performance, Educational assessment, Educational systemsPara citar este artûÙculo: Álvarez-Díaz, M., Gallego-Acedo, C., Fernández-Alonso, R., Muñiz, J. y Fonseca-Pedrero, E. (2022). AnûÀlisis de Redes: una Alternativa a los Enfoques ClûÀsicos de Evaluaciû°n de los Sistemas Educativos. PsicologûÙa Educativa, 28(2), 165 - 173. https://doi.org/10.5093/psed2021a16
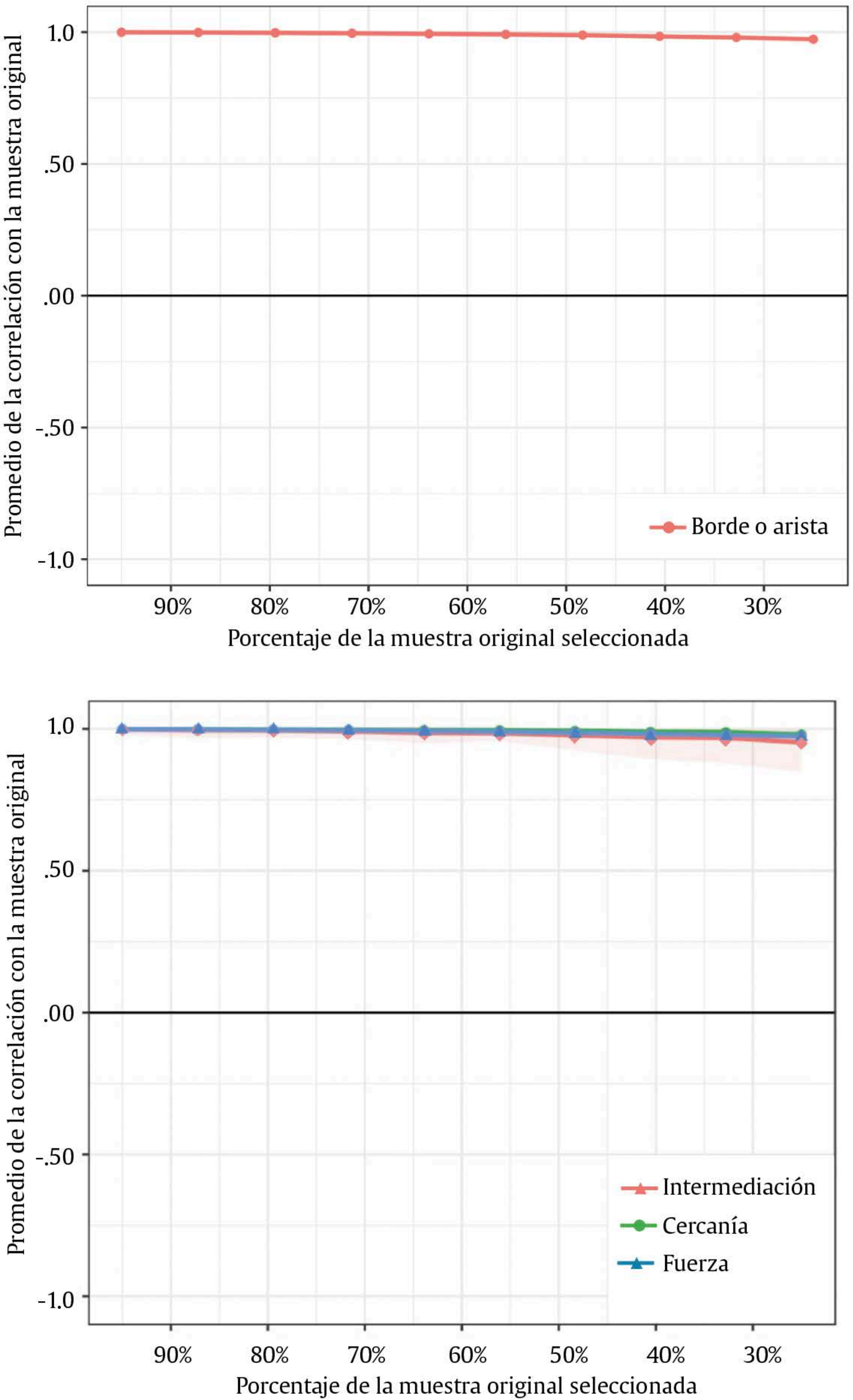
fernandezaruben@uniovi.es Correspondencia: fernandezaruben@uniovi.es (R. FernûÀndez Alonso).La investigación en los factores determinantes del éxito académico de los estudiantes ha seguido dos tradiciones principales: la investigación psicoeducativa y los estudios educativos de ascendencia económico-sociológica (Marchesi y Martín, 1998). Desde la perspectiva psicoeducativa, variables como el autoconcepto, las expectativas de finalización de estudios, las actitudes hacia la lectura y las materias escolares y los estilos de comunicación e implicación familiar son componentes básicos en la determinación del rendimiento académico (Alonso-Tapia y Nieto, 2019; Han, 2019; Huang, 2011; Lane et al., 2004; Petscher, 2010; Suárez-Álvarez et al., 2014). La relación entre autoconcepto académico y resultados educativos parece universal, habiéndose confirmado para todos los rangos edad y circunstancias sociodemográficas, empleando diferentes diseños de investigación, con medidas de autopercepción y rendimiento escolar variadas (Möller et al., 2020). Tal es el volumen de las evidencias, que Stankov et al. (2014) consideran que la percepción de la propia competencia es la variable no cognitiva con mayor impacto en los resultados educativos. Hattie (2009) estimó que la relación entre autoconcepto y resultados educativos era moderada (d = 0.40) y estudios posteriores informan de efectos similares (Stankov, 2013). Möller et al. (2009) en su primer metaanálisis estimaron que la magnitud de r oscilaba entre .43 y .49, y años más tarde la elevaron hasta .56 (Möller et al., 2020). Por su parte, Richardson et al. (2012) obtienen una r = .59 entre ambas variables. Las evaluaciones comparadas de sistemas educativos han confirmado esta relación en más de cien países de muy distintas culturas y tradiciones educativas. Por ejemplo, Trends in International Mathematics and Science Study (TIMSS) informa que la relación entre autoconcepto y resultados en matemáticas es lineal, positiva y estadísticamente significativa, estimando que en el conjunto de países la diferencia en los promedios de matemáticas del alumnado con mayor y menor autoconcepto oscilaba entre 0.79 y 1.05 unidades de desviación típica (UDT; Beaton et al., 1996; Mullis et al., 2005; Mullis et al., 2016). La evaluación a gran escala con muestras españolas apunta en la misma dirección: la diferencia en matemáticas entre los grupos de autoconcepto matemático alto y bajo fue de 0.81 UDT (Beaton et al., 1996), mientras que Suárez-Álvarez et al. (2014) encontraron que la correlación autoconcepto-resultados matemáticos era de r = .46, manteniéndose en un nivel similar (r = .43) después de descontar el efecto de los antecedentes sociodemográficos y otras variables personales como las expectativas o el interés por la materia. Pinquart y Ebeling (2020) identificaron 98 efectos que relacionaban expectativas de finalización de estudios y resultados en matemáticas y estimaron que la fuerza de la relación era moderada (r = .33), si bien la asociación estaba modulada por el nivel socioeconómico, la etnia y la edad del alumnado. Las evaluaciones de sistemas educativos han confirmado estos hallazgos. TIMSS-1999 midió las expectativas de finalización de estudios con un ítem de opción múltiple de cuatro alternativas: estudios obligatorios, secundaria postobligatoria, técnicos de grado superior y universitarios. Para el conjunto de los países la diferencia en matemáticas entre los grupos de expectativas más alta y baja era de 1.27 UDT. Además, salvo rarísimas excepciones, dentro cada país se observó un patrón de resultados similar: relación aproximadamente lineal y positiva y diferencias estadísticamente significativas entre los cuatro grupos comparados (Mullis et al., 2000). Por su parte, en el año 2006 el Programme for International Student Assessment (PISA) preguntó al alumnado si a los 30 años se veía trabajando en alguna profesión que requiriera una titulación en el campo de las ciencias. La respuesta a esta cuestión puede tomarse como un proxy que refleja la esperanza de alcanzar una titulación en las áreas físico-naturales. Para el conjunto de países participantes la diferencia entre el grupo de estudiantes con esta aspiración y los que no la tenían era de 0.44 UDT y en la mayoría de los países la diferencia oscilaba entre 0.33 y 0.55 UDT (OECD, 2007). Las evaluaciones españolas confirman estas evidencias: el Ministerio de Educación (2011), después de evaluar a más de 26,000 estudiantes de 2º de ESO, estimó que la puntuación en las cuatro materias evaluadas del alumnado con expectativas de terminar estudios superiores era entre 0.79 y 1.13 UDT mayor que la del alumnado que solo esperaba terminar estudios obligatorios. Se trata de una diferencia similar a la calculada por Sainz Martínez et al. (2010) con muestras del País Vasco. Finalmente, Suárez-Álvarez et al. (2014) encontraron que la correlación entre expectativas académicas y puntuaciones en pruebas objetivas era de 0.33. No obstante, cuando se controlaba el influjo de los antecedentes sociodemográficos y la historia escolar la fuerza de la asociación descendía (r = .13), aunque seguía siendo estadísticamente significativa. El estudio de la implicación familiar en la educación es un campo de investigación muy productivo (Jeynes, 2018; Kim y Hill, 2015; Patall et al., 2008; Pomerantz et al., 2007; Rodríguez-Rodríguez y Guzmán, 2019; Valle et al., 2019; Wilder, 2014). Las evidencias señalan que en general la implicación familiar familiar es una práctica deseable: la comunicación familiar sobre temas escolares y las expectativas académicas de los progenitores tienen efectos positivos sobre los resultados del aprendizaje (Castro et al. 2015; Fan y Cheng, 2001). No obstante, el constructo implicación tiene varias acepciones y no todas ellas están necesariamente conectadas a mejoras del rendimiento escolar (Boonk et al., 2018; Hill y Tyson 2009; Tan et al., 2019). Los estudios con grandes muestras han confirmado estos efectos ambivalentes de la implicación familiar. PISA, dentro de las opciones para los países, ofrece la posibilidad de aplicar un cuestionario de contexto a las familias. Los resultados señalan que los estudiantes cuyos progenitores tienen un perfil de implicación más controlador tienden a presentar resultados más bajos. Estos hallazgos se confirman en todas las ediciones y materias evaluadas y los efectos apuntan en la misma dirección, independientemente de que los informantes sean las familias o los propios estudiantes (Fernández-Alonso y Muñiz, en prensa). Las evaluaciones de sistema españolas apuntan en la misma dirección: los estudiantes que provienen de hogares donde las familias presentan un perfil más comunicativo obtienen mejores resultados que aquellos cuyos progenitores muestran un comportamiento más controlador sobre las tareas escolares (Fernández-Alonso et al., 2015; Fernández-Alonso et al., 2017). Las actitudes hacia las materias escolares y el gusto por la lectura son otros factores de proceso educativo asociados a los resultados escolares y, por tanto, variables muy estudiadas. Por ejemplo, el índice “gusto por las matemáticas” de TIMSS muestra una relación estable con los resultados matemáticos en todas las ediciones del estudio: en el conjunto internacional la diferencia entre los grupos extremos de actitudes osciló entre 0.43 y 0.61 UDT (Mullis, Martin, Foy y Arora, 2012; Mullis et al., 2008). Además, dentro de los países los hallazgos eran constantes, observándose que ambas variables estaban linealmente asociadas en la práctica totalidad de los países, favoreciendo siempre al alumnado con mejores actitudes hacia la materia. En el caso de España el efecto incluso parece mayor, encontrándose que la diferencia entre los estudiantes con mejores y peores actitudes hacia las matemáticas era 0.75 UTD (Beaton et al., 1996). Por otra parte, Petscher (2010) informa de una relación moderada entre las actitudes hacia la lectura y los resultados escolares (Zr = 0.32), si bien la fuerza de la asociación en educación primaria prácticamente duplica a la calculada para educación secundaria. De nuevo, los estudios de comparación de sistemas educativos confirman estos datos: en las cuatro ediciones del Progress in International Reading Literacy Study (PIRLS) el alumnado con una actitud positiva hacia la lectura presenta mejores resultados que el alumnado con niveles medios y bajos en las actitudes lectoras. La diferencia entre los grupos extremos oscila entre 0.37 y 0.54 UDT (Mullis, Martin, Foy y Drucker, 2012; Mullis et al., 2007). A pesar de que dentro de los países existen importantes variaciones en la fuerza de la asociación, en todos los casos la conclusión es idéntica: las actitudes positivas hacia la lectura y el rendimiento están relacionados significativa y bidireccionalmente, los lectores más competentes tienden a disfrutar más de la lectura y, por tanto, a leer con mayor frecuencia que los lectores más pobres, hecho que les permite desarrollar estrategias de comprensión más avanzadas y de este modo optimizar sus resultados escolares. Los estudios con muestras españolas se encuentran en la misma dirección (Ministerio de Educación, 2011). Por su parte, los estudios educativos de ascendencia sociológica confirman que una parte importante del éxito escolar está determinado por factores antecedentes y de contexto como el capital cultural de la familia y la pertenencia a grupos sociales dominantes (García-Crespo et al., 2019; Palardy et al., 2015; Sirin, 2005; White, 1982). Dentro de los factores de contexto, la variable con mayor fuerza explicativa suele ser un índice, generalmente tipificado, que resume el nivel socioeconómico y cultural de la familia del alumnado o, en su defecto, variables que describen el nivel de estudios y profesiones de los progenitores (Peña-Suárez et al., 2009). También han mostrado efectos diferenciales variables como género, escolarización temprana, lengua materna, condición de emigrante y posesiones materiales y culturales del hogar (Woitschach et al., 2017). En países en vías de desarrollo (por ejemplo, en la evaluación de sistemas educativos latinoamericanos) son significativas variables que generalmente no se consideran en los estudios de países desarrollados: compatibilizar trabajo y estudios, ser indígena e infraestructuras y características de la vivienda familiar (UNESCO-OREALC y LLECE, 2000, 2016). Las evaluaciones a gran escala responden a un diseño de investigación descriptivo ex post facto y, por tanto, el historial académico y específicamente la repetición escolar se considera un factor de entrada o antecedente. La evidencia acumulada sobre esta variable es concluyente, no habiendo dudas de que la repetición tiene importantes efectos negativos sobre el desempeño académico y también sobre los factores socioafectivos del aprendizaje, incluso una vez descontadas las variables de contexto antes mencionadas (Ikeda y García, 2014; Xia y Kirby, 2009). El Análisis de Redes: una Alternativa Metodológica Como se acaba de mostrar, los programas de evaluación de sistemas educativos han fijado las bases del conocimiento de los factores asociados al éxito académico. Sin embargo, la investigación educativa advierte que estas evaluaciones adolecen de problemas de validez consecuencial: en no pocas ocasiones, sus resultados y conclusiones tienen escaso impacto en las políticas educativas y en los planes de mejora de los centros educativos (Taut y Palacios, 2016). Entre las razones de este limitado impacto se ha señalado el hecho de que los modelos de análisis de datos empleados (regresiones clásicas, modelos jerárquico-lineales, ecuaciones estructurales, etc.) son poco comprensibles para los legítimos destinatarios: responsables políticos, direcciones escolares, profesorado y familias (Froemel, 2009; Jornet, 2016). Por ello, uno de los grandes desafíos de las evaluaciones de sistemas educativos es mejorar la información que aportan para que realmente sea clara y comprensible para los receptores, por lo general profesionales no especializados en la tecnología psicométrica y el análisis de datos. En este sentido, el análisis de redes puede ser una alternativa metodológica para paliar, al menos en parte, estos problemas de validez consecuencial. Una red es un grafo, es decir, una representación de un modelo abstracto mediante dos elementos: nodos [nodes], que simbolizan las variables de estudio, y aristas (también denominadas bordes o edges), que representan las conexiones o relaciones entre los nodos. Existen cuatro tipo de grafos según las aristas sean ponderadas o no y dirigidas o no (Epskamp, Maris et al., 2018; Fonseca-Pedrero, 2017, 2018; McNally, 2016; Schmittmann et al., 2013). La red se estima a partir de la matriz de correlaciones simples (red de asociación), parciales (red de concentración) o parciales regularizadas (Epskamp et al., 2017) y el método de estimación depende del tipo de variables empleadas (continuas, categóricas o una combinación de ambas); de la naturaleza de los datos (transversales o longitudinales) y de si estos datos se encuentran anidados o no (Epskamp et al., 2017; McNally, 2016). La red estimada permite también realizar inferencias estadísticas mediante tres clases de medidas: distancia y longitud de la trayectoria más corta, centralidad y conectividad y agrupamiento (Costantini et al., 2015; Golino y Epskamp, 2017; Haslbeck y Fried, 2017; Jones et al., 2018). Finalmente, los modelos de red ofrecen medidas de precisión y estabilidad de los estimadores. Las primeras devuelven el intervalo de confianza de los parámetros de las aristas, mientras que las segundas evalúan la consistencia del grafo mediante procedimientos de remuestreo, que replican la red con menos casos o con menos nodos (Epskamp et al., 2017; Epskamp, Borsboom et al., 2018). En definitiva, el análisis de redes ofrece una combinación adecuada de rigor analítico y sencillez interpretativa para que los destinatarios de los estudios de factores asociados al rendimiento puedan utilizar la información obtenida en la toma de decisiones y el diseño de planes y programas de mejora. Además, el modelo de red entiende la realidad como un sistema complejo y dinámico (Cramer et al., 2016), lo cual epistemológicamente es perfectamente aplicable al terreno educativo, donde la aproximación sistémica es el marco teórico dominante en la evaluación de sistemas educativos (Adams y Wu, 2002; Mullis et al., 2002; Scheerens, 2016; Towsend, 2007). El análisis de redes no es nuevo en la investigación científica, aplicándose en áreas como las redes sociales bajo la teoría de grafos (Borgatti et al., 2009; Newman, 2010), la psicología (Borsboom, 2017; Borsboom y Cramer, 2013; Schmittmann et al., 2013) y la educación (Govorova et al., 2020). No obstante, hasta donde alcanza nuestro conocimiento, el modelo de red nunca ha sido aplicado al estudio de los factores asociados al rendimiento académico en la evaluación de sistemas educativos. En este contexto, la finalidad del presente trabajo es valorar las posibilidades del análisis de redes para reproducir y modular la relación estructural que se establece entre los factores asociados al éxito escolar en el marco de la evaluación de sistemas educativos. Los objetivos específicos se concretan del siguiente modo: a) estimar la red y analizar la topografía de asociaciones que se establecen entre el rendimiento matemático y las variables sociodemográficas, escolares y personales del alumnado asociadas a dicho rendimiento, b) analizar e interpretar los índices de centralidad de las variables y c) estudiar la precisión y estabilidad de los estimadores de la red. Participantes La muestra estuvo compuesta por 7,882 estudiantes de 2º de ESO del Principado de Asturias. En realidad, se trata de la población, ya que el estudio se realizó sobre el censo del alumnado matriculado en el curso mencionado. La media de edad fue 14.1 años (DT = 0.65). El 47.4 % eran mujeres, el 9.7 % extranjeros y el 26.2 % se encontraba un curso por debajo del correspondiente a su edad. Instrumentos de Medida Prueba de matemáticas. El rendimiento matemático fue evaluado mediante una prueba objetiva, cuyas especificaciones de contenido pueden consultarse en Consejería de Educación, Cultura y Deporte del Principado de Asturias (2012). Se construyó un banco de ítems según el protocolo establecido en Fernández-Alonso (2004). Se seleccionaron 36 ítems de tres formatos: elección múltiple, abiertos de respuesta corta y de respuesta construida, que fueron distribuidos a diferentes modelos de cuadernillos siguiendo un diseño matricial (Fernández-Alonso y Muñiz, 2011). Cada estudiante respondió a un cuadernillo de 24 ítems en una sesión de 50 minutos. En función de su formato, los ítems se calibraron y ajustaron al modelo logístico de 1 parámetro y al modelo de crédito parcial, empleando el programa ConQuest 2.0 (Wu et al., 2007). Para la calibración inicial de los ítems se seleccionaron 2,000 estudiantes de la muestra inicial, lo que aseguraba que cada ítem se respondiera por 500 estudiantes. Una vez comprobado el ajuste, se estimaron los parámetros de los ítems. Estos valores paramétricos, junto con algunas características sociodemográficas y personales del alumnado y de los centros, fueron usados como valores iniciales para calcular la puntuación del alumnado (Fernández-Alonso y Muñiz, 2019). Finalmente las puntuaciones fueron transformadas a una escala normal de media 500 puntos y desviación típica 100, N(500, 100). Variables sociodemográficas. Los antecedentes sociodemográficos del alumnado se describieron mediante tres variables: género (1 = ser mujer), nacionalidad (1 = ser emigrante) y el índice socioeconómico y cultural de las familias (ISEC). El ISEC resume el nivel de estudios y el prestigio profesional de las profesiones de los progenitores y fue construido mediante un análisis de componentes principales y expresado en una escala N(0, 1), siguiendo procedimiento descrito en Peña-Suárez et al. (2009). Para asegurar la calidad del dato la información sobre estudios y profesiones familiares fue facilitada por los tutores del alumnado. Historial académico del alumnado: haber repetido curso. El registro administrativo de matriculación permite identificar al alumnado escolarizado uno o dos cursos por debajo del correspondiente a su edad. En la gran mayoría de estos casos el retraso está motivado por estar repitiendo o haber repetido antes de 2º de ESO. Se codificó una variable dicotómica donde 1 identifica al alumnado repetidor. Cuestionario de contexto del alumnado. A partir de las respuestas del alumnado a un cuestionario se generaron cinco variables. Cuatro de ellas eran continuas y se construyeron por computación y la restante mediante recodificación. Las variables expresadas en escala continua fueron creadas del siguiente modo: el cuestionario contenía una serie de afirmaciones que debían valorarse en una escala Likert de 4 niveles (siendo 0 = muy en desacuerdo y 3 = muy de acuerdo). La puntuación se calculó como la media de las valoraciones del alumnado a los ítems correspondientes, si bien previamente se realizó un análisis de componentes principales para explorar la unidimensionalidad de cada variable. Por tanto, mayores puntuaciones señalan mayor grado de acuerdo con las afirmaciones. A continuación se enumeran los ítems de las cuatro variables y finalmente se describe el proceso de recodificación empleado en la quinta variable: - Autoconcepto académico. Se construyó con las respuestas a cinco ítems: “aprendo fácil”, “soy buen estudiante”, “saco buenas notas”, “mis profesores creen que soy buen estudiante” y “mi familia me considera buen estudiante”. - Índice de lectura. Se construyó con las valoraciones realizadas a tres afirmaciones: “me gusta leer”, “comprendo lo que leo” y “uso la biblioteca del centro”. - Apoyo familiar al estudio. Se construyó sobre dos ítems: “en mi casa hablamos del trabajo escolar” y “mi familia prima el trabajo escolar sobre el ocio”. - Actitud hacia las matemáticas, construida con las respuestas a dos ítems: “Matemáticas es mi asignatura preferida” y “me gustan los ejercicios de Matemáticas”. - Expectativas académicas. El cuestionario contenía esta pregunta: “¿Qué nivel de estudios esperas terminar?” y ofrecía las siguientes opciones de respuesta: (a) estudios obligatorios, (b) FP de grado medio, (c) Bachillerato, (d) estudios superiores y (e) aún no lo sé. Las alternativas se recodificaron como el número de años de escolarización equivalentes a la expectativa académica declarada: estudios obligatorios = 10, secundaria postobligatoria (Bachillerato o FP de grado medio) = 12 y estudios superiores = 15. Parece confirmado que los estudiantes con indecisión vocacional presentan mejores resultados que aquellos que sólo esperan terminar estudios obligatorios (Suárez-Álvarez et al., 2014), por lo que la alternativa “aún no lo sé” fue codificada a 11 puntos. Procedimiento La prueba se desarrolló dentro del programa de evaluación externa de la administración educativa mencionada. Dentro de cada centro las direcciones escolares se encargaron de organizar la prueba y la aplicación se realizó de acuerdo con las instrucciones para el desarrollo de la evaluación de diagnóstico establecidas por la Consejería de Educación del gobierno autonómico. La aplicación corrió a cargo del profesorado que no impartía docencia al alumnado participante, donde cada estudiante respondió a la prueba cognitiva y al cuestionario reseñado. El control de calidad de la aplicación corrió a cargo del Servicio de Inspección Educativa. Análisis de Datos La red de rendimiento matemático, ponderada y no dirigida, fue estimada para la muestra total del alumnado mediante el algoritmo Fruchterman-Reingold. Se trata de una red de concentración, ya que en la estimación se empleó la matriz de correlaciones parciales. Dado que la red contiene variables continuas y dicotómicas en su estimación se utilizó el método modelo Mixed Graphical (MGM; Haslbeck, 2019). Para realizar inferencias a partir de la red se calcularon las medidas de centralidad de los nodos. Las medidas de centralidad utilizadas fueron fuerza, intermediación y cercanía. La fuerza es una medida de centralidad que permite inferir la importancia relativa del nodo en la red estimada. Se refiere a la magnitud de la asociación con los demás nodos, esto es, qué nodo tiene las conexiones más fuertes. Un nodo con una centralidad alta en este parámetro es un nodo que influye en muchos otros nodos. Para evaluar el grado de precisión de la red se estimaron los intervalos de confianza de las aristas. Finalmente para comprobar la estabilidad de la red se calcularon los índices de fuerza de centralidad de los nodos empleando el método de remuestreo bootstrap (Epskamp et al., 2017). El rango de valores perdidos en las variables osciló entre el 0% y el 12.7%. Para recuperar los datos perdidos se siguió el procedimiento establecido por Fernández-Alonso et al. (2012). En los análisis se emplearon los programas estadísticos SPSS v22 (IBM Corp Released, 2013), R (R Core Team, 2016), Qgraph (Epskamp et al., 2012) y JASP (https://jasp-stats.org/). Red Estimada de Rendimiento Académico La red estimada se presenta en la Figura 1 y los valores de centralidad en la Figura 2. En primer lugar, se aprecia un grafo compacto con las variables interconectadas entre sí. Por la magnitud de sus índices de centralidad la variable nuclear del modelo es el resultado en matemáticas (Figura 2). Figura 1 Red estimada de rendimiento académico en matemáticas.  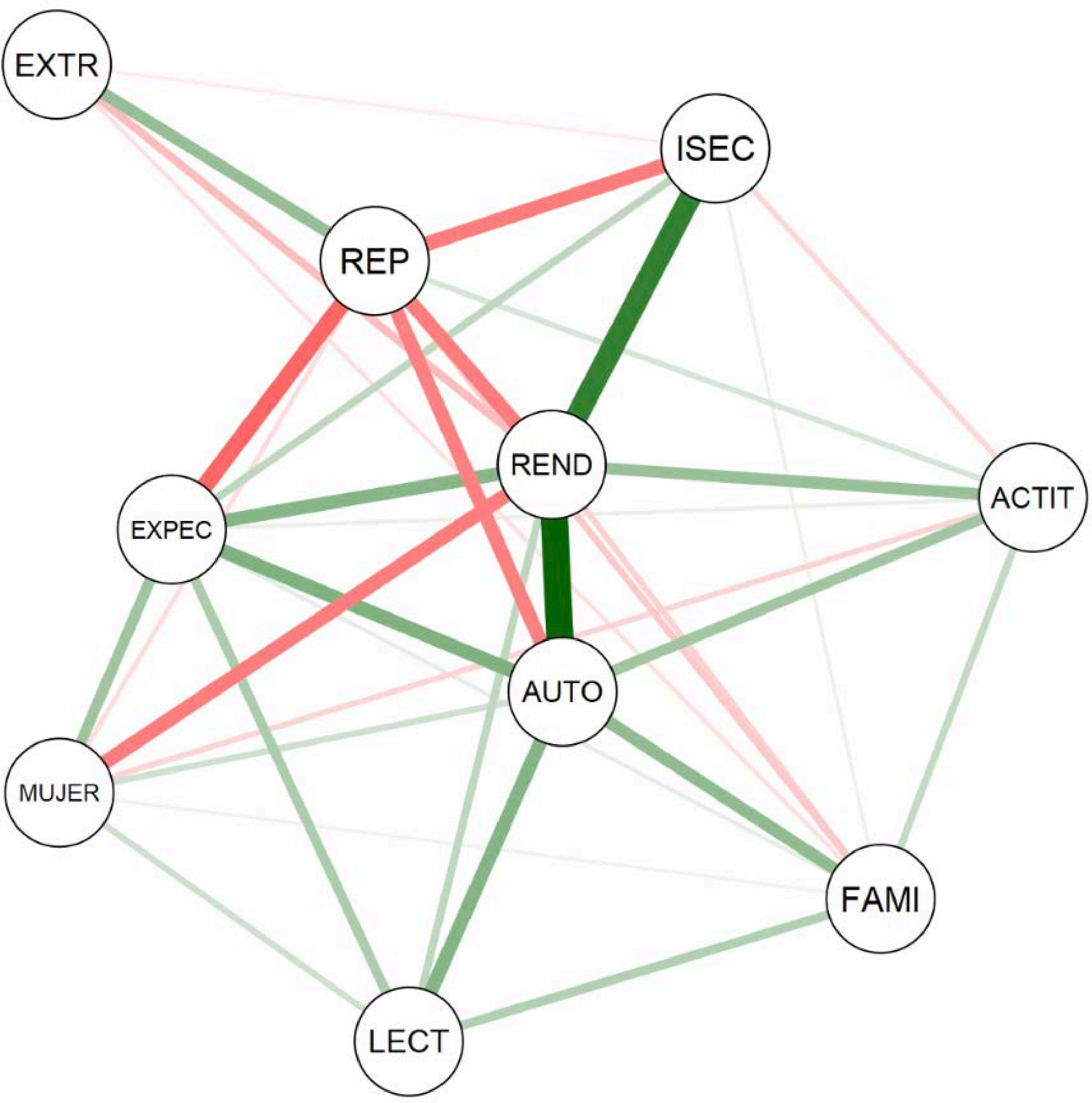 Nota. REND = rendimiento en matemáticas; mujer = ser mujer; EXTR = ser extranjero; ISEC = índice socio-económico y cultural; REP = haber repetido; ACTIT = actitud hacia las matemáticas; AUTO = autoconcepto académico; EXPEC = expectativas académicas; LECT = gusto por la lectura; FAMI = apoyo familiar. Los círculos representan nodos o variables y las líneas representan las aristas o bordes que relacionan los nodos. A mayor valor absoluto del coeficiente de correlación, mayor grosor de la arista y, por tanto, asociación más fuerte entre nodos. Las aristas de color verde indican relaciones positivas entre dos variables, mientras que las de color rojo señalan asociaciones negativas entre las variables. Figura 2 Índices de centralidad para la red estimada de rendimiento académico en matemáticas.  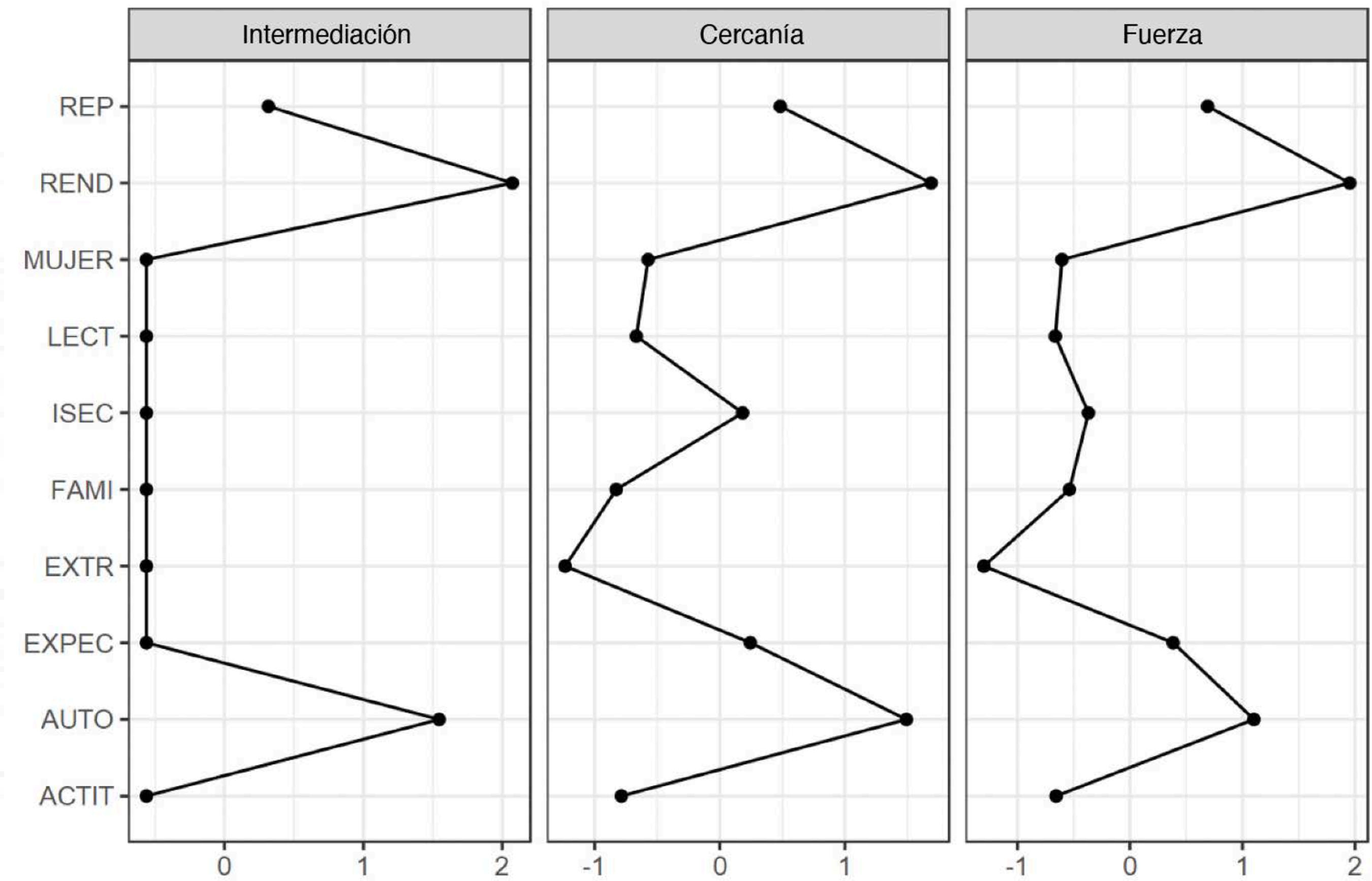 Nota. REND = rendimiento en matemáticas; mujer = ser mujer; EXTR = ser extranjero; ISEC = índice socio-económico y cultural; REP = haber repetido; ACTIT = actitud hacia las matemáticas; AUTO = autoconcepto académico; EXPEC = expectativas académicas; LECT = gusto por la lectura; FAMI = apoyo familiar. La variable ligada más estrechamente al desempeño matemático es el autoconcepto académico, el cual presenta también uno de los índices de fuerza de centralidad más altos en el conjunto de las variables estudiadas. El resto de las variables psicológicas y actitudinales (expectativas de estudio, actitud hacia las matemáticas y gusto por la lectura) están conectadas positivamente entre ellas y también con la puntuación en matemáticas ofreciendo una solución muy coherente. La historia escolar de repetición es otra variable importante en el modelo. Se encuentra negativamente relacionada, tanto con el resultado en matemáticas como con otros predictores importantes del rendimiento académico: ISEC, expectativas y autoconcepto académico. Por el contrario, muestra una asociación positiva con la condición de extranjero. Todo ello parece mostrar que la repetición afecta en mayor medida al alumnado de contextos desfavorecidos y tiene un impacto negativo en la percepción de la propia competencia y en las aspiraciones futuras. Entre los antecedentes de contexto destaca el ISEC, que muestra una asociación positiva con los resultados en matemáticas y con las expectativas académicas. Otra variable sociodemográfica que merece atención es el género del alumnado. La condición de mujer aparece asociada positivamente con el gusto por la lectura, las expectativas y el autoconcepto académico y negativamente con la repetición. Sin embargo, el grafo muestra que las mujeres tienden a presentar puntuaciones más bajas en la prueba de matemáticas y en la actitud hacia la materia. Precisión de la Red Estimada y Estabilidad de la Centralidad La precisión de los estimadores de los pesos de las aristas (bordes) y su intervalo confidencial (IC) al 95% se recoge en la Figura 3. La línea roja muestra el valor del borde estimado en la muestra, mientras que el contorno gris que la rodea indica el IC de los estimadores al 95%. La robustez de los pesos de los bordes se puede examinar analizando los intervalos de confianza: a menor IC mayor robustez. En general los IC son pequeños señalando que los estimadores tienen una precisión satisfactoria. El eje Y recoge todos los pares de variables comparados ordenados descendentemente por la magnitud de los bordes o aristas que las conectan. El par de nodos mejor conectado es la puntuación en matemáticas y el autoconcepto académico, si bien existen un buen número de pares con efectos positivos y significativos. En el extremo contrario se observa que las aristas que conectan repetición con diferentes variables presentan efectos negativos y significativos. En los casos donde el intervalo contiene el valor 0 la relación entre pares de nodos no es significativa desde el punto de vista estadístico. A la vista de estos resultados, se puede afirmar que la red estimada mostró una adecuada precisión en la estimación de los bordes. El análisis de la estabilidad de la fuerza de centralidad se muestra en la Figura 4. La misma recoge el deterioro del indicador de centralidad a medida que se detrae de forma progresiva un porcentaje de la muestra de participantes (90%, 80%, etc.). La línea indica la correlación entre las estimaciones de los índices de centralidad de la muestra completa y las estimaciones de dichos índices cuando se utiliza una submuestra reducida en cada ocasión (al 90%, 80%, etc. hasta llegar a una disminución del 25% de la muestra original). Cuando la correlación desciende por debajo de .70, las estimaciones se vuelven inestables, recomendándose que no descienda de .70 con la mitad de la muestra. Como se puede observar en la Figura 4, la estabilidad de las estimaciones de fuerza no disminuyó y se mantuvo por encima del .90 incluso después de reducir la muestra más del 50%. Estos resultados indican que la red estimada parece muy estable. Figura 3 Estabilidad de los bordes o aristas.  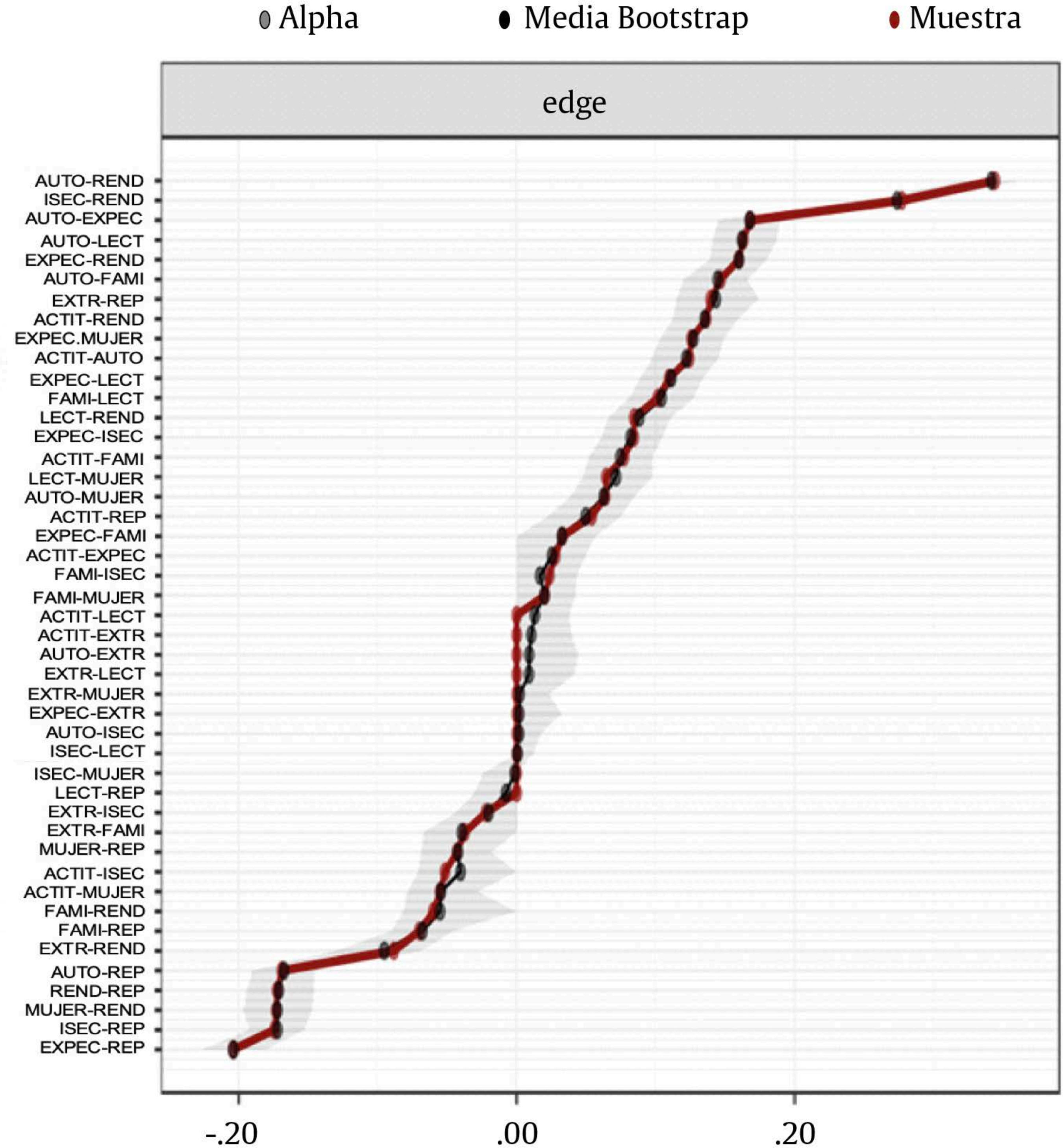 Nota. REND = rendimiento en matemáticas; mujer = ser mujer; EXTR = ser extranjero; ISEC = índice socio-económico y cultural; REP = haber repetido; ACTIT = actitud hacia las matemáticas; AUTO = autoconcepto académico; EXPEC = expectativas académicas; LECT = gusto por la lectura; FAMI = apoyo familiar. Este trabajo tenía por objetivo realizar un estudio de factores asociados al rendimiento académico empleando una nueva aproximación metodológica: el análisis de redes. Hasta donde alcanza nuestro conocimiento es la primera vez que el análisis de redes se emplea para estudiar los factores de calidad en la evaluación de sistemas educativos y, como se expondrá a continuación, los resultados parecen prometedores. El primer lugar cabe destacar que el resultado en matemáticas está positivamente relacionado con el conjunto de variables psicológicas (autoconcepto, expectativas de finalización de estudios y actitudes hacia la materia), tal y como se preveía a la luz de la investigación precedente (Huang, 2011; Petscher, 2010). De hecho, el autoconcepto académico tiene los índices de centralidad más altos y la conexión más estable y robusta con el rendimiento matemático. Todo ello es coherente con la evidencia previa que señala que el autoconcepto es la variable no cognitiva que mejor predice los resultados educativos (Möller et al., 2009; Möller et al., 2020; Richardson et al., 2012; Stankov, 2013; Stankov et al., 2014). También es destacable que una segunda variable de carácter psicoeducativo, la expectativa de finalización de estudios, presenta índices de centralidad más altos que el predictor por antonomasia en términos sociológicos, el nivel socioeconómico y cultural, lo que es compatible con las conclusiones de Suárez-Álvarez et al. (2014) cuando afirman que el potencial de ganancia en los resultados escolares de las variables orécticas es mayor que el esperado por los factores antecedentes y de contexto. Por su parte, la repetición escolar, no sólo se asocia a puntuaciones más bajas en el test. Los hallazgos también señalan que está vinculada con la clase social y la pertenencia a grupos minoritarios (p. ej., condición de emigrante) y asociada a deterioros en factores clave para el éxito escolar como el autoconcepto y las expectativas de estudio, lo que es compatible con el corpus de investigación disponible (Ikeda y García, 2014; OECD, 2013). Las variables antecedentes funcionan en la línea esperada: el ISEC y la condición de emigrante correlacionan negativamente con los resultados en la línea de lo apuntado por Palardy et al. (2015) y Sirin (2005). Finalmente, las mujeres presentan resultados más bajos en matemáticas, hecho que se confirma en la mayoría los países de la OCDE, incluido España (OECD, 2014). En definitiva, los resultados obtenidos empleando el análisis de red confirman las evidencias previas sobre los determinantes del éxito escolar. Era algo esperado, ya que el análisis de redes toma como base la matriz de correlaciones parciales y por tanto sus conclusiones son congruentes con las aportadas por los modelos matemáticos habitualmente empleados (regresiones clásicas, modelos multinivel, etc.), que parten del estudio de las matrices de correlaciones o covarianzas. En ese sentido, como ocurre en otros casos modelos psicométricos (p. ej., TCT vs. TRI) (Muñiz, 2018), el análisis de redes no debe ser visto como alternativa analítica excluyente sino complementaria a los modelos psicométricos ya existentes (Fonseca-Pedrero, 2018). Sin embargo, el análisis de redes tiene dos ventajas prácticas. La primera es evidente: presenta los resultados de un modo gráfico e intuitivo. Este hecho en absoluto es trivial, ya que ofrece amplias posibilidades para comunicar y divulgar los resultados de las evaluaciones con grandes muestras a audiencias habitualmente interesadas, pero que no acceden a los mismos o no los explotan en su plenitud al no estar especializadas en el análisis de datos. La información del análisis de redes puede ser fácilmente entendible por responsables políticos, directivos, docentes y otros usuarios del servicio educativo. Por ello consideramos que el análisis de redes supone una oportunidad para mejorar la devolución de la información en las evaluaciones educativas de alto impacto y, por tanto, puede contribuir a mejorar la validez consecuencial de los programas de evaluación externa. Además, los postulados epistemológicos del modelo de red son perfectamente compatibles y aplicables al estudio de la realidad educativa. En ese sentido la red representa o reproduce mucho mejor que los modelos aditivos de regresión la complejidad de las relaciones entre las variables personales, escolares y sociodemográficas. Por ello, el modelo de red es un enfoque prometedor en la forma de observar, medir, analizar, conceptualizar, comprender, comunicar e intervenir en los fenómenos educativos a múltiples niveles (alumnado, profesorado, centro o sistema educativo). No debería descartarse el hecho de que esta forma de presentar los datos proporcione ideas valiosas sobre las conexiones del aprendizaje o el rendimiento académico en una amplia diversidad de contextos y en niveles de análisis. Con todo, no se debe perder de vista que el análisis de redes es un campo en expansión que se encuentra en sus estadios iniciales, por lo que no está exento de limitaciones (Guloksuz et al., 2017). Por ejemplo, los modelos de redes aún no están consolidados y son computacionalmente complicados, incluso para los expertos en la materia. Es cierto que en este breve periodo de tiempo ya se han realizado excelentes aportaciones científicas, reflejo del interés que ha suscitado entre los profesionales e investigadores (Fried y Cramer, 2017). Sin embargo, en el campo de la educación los estudios son casi inexistentes y por tanto las limitaciones aún más acusadas. Como en otras cuestiones el desafío científico está en cómo conectar adecuadamente la teoría con los datos. En ese sentido, el desarrollo de un modelo teórico-formal (network theories) aplicado al campo de la psicología educativa es una tarea pendiente. Precisamente por su bisoñez en el terreno de la investigación educativa el análisis de redes supone también una oportunidad, atisbándose muchas líneas de trabajo interesantes que se abrirán paso en los próximos años. Primero, muchos fenómenos escolares son de naturaleza jerárquica (Woitschach et al., 2019) y por tanto será necesario desplazarse hacia modelos de redes multinivel que permitan integrar información proveniente de niveles jerárquicamente anidados. Segundo, los procesos de escolarización son dinámicos (longitudinales), por lo que será necesario analizar las redes y sus relaciones estructurales a lo largo del tiempo. Desde la perspectiva de las evaluaciones externas cabría la posibilidad de estudiar la evolución de la red a nivel de centro a lo largo del tiempo o en función de la incorporación de diferentes políticas educativas. Tercero, sería interesante desarrollar programas de análisis más sencillos que pudieran ser aplicados por los profesionales de la educación, sin necesidad de ser experto en análisis de datos. Cuarto, como ocurre con otras técnicas, el análisis de redes también se podría combinar con información proveniente tanto del nivel cuantitativo como cualitativo. In recent decades, educational research and, specifically, evaluations of educational systems have identified a set of factors associated with academic success. The study of these factors is based on two great traditions: psychoeducational research and studies of sociological descent. From the psychoeducational perspective, it has been pointed out that variables such as academic record, self-concept, expectations of completion of studies, attitudes towards reading and school subjects, communication styles, and family involvement are basic components in the academic performance equation (Alonso-Tapia & Nieto, 2019; Han, 2019; Huang, 2011; Ikeda & García, 2014; Lane et al., 2004; Petscher, 2010; Suárez-Álvarez et al., 2014). At the same time the sociological research warns that an important part of school success is determined by the family’s socioeconomic and cultural level and other sociodemographic variables such as gender or belonging to dominant social groups (Palardy et al., 2015; Sirin, 2005). Despite the fact that the evidence from the analysis of factors associated with performance is well established, researchers point out that these studies suffer from problems of consequential validity: many times their results have a limited impact on educational policies and on the improvement plans of the schools (Taut & Palacios, 2016). Among the reasons for this limited impact is the fact that the utilised data analysis models are not understandable to its legitimate recipients: policy makers, school leaders, teachers, and families (Froemel, 2009; Jornet, 2016). Therefore, one of the challenges of educational system evaluations is to improve the information they provide so that it is clear and understandable for recipients, usually professionals not specialized in psychometric technology and data analysis. Network Analysis is a methodological alternative that can mitigate the problems of consequential validity. The network model understands reality as a complex and dynamic system (Cramer et al., 2016), so it is epistemologically applicable to the study of associated factors, since the systemic approach is the dominant theoretical framework in research on factors associated with academic performance (Adams & Wu, 2002; Scheerens, 2016). In addition, network analysis offers an appropriate combination of analytical rigor and interpretive simplicity so that the recipients of these studies can use the information in decision-making and the design of improvement plans and programs. However, as far as our knowledge reaches, the application of the network model to the study of factors associated with academic performance has not been used so far. In this context, the present work sets two specific objectives: - Adjust a network model that represents graphically the relationships between mathematical performance and students’ sociodemographic, school, and personal variables associated with that performance. - Analyze indicators of strength, centrality, stability, and reproductivity of the proposed model to assess the possibility of generalizing this methodological approach to the study of factors related to school performance. Method Participants. The sample consisted of 7,882 Spanish 8th graders of 14.1 years of age (SD = 0.65); 47.4% were women, 9.7% were foreigners, and 26.2% were in a grade below the one corresponding to their age. Instruments Cognitive math test: 36 items in different booklet models following a matrix design (Fernández-Alonso & Muñiz, 2011). Each student completed a booklet of 24 items in a 50-minute session. Variables of sociodemographic adjustment: gender, nationality and Socioeconomic and Cultural Index of families (SECI). Student academic history: grade retention. Some students were identified one or two grades below that corresponding to their age. Student context questionnaire: Academic self-concept, reading index, family support, attitude towards mathematics, and academic expectations. Process. The external evaluation test was conducted by the Scholl masters and the inspection service performed the quality control. Data analysis. The network was estimated for the total student sample using the Fruchterman-Reingold algorithm. It is a concentration network given that the partial correlation matrix was used. Since the network contains continuous and dichotomous variables, the mixed graphical model (Haslbeck, 2019) was used. The centrality measures of the nodes were calculated to make inferences, and the confidence intervals of the edges were estimated to assess the degree of accuracy of the network. Finally, to verify the stability of the network, centrality strength measures of nodes were calculated using the bootstrap resampling method (Epskamp et al., 2017). Results The core variable is the performance in mathematics because of its central position in the network and the magnitude of its centrality measures. Academic self-concept is the most closely linked variable to performance and the one with the highest centrality rates. The rest of the psychological and attitudinal variables are positively connected with each other and with the performance in mathematics which offers a coherent solution. The school history of grade retention is negatively related. In the context variables, SECI stands out and has a positive and significant correlation with results and with academic expectations. It is further noted that women appear to show a positive association when it comes to being fond of reading, when dealing with expectations and academic self-concept, but negatively with regards to grade retention. However, lower scores are presented in the math test and in the attitude towards the subject. The precision of the weights of the edges and their confidence interval (CI) at 95% indicate that they are small and therefore the estimators have a satisfactory precision. The best connected pair of nodes is performance in mathematics and academic self-concept. On the opposite extreme, the edges that connect grade retention with different variables have negative and significant effects. The stability of the centrality force is observed in the fall of the centrality indicator as a percentage of the sample is deducted. Stability did not decrease and remained above .90 even after reducing the sample more than 50%. These results indicate the estimated network stability. Discussion The results showed by the network are compatible with previous evidence on the determinants of school success. Academic self-concept and academic expectations are the psychoeducational variables with the most influential effect on mathematical performance (Pinquart & Ebeling, 2020; Stankov, 2013). Grade retention and socioeconomic and cultural level of the family stand out among background and context factors (Ikeda & García, 2014; Palardy et al., 2015). Network analysis, in addition to replicating the results, presents the results graphically and intuitively and can be easily understood by policy makers, principals, teachers, and any other users of the educational service. In addition, the network reproduces the complexity of relationships between personal, school, and socio-demographic variables better than additive regression models. While it is true that network analysis has limitations (Guloksuz et al., 2017), it is also an opportunity. First, many school phenomena are of a hierarchical nature (Woitschach et al., 2019) and, therefore, multilevel network models will be necessary. Second, processes are dynamic (longitudinal) and, therefore, it will be necessary to analyze networks over time. From external evaluations it would be possible to study the evolution of the network at school level over time or depending on the implementation of new educational policies. Conflict of Interest Los autores de este artículo declaran que no tienen ningún conflicto de intereses. Agradecimiento Este trabajo ha sido posible gracias al apoyo recibido por parte de la Consejería de Educación del Gobierno del Principado de Asturias. Cite this article as: Álvarez-Díaz, M., Gallego, C., Fernández-Alonso, R., Muñiz Fernández, J. y Fonseca-Pedrero, E. (2021). Análisis de redes: una alternativa a los enfoques clásicos de evaluación de los sistemas educativos. Psicología Educativa, 28(2), 165-173. https://doi.org/10.5093/psed2021a16 Financiación. Esta investigación ha sido financiada con fondos FEDER en el PO FEDER de La Rioja 2014-2020 (SRS 6FRSABC026) y el MINECO (referencia PSI2017-85724-P). Referencias |
Para citar este artûÙculo: Álvarez-Díaz, M., Gallego-Acedo, C., Fernández-Alonso, R., Muñiz, J. y Fonseca-Pedrero, E. (2022). AnûÀlisis de Redes: una Alternativa a los Enfoques ClûÀsicos de Evaluaciû°n de los Sistemas Educativos. PsicologûÙa Educativa, 28(2), 165 - 173. https://doi.org/10.5093/psed2021a16
fernandezaruben@uniovi.es Correspondencia: fernandezaruben@uniovi.es (R. FernûÀndez Alonso).Copyright © 2026. Colegio Oficial de la Psicología de Madrid








 e-PUB
e-PUB CrossRef
CrossRef JATS
JATS








