Contribution of Attentional Networks to Basic Arithmetic Achievement in School-age Children

Introduction

During the last decades, multiple studies have been conducted to identify the origin of difficulties in mathematics. In this regard, two fundamental hypotheses have been put forward. The first hypothesis proposes that the development of mathematical competence (and consequently of arithmetic) relies on the development of domain-specific foundational skills (basic numerical skills) (Butterworth, 2005; Dehaene, 1997), including basic numerical skills (e.g., subitizing, estimating, counting, and comparing sets), knowledge of numerical symbols (e.g., knowing and identifying the name of numbers both in Arabic format and numerals), and the ability to understand that numerical symbols represent a non-symbolic quantity. This last skill suggests the existence of an interface responsible for the mapping between a non-symbolic representation system and the verbal number system (Rousselle & Noël, 2007). Consequently, deficits in these domain-specific skills could be at the origin of subsequent difficulties in academic performance in mathematics, and may even be the cause of developmental dyscalculia (Butterworth, 2005; Castro et al., 2012; De Smedt & Gilmore, 2011; Finke et al., 2020; Inglis et al., 2011; Kolkman et al., 2013; Landerl et al., 2004; Libertus et al., 2011; Rousselle & Noël, 2007; Wong & Chan, 2019).

The second hypothesis proposes that there is a close relationship between the development of general cognitive processes and mathematical achievement, so that deficits in mathematical tasks could be explained by difficulties in non-numerical processes, such as executive functions, verbal reasoning, intellectual capacity, and attention (Aragón et al., 2019; Barnes et al., 2020; Castro et al., 2017; Castro et al., 2021; Fuchs et al., 2010; Geary, 2011; Geary et al., 2000; Geary et al., 2012; Guzmán et al., 2019; Kaufmann et al., 2013; LeFevre et al., 2013; Mammarella et al., 2021; Swanson, 2011; Szcs et al., 2013). Regarding this hypothesis, attentional networks have been much less explored compared to other processes such as working memory, and there is still little evidence on how the functioning of such networks is related to mathematical performance. In a study conducted by Poorghorban et al. (2018) in 4th graders of elementary school with low and high achievement in mathematics, the authors explored the relations between attention and mathematical abilities to determine the contribution of these processes to math performance. The results showed the low-achieving group performed significantly lower than the high-achieving group in attentional shifting. However, there was no significant difference between the two groups in executive attention.

The present study will focus on exploring whether there is a contribution of orienting (attentional shifting) and attentional control (executive attention) networks to basic arithmetic efficiency in second and third grade school-aged children, with and without difficulties in this domain of mathematics.

The attentional control network (executive attention) is a brain network related to error detection and the ability to resolve conflicts among emergent responses (Botvinick et al., 2001; Dehaene et al., 1994). Consequently, executive attention involves control processes that are instrumental in many complex cognitive tasks, including inhibition of competing responses, goal maintenance, and response selection (Engle, 2002; Kane & Engle, 2003; McCabe et al., 2010). On the other hand, the attentional orienting network is responsible for attentional shifting, i.e., the ability to shift attentional focus between sets, tasks, or strategies. It allows the disconnection of a set of irrelevant tasks and the subsequent initiation of a new, and more appropriate set (Fan et al., 2002). The ability to shift attention allows switching between operations, solution strategies, quantity ranges, stimuli presentation format (e.g., between Arabic numbers and representations of non-symbolic quantities), and between steps in a complex multi-operation problem.

A good performance in basic arithmetic tasks depends on the fluency achieved in this domain. Arithmetic fluency refers to the latency required to correctly solve arithmetic exercises with single-digit numbers, such as 3 + 4 and 8 – 5 (LeFevre et al., 2013). Continuous improvement in the access to these numerical facts reflects the degree to which children are increasingly beginning to use automatic retrieval from memory to solve arithmetic problems, rather than using counting or other counting-based solutions or other numerical procedures (Geary, 2010; Geary et al., 2012; Wu et al., 2008). This skill lies at the core of more complex mathematical procedures such as evaluation and planning of problem-solving strategies. Several studies have shown that children with difficulties in arithmetic acquire procedural skills more slowly than their peers and have a persistent deficit in number facts retrieval from long-term semantic memory (Geary, 2010; Geary et al., 2007; Kaufmann et al., 2004; Temple & Sherwood, 2002). In this regard, one of the hypotheses developed proposes that executive attention could significantly contribute to the development of arithmetic fluency (LeFevre & Kulak, 1994; Siegler & Shrager, 1984) as it is closely related to the progressive automation of numerical facts retrieval that occurs during the first years of schooling. To explain this, Siegler and Shrager (1984) use the 3 + 4 problem as an example. The authors describe that a common error among children who have to solve this problem is to answer “5”, since it is likely that the relatively strong activation of the counting sequence probably results in “5” being activated as much or more than the “3 + 4”, correct answer “7”. As schooling progresses, children develop arithmetic associations in which mental arithmetic associations between problems and possible answers become progressively stronger for correct answers and less strong for other associations. It would be expected then, that children with good inhibitory processes (as they learn arithmetic operations) would be able to inhibit irrelevant associations more quickly or completely and, therefore, they would less likely develop spurious and misleading associations. Evidence from other studies support this hypothesis, as they have found overload in the working memory system in children with arithmetic difficulties as a result of inability to inhibit irrelevant information (D’Amico & Guarnera, 2005; Gathercole et al., 2004; Passolunghi et al., 2005; Passolunghi & Pazzaglia, 2004; Passolunghi & Siegel, 2001, 2004; Swanson & Sachse-Lee, 2001). Likewise, LeFevre et al. (2013) have described that executive attention plays an important role not only in the acquisition of new procedures and automatic access to arithmetical associations, but that it is also a good predictor of arithmetic fluency in children between the second and fourth year of elementary school. In contrast, Censabella and Noël (2008) found no significant differences between children with mathematics difficulties and their control peers in the suppression of irrelevant information, suggesting difficulties in mathematics would result from specific deficits in numerical processing and not from deficits in attentional skills (such as inhibition).

Regarding attentional shifting, it has been described that it is involved in arithmetic performance, since in multi-step arithmetic problems it is required to shift between arithmetic strategies (e.g., addition, subtraction, multiplication) and arithmetic sub-solutions. Several studies have shown that children with arithmetic difficulties show this reduced ability to attentional shifting (Andersson, 2008; Bull et al., 1999; Bull & Scerif, 2001; van der Sluis et al., 2007). More recent evidence comes from two meta-analyses (Friso-van den Bos et al., 2013; Yeniad et al., 2013) in which a significant correlation between performance in mathematics and attentional shifting was found. In particular, Yeniad et al. (2013) showed attentional shifting contributes to academic performance, regardless of variations in samples and procedures used in the studies. They also pointed out a substantial association between intellectual capacity and attentional shifting, suggesting the impact of intellectual capacity should be controlled for when exploring the contribution of attentional shifting or other components of executive functioning to academic achievement in mathematics. However, results from other studies are divergent regarding the relationship between attentional shifting and mathematics achievement. Espy et al. (2004) found no contribution of attentional shifting to mathematical skills in preschoolers (6 year-olds). On the other hand, when exploring inhibition and attentional shifting in children with difficulties in mathematics and their control peers, Van der Sluis et al. (2004) also found no differences between groups. Similarly, Gold (2013) reported children with difficulties in mathematics did not differ from controls in their attentional shifting during the task.

The above review of the literature shows inconsistent results on the contribution of control and orienting attentional networks to performance in arithmetic. One of the possible reasons of inconsistencies in the findings reported is the fact that studies examining deficits in the domain-general processes’ hypothesis as the origin of difficulties in mathematics usually do not control for the contribution of basic numerical skills in their analyses, yielding results that could also be influenced by difficulties in these processes and not only by the contribution of evaluated domain-general cognitive processes.

The Present Study

This study focuses on exploring the contribution of both, basic numerical abilities and domain general cognitive processes (in particular, of the executive control and orientation attentional networks) to efficiency in basic arithmetic in second to third grade children, with and without difficulties in this domain of mathematics. The study has three specific goals: 1) to explore whether there are significant differences between children with difficulties in basic arithmetic (AD group) and their peers without difficulties (control group - CT) in specific domain skills (numerical skills: subitizing, counting, and symbolic and non-symbolic quantities comparison); 2) to explore whether there are significant differences between CT and AD groups in executive attention and attentional shifting; in contrast to previous studies, considering the demonstrated influence of basic numerical skills on later arithmetic performance (see Reigosa-Crespo et al., 2013), in this analysis we will control for the effect of numerical variables in which the groups show significant differences; 3) to analyze the specific contribution of both executive attention and attentional shifting to the explanation of variance in basic arithmetic efficiency in each group (CT and AD).

We expect that if difficulties in the AD group are only due to impairments in domain-specific variables (basic numerical skills), the results of both groups (CT and AD) would be significantly different in the tasks that assess these skills, but the groups will exhibit similar results in attentional tasks. Conversely, if attentional networks also influence efficiency in basic arithmetic, children in the AD group would exhibit significantly lower performance in the attentional networks tasks compared to the CT group, even when controlling for the effect of basic numerical skills. Finally, we hypothesize attentional processes will show a significant contribution to the explanation of individual variability in basic arithmetic efficiency.

Method

Participants

For participants’ selection we used a non-probabilistic convenience sampling in the classrooms of second and third grade of primary school of four school in the city of Santiago de Chile, Chile. The initial sample selection (182 children) was conducted using teachers’ responses to a questionnaire comprising risk indicators of difficulties in mathematical achievement for each child. Previous studies reported that a teacher’s judgments regarding mathematical ability of their students are good predictors of later academic performance (see Reigosa-Crespo et al., 2012). Children without risk indicators for mathematical difficulties were initially included in the typically achieving group (CT group). Children with at least one risk indicator for mathematical learning disabilities were initially identified as children at risk of arithmetical difficulties (AD group). After that, all children were evaluated with the Raven’s Coloured Progressive Matrices Test (Raven et al., 1992), which assesses non-verbal intellectual capacity. To be included in the sample, children had to obtain scores between the 50^th and 95^th percentiles on this test.

Finally, selected participants were evaluated using a timed mental arithmetic task (see description below). An efficiency measure (EM) was calculated for this task. EM is an inverse measure (higher values of efficiency measure represent worse performance) (for details see the Statistical Analysis section). Timed mental arithmetic tasks have been used in a number of previous studies to identify learning mathematical difficulties since they explore fluency and accuracy in calculation/numerical facts retrieval associated with simple additions and subtractions (see Butterworth, 2003; Reigosa-Crespo et al., 2012).

For the definitive inclusion in each group, we used the method proposed in Neuropsychology by Crawford et al. (2010) to compare single-case behavioural measures against an appropriate control sample. This procedure allows us to make accurate comparisons with more modest sample sizes (N), without the risk of exaggerating the abnormality of the scores, as occurs with z-value, when small samples are used. Following this method, the mean (M) of the EM obtained in the timed mental arithmetic task by the CT group was calculated. A “leave-one-out analysis” was conducted to compare each individual mental arithmetic EM against this M. Participants whose efficiency in the mental arithmetic task was significantly lower than the M of the rest of the CT group plus one standard deviation (SD) were included in the final CT group (CT: individual EM < M + 1 SD). Participants whose EM in the mental arithmetic task was larger than or equal to the M of the CT group plus 1.5 SD were included in the final AD group (AD: individual EM ≥ M + 1.5 SD). The final sample comprised 158 school children (M = 8.05 years, SD = 0.72 years). A similar procedure for sample selection was used in Castro et al. (2021) (See Table 1 for a detailed sample description).

Materials

Timed mental arithmetic task. Fifty-six items of arithmetic operations with single- Arabic digit (1-9) were presented in two blocks: 28 additions and 28 subtractions. All items were presented horizontally in “2 + 4” form. Below each item, two alternative responses, one correct and one incorrect, were simultaneously displayed. Children had to select the correct answer as quickly and accurately as possible. Each trial began with the presentation of the stimulus, which remained on screen until the participant input the answer.

Numerical skills tasks

Enumeration task. Sixty items, divided in two identical blocks of sets of dots (numerosities from 1 to 9, excluding 5) were presented on the screen. Participants had to count the dots presented and press the numerical key matching the cardinality of the set of dots displayed on the screen. The children had to select the correct answer as quickly and accurately as possible. Each trial began with the presentation of the stimulus, which remained on screen until the participant inputs the answer.

Non-symbolic comparison task. Non-symbolic comparison pairs made up of two sets of dots per item, including numerosities from 1 to 9, excluding 5. These comparison pairs varied between two magnitude ranges: subitizing (1-4) and counting (6-9). Participants had to select the largest set (or smallest depending on the instruction) as quickly and accurately as possible. To prevent children from relying on perceptual strategies focused on continuous variables, three different sets of arrays were generated: controlling for density, surface, and area. The stimuli were presented in two blocks of 30 stimuli each. Each trial began with the presentation of the stimulus, which remained on screen until the answer was input.

Symbolic comparison task. Symbolic comparison pairs including two single-digit Arabic numbers (1 to 9, excluding 5). The pairs to be compared varied between the same numerical magnitude ranges previously described in the non-symbolic comparison task. Participants had to select the largest digit (or smallest depending on the instruction) as quickly and accurately as possible. The stimuli were presented in two blocks of 30 stimuli each. Each trial began with the presentation of the stimulus, which remained on screen until the answer was input.

Attentional networks tasks

Attentional shifting task. This task consisted of 30 items presented in a single block of stimuli. Each item consisted of two white squares separated by a fixation point (red asterisk). Above the square on the left side of the screen was always displayed the question: “Is the woman happy?”, and above the square on the right side was always displayed the question: “Does the man wear glasses?”. In each trial, an image showing two human figures (both, a man and a woman) was randomly displayed in one of these white squares (to the right or the left of the fixation point). Across all trials, two features were varied and randomized between the two human figures: the presence of glasses (both wearing glasses, both without glasses, only one of them wearing glasses) and happy facial expression (both happy, both sad, one happy and the other one sad). Participants had to answer to the question displayed above the white square where the image appeared (e.g., should the image appear in the square on the left, the participant had to answer the question “Is the woman happy?”). At the bottom of the screen the words YES (on the left side) and NO (on the right side) always appeared. The participant had to press the (Z) key to answer YES and the (-) key to answer NO. Participants were instructed to respond as quickly and accurately as possible.

Executive attention task. A version of the flanker’s task proposed by Pozuelos et al. (2014) was used. In this version of the task, only the executive attention network was explored. The alert and orientation conditions of the original task were not included. The task consisted of 60 items presented in two blocks of stimuli. Stimuli consisted of the presentation of a row of five yellow fish facing the right or the left side of the screen. In half of the items, the central fish of the row was facing the same direction as the rest (congruent stimulus) and in the other half of the trials, the central fish was presented facing the opposite direction of the rest of the fish in the row (incongruent stimulus). Each stimulus was kept on screen until the participant input the response, or until 2500 ms had elapsed. Participants were instructed to respond in which direction the central fish of the row was facing (right or left), disregarding the direction of the rest of the fish was, as quickly and accurately as possible.

Procedure

Following the ethical requirements for research with human beings, written consent from all participant’s parents was obtained, and all participants provided written assent for assessments.

The assessments were conducted in a quiet room within the school. Experimental tasks were administered in two 30-40 minute sessions. In the first session, intellectual capacity was assessed and afterwards the mental arithmetic task was administered. In the second session, numerical skills tasks and attentional networks tasks were administered in a counterbalanced order.

Statistical Analysis

Performance in each task was analysed using an inverse efficiency measure (higher efficiency measure values represent worse performance) which seizes the relation between RT and accuracy. Efficiency measures (EM) were calculated by dividing the median of RT (for correct responses only) by the hits proportion in each task. EMs have been used in previous studies (Kohn et al., 2020; Landerl et al., 2004; Reigosa-Crespo et al., 2012) considering this kind of combined measures provide a more complete picture of overall performance in each task. It has been observed that children with poor numerical skills tend to adopt strategies that produce generally accurate answers, but with extremely long latencies, or only respond quickly, exhibiting short latencies, but at the cost of very low overall accuracy.

For the enumeration task two EMs were calculated: one for the items in subitizing range (1-3 dots) and one for the counting range (6-8 dots), which allowed us to have a measurement of these two numerical skills separately (subitizing and counting). Similarly, for the executive attention task, two EMs were calculated: one for congruent items and one for incongruent items. With these data, the congruency effect (EC) was calculated by subtracting the EM obtained in congruent items from the EM obtained in incongruent items (EC = incongruent EM – congruent EM).

To test for differences between groups (CT vs. AD), data obtained were included in the following analysis: a) a repeated measures ANOVA with the data of numerical skills tasks (symbolic and non-symbolic comparisons, subitizing and counting); b) a repeated measures ANOVA with the data of attentional networks tasks (attentional shifting, executive attention); c) two covariance analyses (ANCOVA), the first one with the EM in the attentional shifting task and the second one with the EM in congruent and incongruent items of the executive attention task. In both analyses, numerical variables that were significantly different between groups in the previous analysis were controlled for. Note the groups were matched by intellectual capacity during sample selection, so this variable was not included in these analyses.

To test for the specific contributions of both, executive attention and attentional shifting processes to the variance of efficiency in mental arithmetic in each group (CT and AD), a correlation analysis was performed among relevant variables. After that, hierarchical regressions were performed with the results of each group considering that when there are more than two variables that significantly correlate with each other, the correlation analysis only allows us to infer that there is shared variance among these variables, but not to ascertain the influence each of these variables has on the rest. A hierarchical regression analysis allows evaluating the unique contribution of each specific variable or predictor, controlling for the effect of other variables that are related with it and with the dependent variable.

Results

Comparisons between Groups (CT vs. AD) for Basic Numerical Skills

A repeated measures ANOVA was run including the EMs of numerical skills tasks as within-subject factor (symbolic comparison, non-symbolic comparison, subitizing, and counting) and group (CT and AD) as between-subjects factor. A group effect was found: (performance of the CT group was significantly better than the AD group) F(1, 154) = 9.989, p < .01, η_p² = .061, 95% CI [1994.22, 2390.42] and [2443.17, 2849.66] for CT and AD groups respectively. An effect of numerical skills was also found: F(3, 462) = 222.46, p < .001, η_p² = .59, 95% CI non-symbolic comparison [1165.67, 1325.16], symbolic comparison [1326.89, 1454.82], subitizing [1742.30, 2003.33], and counting [4685.05, 5651.72]. In addition, an interaction between group and numerical skills was found: F(3, 462) = 2.8341, p < .05, η_p² = .018, 95% CI for CT group non-symbolic comparison [1064.46, 1287.11], symbolic comparison [1135.45, 1314.04], subitizing [1552.87, 1917.26], and counting [3958.96, 5308.41] and 95% CI for AD group non-symbolic comparison [1200.83, 1429.26], symbolic comparison [1465.35, 1648.57], subitizing [1823.64, 2197.49], and counting [5010.83, 6395.34]. Planned comparisons showed significant differences between groups for symbolic comparison (p < .001), subitizing (p < .05) and counting (p < .05). No significant differences between groups were found for non-symbolic comparison (p = .086). See Figure 1.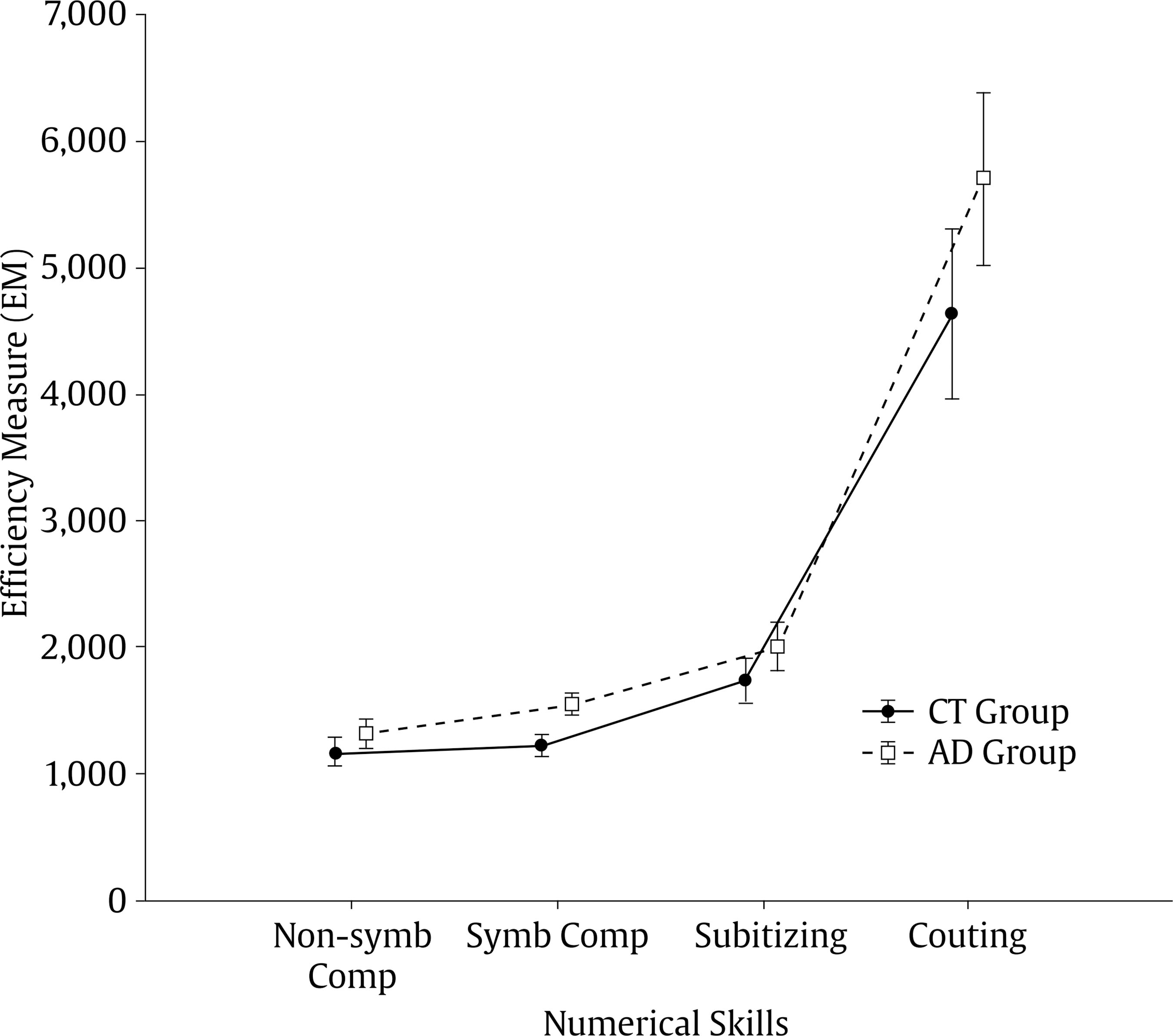

Comparisons between Groups (CT vs. AD) for Attentional Networks

A repeated measures ANOVA was run including EMs of attentional networks tasks as within-subject factor (attentional shifting, executive attention) and group (CT and AD) as between-subjects factor. A group effect was found: (performance of the CT group was significantly better than that of the AD group) F(1, 156) = 33,116, p < .001, η_p² = .018, 95% CI [1252.90, 1510.24], and [1784.78, 2045.40] for CT and AD groups respectively. An effect of attentional networks was also found: F(1, 156) = 812,05, p < .001, η_p² = .84, 95% CI attentional shifting [2643.05, 2929.73] and executive attention [417.17, 603.38]. In addition, an interaction between group and attentional networks was found: F(1, 156) = 9,6143, p < .01, η_p² = .058, 95% CI for CT group attentional shifting [2194.38, 2597.22] and executive attention [236.51, 498.19] and 95% CI for AD group attentional shifting [2972.99, 3380.97] and executive attention [520.70, 785.71]. Planned comparisons showed significant differences between groups for attentional shifting (p < .001) and executive attention (p < .01).

Comparisons between Groups (CT vs. AD) for Attentional Networks Controlling for Basic Numerical Skills

Attentional shifting. An ANCOVA was run with the EM of attentional shifting task as the within-subject factor, group (CT and AD) as between-subjects factor and numerical skills (subitizing, counting, and symbolic comparison) as covariates. A group effect was found (performance of the CT group was significantly better than the AD group): F(1, 151) = 11.075, p < .001, η_p² = .068, 95% CI [2206.03, 2585.57] and [2980.42, 3369.82] for CT and AD groups respectively.

Executive attention. An ANCOVA was run with EMs of the executive attention task as the within-subject factor (EM of incongruent items and EM of congruent items), group (CT and AD) as between-subjects factor, and numerical skills (subitizing, counting and symbolic comparison) as covariates. A group effect was found (performance of the CT group was significantly better than the AD group): F(1, 151) = 17.376, p < .001, η_p² = .103, 95% CI [805.48, 971.14] and [1112.99, 1282.95] for CT and AD groups respectively. A congruency effect was also found: F(1, 151) = 4.755, p < .05, η_p² = .030, 95% CI [753.14, 819.13] and [1197.96, 1402.32] for congruent and incongruent items respectively. In addition, interaction between group and congruence was found: F(1, 151) = 6.644, p < .01, η_p² = .042, 95% CI [658.58, 750.69] and [929.34, 1214.61] for congruent and incongruent items respectively in the CT group and 95% CI [820.39, 914.89] and [1381.967, 1674.65] for congruent and incongruent items respectively in the AD group. Planned comparisons showed congruency effect for both groups (p < .001 in both cases). However, the CT group showed significantly better efficiency compared to the AD group both in congruent and incongruent items (p < .001 in both cases). See Figure 2.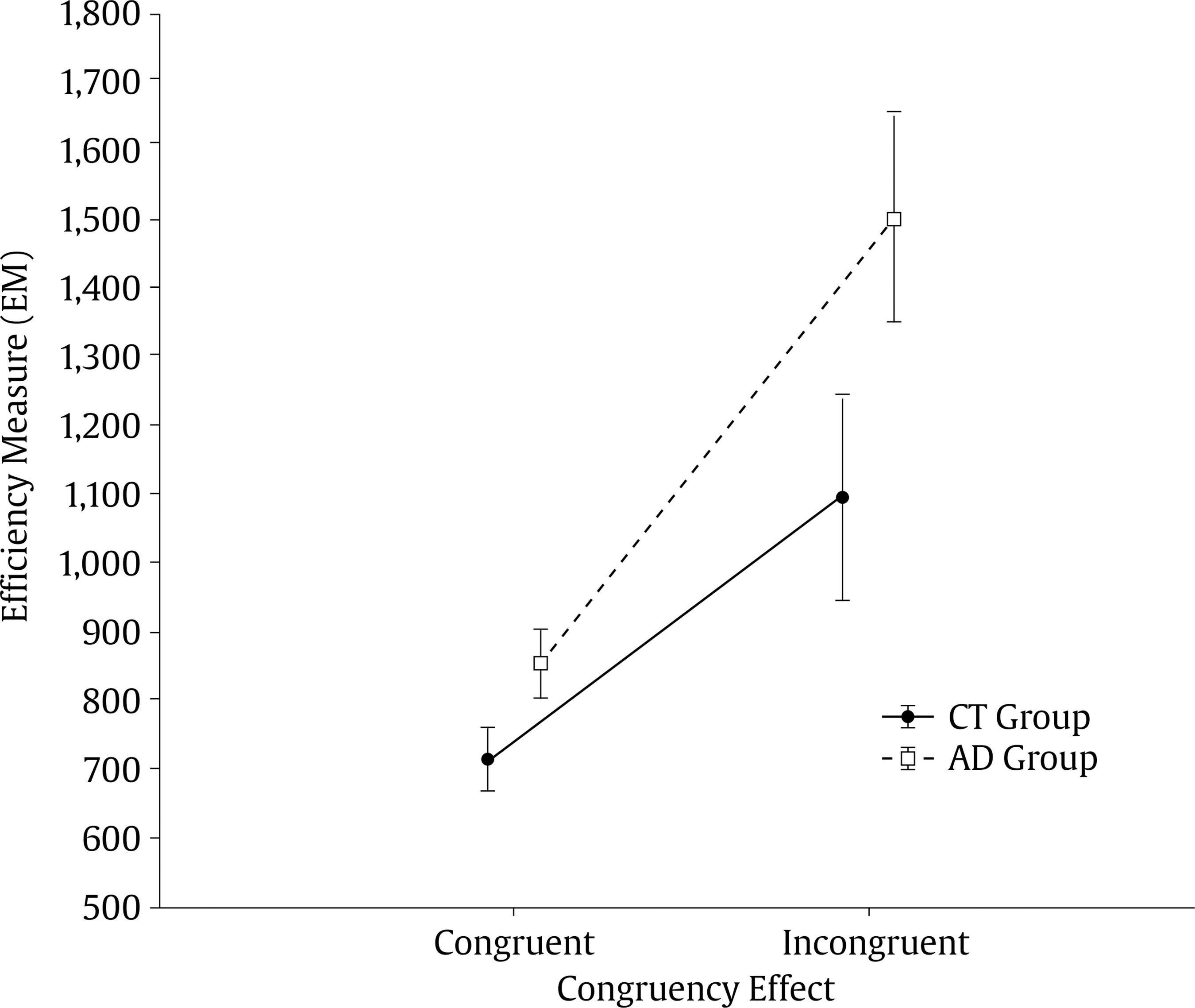

Hierarchical Regressions

Correlations among efficiency in basic arithmetic, numerical skills and attentional networks. This analysis showed a different pattern of correlations for each group. Details are shown in Table 2.

Hierarchical regressions: CT group. The full model of this hierarchical regression (variables from both blocks 1 and 2) explained 27.6% (R² = .276) of the variance in basic arithmetic efficiency: F(4, 75) = 7.139, p < .001. Between covariates included only symbolic comparison showed a significant contribution to individual variability in basic arithmetic efficiency: B = 3.430, p < .001, 95% CI [1.604, 5.255]. No significant contribution of attentional shifting to arithmetic efficiency was found: F(1, 75) = 1.498, B = 0.566, p = .225, 95% CI [-.355, 1.487]. See details in Table 3.

Hierarchical regressions: AD group. Full models of this hierarchical regression (variables from both blocks 1 and 2) explained 21.7% (R² = .217) of the variance of efficiency in basic arithmetic: F(3, 74) = 8.095, p < .001. The covariate included (efficiency in non-symbolic comparison) and attentional shifting showed no specific contribution in this analysis. On the contrary, the congruency effect (executive attention) showed a significant contribution to the individual variability in basic arithmetic efficiency: 11.0 % (R² = .110), F(1, 74) = 10.805, B = 1.850, p < .01, 95% CI [.728, 2.971]. See details in Table 4.

Discussion

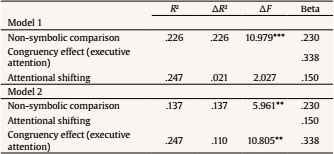In this study, we explored the contribution of executive attention and attentional shifting to arithmetic achievement in second to third grade elementary school children, with and without difficulties in this domain of mathematics, by comparing between groups CT vs. AD in tasks assessing numerical skills and attentional networks. As expected, an association between basic numerical skills and arithmetic achievement was confirmed in the studied sample in line with previous reports cited in the introduction. Comparisons in basic numerical abilities between CT and AD groups showed the AD group had a significantly lower performance compared to the control group. Particularly, the interaction found between group and numerical skills suggests the AD group struggled with tasks relying in the association between quantities and the corresponding numerical symbols, whereas their efficiency in non-symbolic comparisons did not differ from the control group. These results suggest AD children would have difficulties in the development of the interface responsible for the mapping between the non-symbolic representation system and the verbal number system.

Regarding attentional networks, the AD group showed a significantly lower performance compared to the control group in terms of both attentional shifting and in executive attention efficiency measures. These results support the hypothesis of a contribution of domain-general cognitive processes to arithmetic performance and are consistent with previous studies reporting a lower ability to shift attention (Bull et al., 1999; Bull & Scerif, 2001; van der Sluis et al., 2007) and a deficient attentional control (LeFevre et al., 2013; LeFevre & Kulak, 1994; Siegler & Shrager, 1984) in children with arithmetic difficulties.

The analysis of the specific contribution of attentional shifting and executive attention to the explanation of individual variability in arithmetic efficiency leads to interesting findings. First, when analyzing correlations between basic arithmetic, numerical skills, and attentional networks, the correlations matrices found were different between groups. In the control group significant correlations between basic arithmetic and subitizing, symbolic comparison and counting (skills that require the use of numerical symbols), and attentional shifting (although this attentional network did not show a significant contribution to the explanation of the variance of arithmetic efficiency in this group) were found. In contrast, in the AD group there were confirmed significant associations between basic arithmetic and both attentional networks (attentional shifting and executive attention) and only a significant correlation between basic arithmetic and non-symbolic comparison. Furthermore, in this group, executive attention showed a significant contribution to the explanation of variance in basic arithmetic efficiency of 11.0%. This analysis by group stems from previous reports of different patterns of brain activation found when comparing children with difficulties in number processing and typically developing children (De Smedt et al., 2011) and also when comparing children and adults (Kawashima et al., 2004). These studies suggest the activation of brain networks involved in executive processes, in addition to those specialized in numerical cognition, reported in younger children and subjects with developmental dyscalculia reflects the activation of compensatory mechanisms elicited in response to high cognitive demands posed by the tasks. The present study tries to explore at behavioral level the presence of these compensation mechanisms in the sample studied, through the comparison of correlation matrices between variables evaluated in AD and control groups. The results reported here are in line with the aforementioned neuroimaging evidence and suggest efficiency in basic arithmetic in children with difficulties in this domain is supported by the interplay of domain-specific numerical skills and (potentially compensatory) domain-general cognitive mechanisms.

Performing basic arithmetic computations requires a sequence of cognitive operations (which vary depending on the complexity of computation), but in general it includes representation and short-term storage and manipulation of numerical information and of the corresponding operational sign, access to and retrieval of numerical facts and arithmetic procedures from long-term memory, and finally computation and production of a response. The results presented here suggest that typically developing children achieve increasing automation of number fact retrieval and numerical information manipulation, which leads to fluent resolution of basic arithmetic problems with very little demand of attentional resources. In contrast, children with low performance in arithmetic have been described as presented with persistent difficulties in number facts retrieval, which in turn hinders arithmetic fluency (Geary, 2010; Geary et al., 2007; Kaufmann et al., 2004; Temple & Sherwood, 2002). These previous findings, together with deficits in the recognition of numerical symbols in the AD group pointed out here and the significant correlation between non-symbolic comparison and arithmetic in this group, suggest AD children may be relying on much more immature strategies for solving arithmetic problems (such as counting-all, using concrete representations, or manipulative: counting with fingers, etc.). These strategies would demand much more attentional control and could account for the significant implication of attentional networks in arithmetic in the AD group, compared to that of their peers without difficulties. Such a relation between high levels of executive attention and development of arithmetic fluency has been previously reported by LeFevre et al. (2013). In summary, the above said suggests children with arithmetic difficulties recruit attentional resources to a greater extent, but at the same time achieve lower efficiency levels than their typically developing peers in attentional tasks. Hence, it supports the hypothesis that their difficulties in arithmetic would originate from a double deficit both, in numerical and attentional brain networks.

Conclusions

Findings of the present study support deficits in both basic numerical abilities and domain general processes contribute to the origin of difficulties in arithmetic: 1) children with difficulties in basic arithmetic showed deficits in basic numerical abilities consistent with damage in an interface specialized in the mapping between the non-symbolic representation system and the verbal number system, which results in lower achievement in tasks that require the processing of numerical symbols, and 2) children with difficulties in basic arithmetic showed significantly lower performance than the control group in attentional networks tasks, which supports the specific contribution of domain-general processes to arithmetic achievement. All results considered, arithmetic difficulties seem to result not only from deficits in core numerical skills, but rather from a heterogeneous combination of deficits, particularly including difficulties in attentional processing. Though interesting, the findings presented here should be interpreted with caution and subsequent studies should be performed in order to shed light on the contribution of each attentional network. Also, experimental designs including parametric manipulations of both, attentional and arithmetic tasks, are advisable. Additionally, in this study only children in second to third year of elementary school were assessed. Finally, future studies should focus on exploring the interplay between the developmental trajectories of different domain-general cognitive processes and core numerical processes across all grades of elementary education and explore the impact of these interactions in mathematics achievement.