
Interés de los Futuros Maestros en Saber Crear Problemas de Matemáticas para Enseñar a Resolverlos
[Pre-service teacher´ interest in posing mathematics problems to teach students to solve them]
Alberto Mallart-Solaz
Universidad de Barcelona, España
https://doi.org/10.5093/psed2018a17
Recibido a 24 de Enero de 2018, Aceptado a 27 de Mayo de 2018
Resumen
Las habilidades para crear problemas de matemáticas y para resolverlos están relacionadas. Este estudio pretende averiguar si los futuros maestros consideran las habilidades creativas útiles para enseñar la resolución, con la hipótesis de que se practica poco la creación. La muestra la constituyen 94 futuros maestros de la Universidad de Barcelona. Se ha investigado qué características consideran importantes en los problemas de matemáticas, qué relación encuentran entre crearlos y resolverlos y qué habilidades creativas han desarrollado. Los primeros resultados muestran que desconocen las características, no conciben la creación y resolución como procesos diferentes y creen estar bien preparados para crearlos. Se introduce un mecanismo didáctico mostrando la utilidad de crearlos para enseñar la resolución. Los segundos resultados muestran falta de práctica en crearlos y desconocimiento en crear problemas con fines educativos. Se concluye que los futuros maestros no contemplan el crear problemas como herramienta para enseñar a resolverlos por falta de práctica.
Abstract
Skills of posing math problems are related to problem-solving skills. This research aims to know if pre-service teachers consider problem-posing skills are useful to teach problem-solving, starting from the hypothesis that there is little practice in problem-posing. The participants were 94 pre-service teachers of the University of Barcelona. This study points at the most important characteristics of mathematics problems for them, the relations between problem-posing and problem-solving, and which problem-posing skills they have developed. First findings they do not know relevant characteristics of mathematics problems, they do not consider posing and solving problems two different processes, and they think they are well prepared to pose problems. An educational tool is introduced to the usefulness of problem-posing to teach students problem-solving. Second findings a lack of practicing in problemposing and that teachers do not know how to pose problems for educational purposes. So, pre-service teachers do not consider problem posing a tool to teach problem-solving due to lack of practicing.
Palabras clave
Creación de problemas, Resolución de problemas, Futuros maestros de matemáticas, Didáctica de las matemáticas.
Keywords
Problem-posing, Problem-solving, Pre-service mathematics, teachers, Mathematics education.
Para citar este artículo: Mallart-Solaz, A. (2018). Interés de los futuros maestros en saber crear problemas de matemáticas para enseñar a resolverlos. Revista Psicología Educativa, 25, 31-41. https://doi.org/10.5093/psed2018a17
Correspondencia: alberto.mallart@gmail.com (A. Mallart Solaz).
Introducción Muchos autores muestran que existe una fuerte relación entre la creación de problemas con fines didácticos (conocido con el término de problem-posing) y su resolución (conocido con el término de problem-solving). Silver y Cai (1996) estudiaron la relación entre el problem-posing y el problem-solving y sus conclusiones fueron que el éxito en la resolución de problemas estaba fuertemente correlacionado con el éxito en la creación de problemas. En este estudio de Silver y Cai (1996) se observa que el problem-posing no sólo implica la formulación de nuevos problemas, sino que también implica la reformulación de situaciones dadas. Observemos que un docente podría crear problemas mientras los está resolviendo, haciendo pequeñas modificaciones que ayuden a la comprensión de la resolución. También puede reformular un problema para reducir la medida de los números implicados o para estudiar casos particulares de la situación dada para mejorar la comprensión del problema (Silver, 1994). English (1997) estudió las actividades cognitivas en creación de problemas examinando los procesos implicados. Estableció que para ser capaz de crear un problema con fines didácticos se requiere un amplio marco de conocimientos y se debe entender qué es un problema, reconocer su estructura (tal como la define Holyoak y Koh, 1987) e identificar estructuras similares (recuperación de análogos potencialmente relevantes como expresa Keane, 1988). Leung y Silver (1997) subrayaron el valor del problem-posing para mejorar las habilidades del problem-solving, mostrando que la creación de problemas influenciaba positivamente en el desarrollo de las estrategias de resolución. Kesan, Kaya y Güvercin (2010) estudiaron la influencia del problem-posing en el desarrollo de las habilidades matemáticas. Espinoza, Lupiáñez y Segovia (2014) estudiaron alumnos con talento y la creación de problemas y mostraron que los problemas creados contenían enunciados más largos y más preguntas y que el número de procesos y pasos implicados en la resolución era mayor que en los problemas creados por un grupo estándar. Espinoza et al. (2014) mostraron diferencias en las estructuras semánticas y en la cantidad de relaciones semánticas implicadas en la resolución de problemas entre un grupo de estudiantes con talento y otro ordinario. No debemos olvidar tampoco que la creatividad (en especial, en resolución de problemas) en los niños es diferente de la de un adulto debido a los diferentes mecanismos psicológicos involucrados, el grado de control sobre el proceso creativo y la calidad de los productos ofrecidos en cada etapa (Romo, Alfonso-Benlliure y Sánchez-Ruiz, 2016). En el caso del futuro docente adulto conviene tener en cuenta a Sternberg (1988) cuando define tres metacomponentes cognitivos del proceso creador: reconocimiento de la existencia de un problema, definición del problema y formulación de una estrategia o representación mental para su solución. El presente estudio se propone conocer lo conscientes que son los futuros maestros de la importante relación que existe entre el problem-posing y el problem-solving (tal como prueban Leung y Silver, 1997; Silver y Cai, 1996) y cuánto les ayudaría como docentes desarrollar las habilidades del problem-posing para enseñar a resolver problemas a sus futuros alumnos con diferentes enfoques. En realidad, estas dos pretensiones no son independientes, dado que la consciencia de la importancia de la relación puede valorarse a través de su capacidad para ayudar a enseñar a resolver problemas. Brown y Walter (2005) establecieron que el problem-posing es una manera de explorar la propia comprensión y elaborar cuestiones que pueden ayudar a evaluar para dominar contenidos matemáticos. Los futuros maestros deberían practicar las habilidades del problem-posing, por lo menos reformulando enunciados con propósitos didácticos (Rowland, Huckstep y Thwaites, 2003). Los futuros maestros reconocen la importancia del problem-posing, pero alegan haber tenido pocas oportunidades para practicar (Ellerton, 2013). La atención se ha centrado en las habilidades de resolver problemas y no en las habilidades de crearlos (Crespo, 2003). Como resultado, muchos maestros no parecen haber desarrollado las habilidades de problem-posing (Pelczer y Gamboa, 2008; Singer, Ellerton, Cai y Leung, 2011). Siguiendo esta idea amparada por estos nueve autores, este estudio se propone averiguar lo que piensan sobre sus propias habilidades a la hora de crear problemas y si se sienten cómodos con el problem-posing. Desde la perspectiva de la enseñanza, la creación de problemas es una herramienta útil porque permite al docente comprender mejor los procesos cognitivos de los estudiantes (English, 2003). Reconociendo una cierta falta de práctica en el problem-posing, según los autores mencionados, se puede considerar el modelo llamado cuarteto del conocimiento (KQ) propuesto por Rowland et al. (2003). Este modelo observa el conocimiento didáctico del maestro del contenido matemático, considerando 4 dimensiones: 1) los precedentes teóricos o fundamentos y las creencias de los futuros maestros (lo que aprenden en su preparación para ser un maestro), 2) la capacidad del maestro para transformar el conocimiento del contenido y adaptarlo a los estudiantes (usando recursos, seleccionando representaciones y proponiendo ejemplos), 3) la coherencia de las explicaciones y sus conexiones con las tareas y ejercicios puestos y 4) situaciones que ocurren en la clase difíciles de planificar (habilidades para responder situaciones no planificadas). Este modelo refleja explícitamente la importancia de las habilidades del maestro para adaptar la dificultad de un problema nuevo creado al grupo de resolutores. En cuanto al punto 2, es necesaria su habilidad y capacidad para adaptar los conocimientos y dificultades a sus alumnos. En cuanto al punto 3, es necesaria su habilidad para mantener un hilo argumental consistente y coherente. En cuanto al punto 4, es necesaria una capacidad adecuada de reacción ante situaciones emergentes para recalibrar la dificultad planteada. Aparte de las matemáticas que permiten resolver una tarea propuesta, los maestros han de conocer diferentes representaciones del mismo objeto matemático, diferentes procesos para resolver una tarea, diferentes relaciones entre los objetos matemáticos del mismo nivel educativo u otros, diferentes justificaciones y explicaciones y la detección del conocimiento implicado en la resolución (Pino-Fan y Godino, 2015). La creación de problemas adecuados satisfaciendo los objetivos curriculares constituye una herramienta útil para enseñar a resolver problemas (Mallart, Font y Malaspina, 2016). Objetivos Este estudio se ha desarrollado en un contexto de geometría, donde puede llevarse a cabo la experimentación, la elaboración de conjeturas y su comprobación (Yerushalmy, Chazan y Gordon, 1990). A pesar de conocerse la relación entre la creación de problemas y la resolución de los mismos, nos interesa saber por qué muchos maestros no han desarrollado habilidades en crear problemas, tal como manifiestan Pelczer y Gamboa (2008) y Singer et al. (2011). El objetivo general es averiguar si los futuros maestros consideran importante que el docente sepa crear problemas para disponer de un recurso didáctico efectivo en la enseñanza de la resolución de problemas. Para responder a esta cuestión, hemos formulado tres objetivos específicos: a) investigar a qué le dan importancia y a qué no sobre los problemas de matemáticas, b) investigar qué relaciones encuentran entre el problem-posing y el problem-solving y c) investigar qué habilidades del problem-posing han desarrollado. Además, proponemos un mecanismo didáctico para mostrar la utilidad de la creación de problemas para enseñar su resolución, tras una reflexión. Estos objetivos planteados están encaminados a aceptar o rechazar la hipótesis de trabajo de que en la enseñanza preuniversitaria no se trabaja suficiente el problem-posing y ello contribuye a que los futuros maestros no lo tengan en consideración para enseñar a resolver problemas. Si se consigue averiguar qué habilidades del problem-posing han desarrollado (tercer objetivo) y cuáles no, se podrá incidir en las carencias para solventarlas en cursos de formación del profesorado, por lo cual es necesario más evidencia al respecto. Saber crear problemas es importante para instruir la resolución de los mismos, según expresan múltiples autores anteriormente citados (Mallart et al., 2016; English, 2003; Leung y Silver, 1997; Pino-Fan y Godino, 2015). La resolución de problemas es una cuestión de habilidad práctica y como tal, se adquiere mediante la imitación y la práctica. El profesor que desee desarrollar en sus alumnos la aptitud para resolver problemas, debe crear el mayor número posible de ocasiones de imitación y práctica (Polya, 1970). MétodoParticipantes La muestra consistió en 94 estudiantes de magisterio que cursaban la asignatura obligatoria de didáctica de la geometría de tercer curso, en la Universidad de Barcelona. Al comenzar el curso se constata que salvo 5 alumnos, el resto tienen aprobada la asignatura obligatoria de razonamiento matemático, impartida en segundo curso. La mayoría también expresa que, a pesar de haberla aprobado, tienen la necesidad de aprender a enseñar a resolver problemas de matemáticas. Esta investigación se llevó a cabo durante el curso académico. Instrumentos Los instrumentos de recolección usados estuvieron en función del tipo de información requerida: cuestionarios, diario de campo, producciones de los alumnos y registros en el moodle de la asignatura. Para justificar la relevancia y representatividad del contenido de los cuestionarios primero (Q1) y segundo (Q2) que se detallarán a continuación, se ha utilizado la triangulación de expertos llevada a cabo por un catedrático de didáctica y un profesor titular de didáctica de las matemáticas, ambos con más de veinte años de experiencia. Tabla 1 Cuestionario 1 (Q1) sobre las características de un problema, requisitos para saber crearlos y utilidad para enseñar a resolverlos  Tabla 2 Cuestionario 2 (Q2) sobre las características presentes y no presentes de los problemas que los mismos participantes han creado  El primer cuestionario abierto (Q1, Tabla 1) formula 10 preguntas, donde esencialmente pregunta las características de un problema, requisitos para saberlos crear, ventajas de saberlos crear cuando se enseñan matemáticas en una clase de primaria, ventajas de practicar el crear problemas en la Facultad de Educación, diferencias y semejanzas entre crear problemas y solucionarlos y, por último, les pregunta cómo puede ayudar el saber crear problemas a la hora de evaluar. La décima pregunta del cuestionario propone la creación y solución de dos problemas de geometría para alumnos del último curso de primaria (12 años) donde apareciera, además de un triángulo, otro polígono. El segundo cuestionario abierto (Q2 expuesto en la Tabla 2) consta de 5 preguntas, donde la primera ofrece la oportunidad de modificar sus problemas iniciales y convertirlos en problemas que cumplan las características del listado del segundo artículo leído (Mallart et al., 2016). La segunda y tercera pregunta del cuestionario invitan a una reflexión sobre las características más y menos importantes de implementar en sus problemas. La cuarta pregunta les hace reflexionar sobre el grado de dificultad que tiene crear problemas frente a de resolverlos y la quinta pregunta hace referencia a si necesitan formarse en la creación de problemas. Variables Los cuestionarios se analizaron cualitativamente. Se identificaron tres conjuntos de indicadores: a) los referidos a los rasgos de los problemas, b) los referidos a la relación entre problem-posing y problem-solving y c) los referidos a las habilidades del problem-posing. Debajo se muestra una tabla detallada (Tabla 3) para los tres grupos de indicadores donde se especifican las cuestiones que los caracterizan. Tabla 3 Conjunto de indicadores y cuestiones dónde se califican  El primer conjunto de indicadores estudió las características más importantes de un problema para los futuros maestros y el orden de importancia. Éstas se pueden analizar a partir de las respuestas dadas a las preguntas primera y décima del Q1 y primera y segunda del Q2. El orden de importancia se puede analizar a partir de las respuestas dadas a la pregunta tercera del Q2 y al resultado de la tarea 4. También, para analizar con mayor profundidad las características de un problema, se creó un indicador cuantitativo de concordancia que muestra la congruencia entre las veces que se mencionan una propiedad y la prioridad que le otorgan. Este indicador se creó con los datos ya recogidos de la cuarta tarea, a partir de la Tabla 4 (se muestra en la Tabla 5). Tabla 4 Listado de las características de un problema ordenadas según el porcentaje de alusiones, que refleja el valor promedio de la importancia concedida 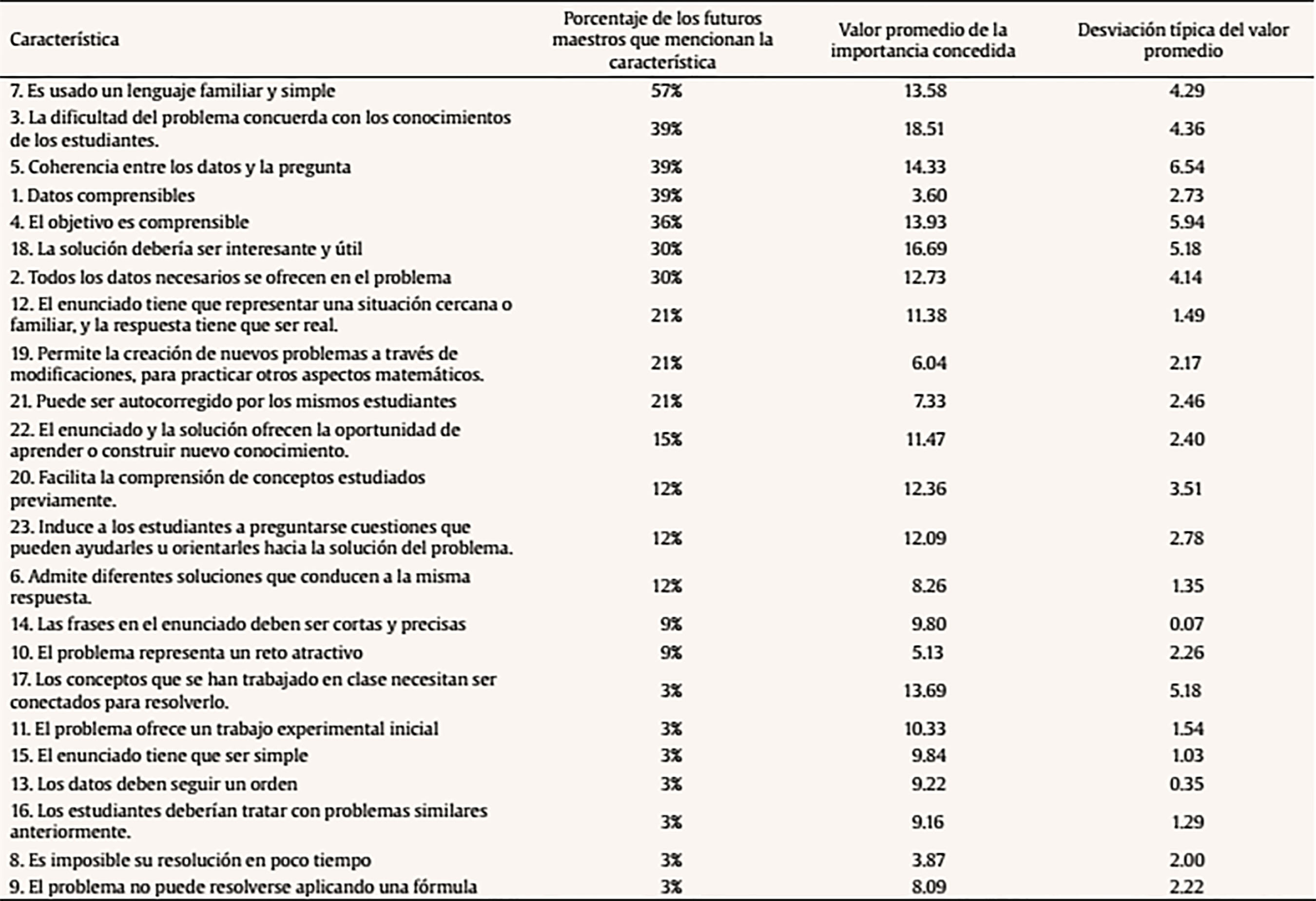 Tabla 5 Indicador de concordancia entre el número de veces mencionadas las características de los problemas y la prioridad otorgada 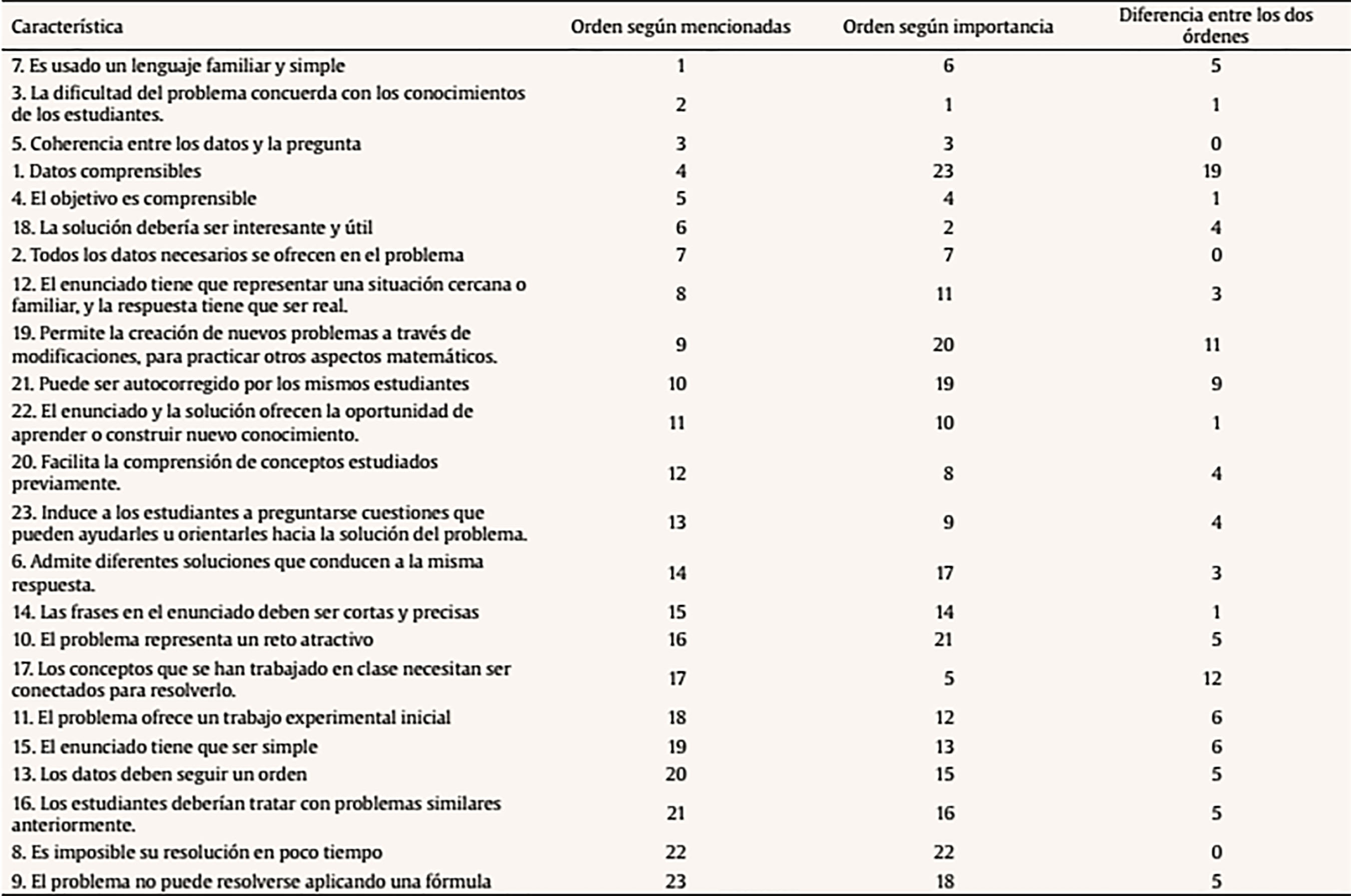 El segundo conjunto de indicadores se centró en la perspectiva conjunta de los futuros maestros sobre crear problemas y resolver problemas y en las ventajas de saber crear problemas, como muestra la Tabla 3. Las características de la creación de problemas, junto con la resolución de los mismos, que consideran los futuros maestros de matemáticas se pueden analizar a partir de las respuestas dadas a las preguntas cuarta, quinta y octava del Q1 y cuarta del Q2. Las ventajas de saber crear problemas para los futuros maestros se pueden analizar a partir de las respuestas a las preguntas segunda, tercera y novena del Q1. El tercer conjunto de indicadores se centró en lo que los futuros maestros consideran como requisitos necesarios para crear problemas y la utilidad de crearlos y en las características de los problemas creados. Además, se presta atención a las habilidades desarrolladas para la creación de los problemas. Los requisitos para crear problemas según los futuros maestros se pueden analizar a partir de las respuestas a las preguntas sexta y séptima del Q1. La utilidad que los futuros maestros ven a crear problemas se puede analizar a partir de las respuestas a las preguntas segunda, tercera, quinta y novena del Q1 y a la pregunta quinta del Q2. Las características de los problemas Q1 y a la pregunta quinta del Q2. Las características de los problemas creados se pueden analizar con sus creaciones (décima pregunta del Q1) y sus revisiones (primera pregunta del Q2). Esto se muestra en la Tabla 3. Analizando e interpretando los grupos de indicadores propuestos, es posible dar respuesta a los objetivos específicos planteados. Más concretamente, el primer grupo de indicadores, junto con el indicador cuantitativo de coeficiente de concordancia, ayudará a responder el primer objetivo, el segundo grupo de indicadores ayudará a responder el segundo objetivo y el tercer grupo ayudará a responder el tercer objetivo. Diseño La lógica que sigue el diseño de esta investigación responde a múltiples aspectos. Un primer aspecto fue la longitud de la secuencia (hojas de trabajo), que fue de cuatro tareas y que se explicará con más detalle en el siguiente párrafo. Un segundo aspecto fue el tipo de requerimiento, diferente según la tarea: a) expresión de opiniones sobre las características más importantes de los problemas de matemáticas, sobre las ventajas, utilidades y requisitos para crear problemas y sobre la relación entre crear y resolver problemas (tareas 1, 3, 4), b) creación de problemas del ciclo superior de primaria (tareas 1 y 3), c) resolución de problemas creados por ellos mismos (tareas 1 y 3), d) análisis de la actividad matemática necesaria para resolver un problema (tareas 1, 3 y 4) y e) lectura de artículos (tarea 2). Observemos que para conocer cómo piensan, lo que creen y lo que pueden crear es necesario presentarles estos cuestionarios abiertos (tareas 1, 3 y 4), en los cuales, a pesar de preguntarles cosas concretas, se les permite cierta libertad en la respuesta. Un tercer aspecto fue considerar los tres objetivos específicos que determinaron la elección de indicadores: a) un conjunto referido a los rasgos de los problemas, b) un indicador de concordancia entre las características consideradas como importantes y sus prioridades, c) un conjunto referido a las relaciones entre problem-posing y problem-solving y d) un conjunto referido a las habilidades en el problem-posing. Analizando estos indicadores, era posible dar respuesta a los objetivos específicos planteados. Señalemos que la elección de estos indicadores responde a la voluntad de analizar los resultados cualitativamente sobre sus pensamientos. Un cuarto aspecto fue tomar en consideración el entorno matemático de las tareas, que fue la geometría plana del último ciclo de primaria y los procesos de creación y resolución de problemas; este contexto es uno de los más propicios para mostrar procesos matemáticos creativos. El quinto aspecto fue contemplar la organización del trabajo que fue individual. La primera tarea consistió en contestar el cuestionario Q1 (Tabla 1), cuya pretensión era provocar que los futuros maestros pensaran en la resolución de problemas como un objetivo de enseñanza. Dispusieron de 2 horas. La segunda tarea consistió en proporcionar a los alumnos dos documentos, elaborados por investigadores en didáctica de las matemáticas (Mallart et al., 2016; Xavier de Mello, 2000). El primer artículo trataba de cómo enseñar y aprender matemáticas a partir de problemas y el segundo reflexionaba sobre el significado de un buen problema. Ambos trataban de las características de los problemas y ayudaban a los futuros maestros a ampliar el espectro de respuestas desde el punto de vista del docente. Salazar (2015) expone que pensar en la intención del creador del problema es una actividad interesante para el futuro docente. A partir de estas lecturas se les solicitó las tareas 3 y 4. La tercera tarea consistió en contestar el cuestionario Q2 (Tabla 2), cuya pretensión era propiciar una toma de conciencia de la intencionalidad que esconde resolver un problema desde el punto de vista del creador. Dispusieron de 2 horas. La cuarta tarea consistió en confeccionar un listado ordenado según el grado de importancia que otorgaban a todas las características consideradas en el segundo artículo leído (Mallart et al., 2016). La labor de ordenar un listado formado por 23 características era compleja, pero de manera organizada y con tiempo (2 horas) la podían realizar exitosamente y la información que se podía extraer era de gran riqueza. Se puntuó cada ítem en cada lista ordenada de los participantes. A la característica que ocupaba la primera posición se le otorgaron 23 puntos y así hasta la última, que recibió 1 punto. Finalmente, los puntos que cada característica obtuvo en todas las listas ordenadas fueron promediados. Calculamos el promedio para mantener el rango de valores (desde 1 hasta 23 puntos). También se calculó la desviación típica del promedio obtenido. ResultadosA continuación, se distinguirán cuatro apartados que corresponden a los 3 objetivos y al mecanismo didáctico propuesto. Por tratar con cuestionarios abiertos, hay respuestas que han ayudado a caracterizar más de un indicador, tal como se ha indicado en la Tabla 3. Características de los Problemas de Matemáticas El primer grupo de indicadores, los rasgos de los problemas, engloba tanto las características de los problemas como el orden de importancia de las mismas desde el punto de vista de los futuros maestros. Se ha hecho un análisis cuantitativo y cualitativo de los datos conjuntamente porque no sólo se ha examinado el porcentaje de alumnos que mencionan una característica y los valores promedios de cada característica (Tabla 4), sino que también se han analizado las respuestas más interesantes. La mayoría de los futuros maestros consideraron que un problema debía usar un lenguaje simple y familiar (57%). Además, muchos pensaron que la dificultad de los problemas debía ser la adecuada para los conocimientos de los estudiantes y tenía que haber coherencia entre los datos ofrecidos y pedidos (39%). Muchos futuros maestros añadieron que el objetivo debía ser inteligible, con una solución útil e interesante (30%). Aquí mostramos un ejemplo de enunciado que representa una situación cercana, porque ellos juegan a básquet cada día, usando un lenguaje cotidiano, con un grado de dificultad adecuado (participante 1): “Un grupo de estudiantes están jugando a básquet y de repente, el balón queda encajado en el aro. Entonces los estudiantes tienen que comprar otro más pequeño. Pero primero tendrán que averiguar el área del aro. Ellos saben que el diámetro es 50 cm. Calcula el área del aro y dibuja la situación”. Podemos ver que no está bien planteado porque no se ha de calcular el área del aro sino el máximo área del agujero delimitado por el aro. Aunque la utilidad de la respuesta pueda ser criticable, el objetivo es muy fácil de comprender y la conexión entre los procesos matemáticos y su vida cotidiana es evidente. Podemos ver otra característica importante señalada por ellos: el problema posibilita la creación de nuevos problemas con modificaciones (21%). En la cuarta tarea, se pidió a los futuros maestros que ordenaran un listado de 23 características de un problema de acuerdo con sus preferencias (del segundo artículo de Mallart et al., 2016). En la Tabla 4, la tercera columna muestra el valor promedio correspondiente de las características ubicadas en la primera columna y la cuarta columna la desviación típica del valor promedio. Los futuros maestros consideraron las siguientes características más importantes: a) la primera, que la dificultad fuera adecuada a los conocimientos (promedio 18.51), b) la segunda, que la solución debía parecer útil e interesante (promedio 16.69) y c) la tercera, que debe haber coherencia entre los datos ofrecidos y los pedidos (promedio 14.33). A continuación mostramos un ejemplo de un problema con un dibujo (Figura 1) y su solución (Figura 2), que tiene en cuenta estos tres aspectos (participante 2): a) la dificultad es adecuada pues plantea encontrar un recorrido de cien metros a partir de un mapa de calles (segmentos rectilíneos) y una glorieta (circunferencia) donde se indica la longitud de cada elemento, b) la solución resulta interesante porque en la asignatura de educación física se practican las carreras de distancia de cien metros y c) existe coherencia entre los datos que se facilitan (dibujo y medidas) y lo que se pide (un recorrido de cien metros). Figura 1 Ejemplo de problema que tiene en cuenta las tres características más importantes. 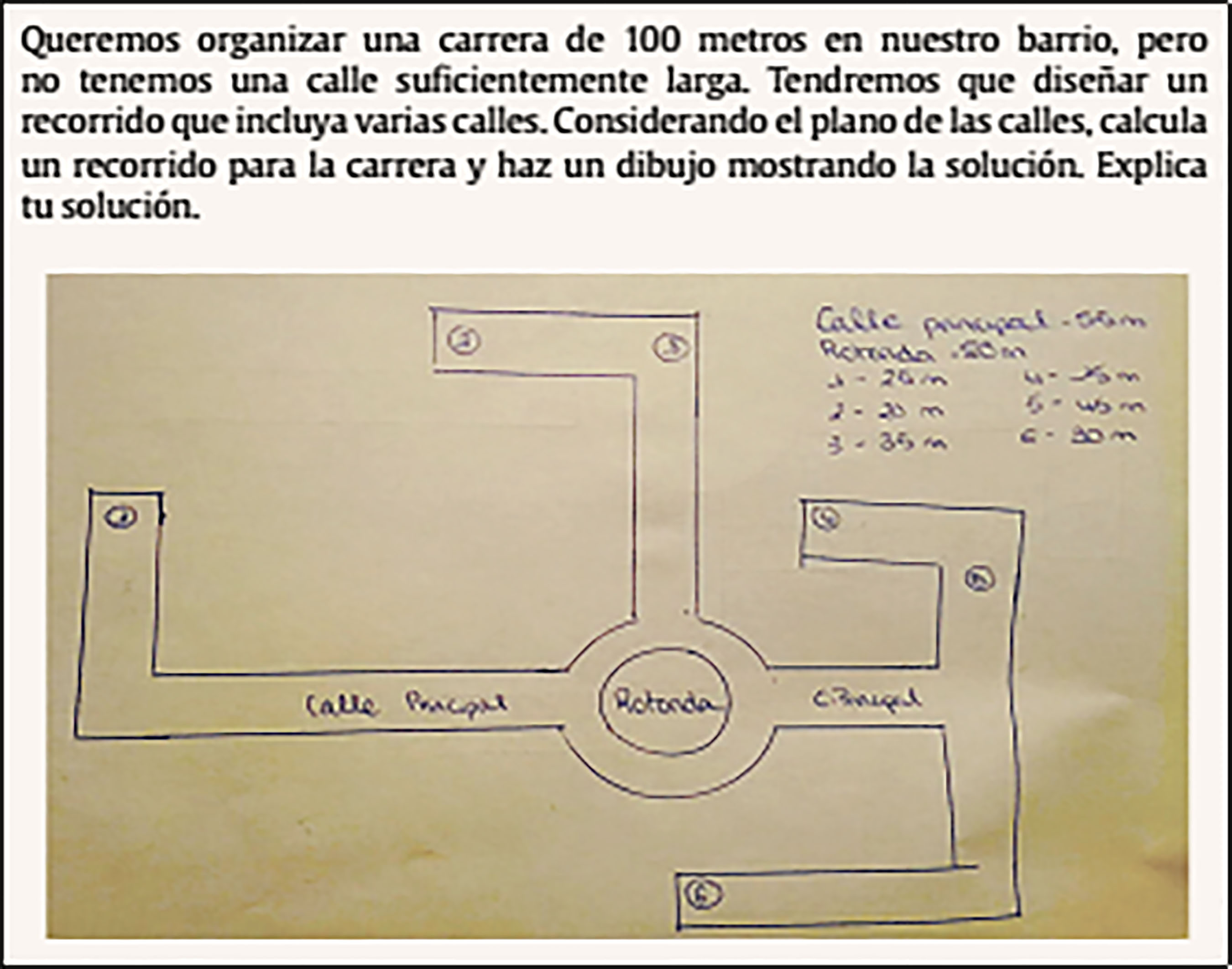 Figura 2 Solución sugerida con los pasos implementados sobre el mismo dibujo. 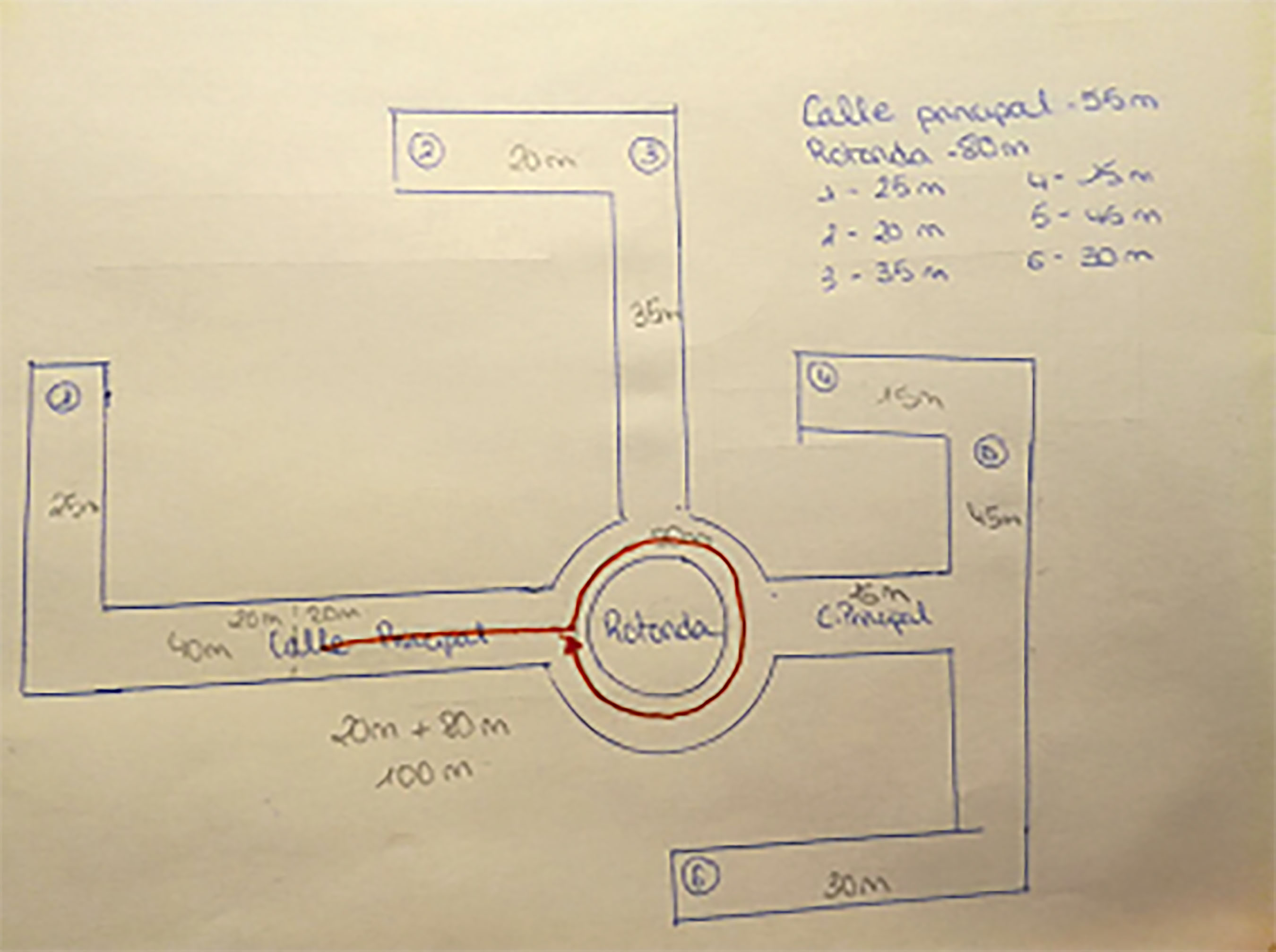 Las tres características menos importantes para los futuros maestros fueron contrastadas con las respuestas a Q2.3, coincidiendo que: a) la última, reflejaba que los datos debían ser claros (promedio 3.60), b) la penúltima reflejaba que el problema no podía solucionarse rápido (promedio 3.87) y c) la antepenúltima reflejaba que el problema debía representar un reto atractivo (promedio 5.13). Debajo se muestran dos respuestas a Q2.3 que muestran cómo estos tres aspectos no son importantes para ellos en los problemas de matemáticas: “Si tú eres muy listo, quizás puedas solucionarlo rápido, depende del problema. Creo que los datos son siempre fáciles de entender. No todos los problemas son interesantes, por eso no creo im portante que un problema represente un reto atractivo” (participante 3); “Si no eres bueno en matemáticas, quizás no existan problemas atractivos para ti y por eso serás lento resolviendo. Otra característica poco importante es que el enunciado debe usar datos claros, lo cual depende de los objetivos del problema” (participante 4). Los resultados muestran que las características consideradas más importantes no coinciden con las que mencionan más veces, como puede verse en la Tabla 5. Por ejemplo, la característica más mencionada, el uso de lenguaje simple y familiar, ocupaba la sexta posición de importancia para el grupo. También sucede con otras características de manera más pronunciada, como con las tres características siguientes: a) el uso de datos comprensibles, la cuarta más mencionada pero colocada en última posición por orden de importancia, b) los conceptos que se han trabajado en clase necesitan ser conectados para resolverlo, la 17ª más mencionada pero colocada en quinta posición de importancia y c) permite la creación de nuevos problemas a través de modificaciones, para practicar otros aspectos matemáticos, la novena más mencionada pero ordenada en la posición número según importancia. Tan sólo ha habido tres características en las que concuerda el orden de la frecuencia con que han sido mencionadas y el orden de importancia otorgado: la coherencia entre los datos y la pregunta (3ª posición), todos los datos necesarios se ofrecen en el enunciado (7ª posición) y es imposible la resolución en poco tiempo (penúltima posición). Relaciones entre el Problem-posing y el Problem-solving El segundo grupo de indicadores, “relaciones entre problem-posing y problem-solving” se ha creado para responder a este segundo objetivo de saber qué relaciones encuentran entre crear problemas y resolverlos. Engloba tanto una perspectiva conjunta como las ventajas de saber crear problemas. Los futuros maestros no presentan las diferencias entre crear problemas y resolverlos de manera clara y concisa. Numerosas respuestas a Q1.4 ilustran esta idea: el “problem-solving permite trabajar sobre la comprensión de los enunciados y el problem-posing permite mejorar el vocabulario matemático” (participante 5), “cuando hablamos de problem-solving pensamos en obtener una respuesta y cuando hablamos de problem-posing pensamos en el proceso que conduce a la respuesta” (participante 6) y “la creatividad e imaginación juegan un papel más importante en el problem-posing, mientras que en el problem-solving sólo interviene el conocimiento” (participante 7). Estas opiniones muestran una gran diversidad de pensamientos y poca concreción y nos induce a pensar que no conocen las diferencias. Lo que manifiestan tampoco es del todo correcto en ningún caso: el vocabulario no está claro que se pueda mejorar con la creación de problemas, cuando se habla de crear problemas también se debe pensar en obtener una respuesta y cuando se resuelve un problema también interviene la creatividad. Los futuros maestros consideraron que el problem-posing ayuda al problem-solving. Recordando el punto anterior, en el que se observa que no conocen las diferencias entre crear y solucionar problemas, la idea que consideren que crear problemas ayuda a resolverlos muestra que creen en un único proceso indivisible que consiste en crear y resolver conjuntamente o por lo menos les cuesta contemplar ambos procesos por separado. No tienen una idea clara de la manera en cómo ayuda. La siguiente respuesta a la pregunta Q1.5, que les pregunta de qué manera complementan las habilidades de crear problemas a las habilidades de resolverlos, ilustra esta idea: “para crear problemas, tienes que saber como resolverlos y saber resolver problemas es necesario para crearlos” (participante 8). Se les preguntó sobre la dificultad de crear y resolver problemas después de estudiar las opiniones de dos investigadores en didáctica de las matemáticas y después de que hubieran elaborado una lista ordenada de las características de los problemas. Respondieron a Q2.4 de la misma manera: crear problemas es más complicado que resolverlos; muchas opiniones lo manifiestan. Por ejemplo: “Crear problemas es más difícil porque hay muchas características a tener en cuenta. Cuando tú creas un problema, tienes que resolverlo también” (participante 9); “Para crear problemas, tienes que pensar en todas las características de un problema de la lista. Puede ser difícil incluirlas todas. Cuando resuelves un problema, tú sólo tienes que encontrar la estrategia correcta” (participante 10). Ambas respuestas reflejan que han aprendido que cuando se trata de crear problemas han de conseguir que éstos cumplan una serie de características, además de resolverlos. Así es que ahora han aprendido que la creación implica resolución. Los futuros maestros consideraron que saber crear problemas a la hora de enseñar matemáticas ofrece a los alumnos de primaria la oportunidad de profundizar en los conocimientos matemáticos enseñados, implicarse más en la resolución y estimular su autoconfianza. Estas ideas se muestran a continuación con respuestas a la pregunta Q1.2: “Se puede ayudar al estudiante a entender conceptos trabajados. Él hará que los estudiantes se sientan bien por considerar sus ideas importantes y ello ayuda a desarrollar el pensamiento matemático. También se les ofrece la oportunidad de descubrir sus errores y corregirlos” (participante 11); “Se podrá estimular la autoconfianza y así su implicación en la resolución” (participante 12). Estas ideas reflejan un reconocimiento de intencionalidad detrás de la creación de problemas, pues dicen que pueden profundizar en los conocimientos matemáticos enseñados. Otra opinión interesante desde la perspectiva de las ventajas de saber crear problemas para enseñar a resolver problemas mejorando las actitudes es: “Tenemos que luchar para una actitud positiva hacia la resolución de problemas. Tenemos que proponer situaciones en un contexto familiar al estudiante, y con un contenido adaptado” (participante 13). Esta opinión muestra el conocimiento de que saber crear problemas le permitirá adaptar mejor el contenido al alumno. Los futuros maestros no pueden señalar ventajas del problem-posing durante un curso de didáctica de las matemáticas. Las respuestas a Q1.3 fueron superficiales. Por ejemplo: “Ayuda a los futuros maestros a considerar un problema como una herramienta útil. Ellos aprenden a proponer problemas motivadores. Gracias a la interacción con la clase, aprenden diferentes soluciones, técnicas y perspectivas” (participante 14). Esta respuesta no es representativa de la mayoría de opiniones. Considerar el punto anterior, donde sí creían ventajoso el saber crear problemas cuando enseñan matemáticas a niños de primaria, induce a pensar que o bien piensan que ya saben crear problemas o bien no ven provechoso desarrollar o mejorar tal habilidad. Los futuros maestros consideraron que para crear un problema se debían dominar todos los conceptos y procesos requeridos para la resolución. La siguiente respuesta a la cuestión Q1.9, donde se pregunta cómo ayuda el problem-posing a evaluar, muestra esta idea: “Cuando creas un problema, sabes lo que estás preguntando, sabes los conocimientos previos usados. Sabes los estudiantes qué tienen que aprender y qué justificaciones tienen que usar. Estableces los objetivos y puedes ver si se han conseguido. También seleccionas el contenido que los estudiantes tienen que saber y evalúas los procesos” (participante 15). Habilidades del Problem-posing Los futuros maestros saben que necesitan estar al tanto de los conocimientos de sus futuros estudiantes para enlazarlos con las tareas que propongan. Algunas respuestas a la pregunta Q1.6 sobre los requisitos para crear problemas ilustran esta idea: “Tengo que dominar la materia. Tengo que ser creativo diseñando problemas originales. Tengo que tener una gran capacidad para pensar e investigar y debo anticiparme a las dificultades de aprendizaje que puedan aparecer” (participante 16); “Tengo que pensar claramente lo que quiero conseguir con el problema que cree, partiendo de los conocimientos de mis futuros estudiantes. Tengo que crear problemas atractivos con diferentes grados de dificultad” (participante 17); “Es necesario ser flexible y abierto de mente; son características trabajadas desde la creatividad. El grado de dificultad no puede sobrepasar a los estudiantes. Tenemos que estar al tanto de los conocimientos de los estudiantes y su nivel. Finalmente, tenemos que saber usar un lenguaje matemático adecuado y cómo preguntar cuestiones interesantes” (participante 18). Si recordamos que anteriormente no veían ventajas en practicar la creación de problemas en la Universidad, ello induce a reforzar el pensamiento de que se creen bien preparados en crear problemas, más que pensar que crear problemas no sea importante. Los futuros maestros consideraron como aspectos necesarios para crear problemas el grado de dificultad, un contexto familiar y objetivos claros. Las siguientes respuestas a Q1.7 lo reflejan: “Los problemas deben ser adecuados al nivel de los estudiantes, relacionados con sus intereses y en un contexto cercano a ellos. El objetivo debe ser claro” (participante 19); “Los aspectos son: material que pueda ayudarles, objetivos claros, saber el conocimiento previo de los alumnos” (participante 20); “Los aspectos son: los intereses de los estudiantes, el nivel de dificultad, el conocimiento previo y el nuevo conocimiento que el problema va a hacer referencia” (participante 21). Figura 3 Ejemplo de un problema y su modificación.  Después de estudiar las opiniones de investigadores en didáctica de las matemáticas y de la creación de problemas, todos los futuros maestros son conscientes de la necesidad de practicar más el problem-posing en cursos universitarios de didáctica de las matemáticas. Esta idea se observa en esta respuesta que plantea el hecho de un aprendizaje a partir de la creación de problemas en grupo en la universidad: “el problem-posing requiere mucha imaginación y, si prestas atención a los problemas creados por otros estudiantes, puedes aprender mucho” (participante 22). Los futuros maestros dijeron que necesitaban más práctica en el problem-posing, porque un problema es una herramienta útil para evaluar el conocimiento y el razonamiento. Las siguientes opiniones ejemplifican tal opinión: “Hemos practicado la resolución de problemas mucho, pero no su creación. Necesitamos más práctica” (participante 23); “Los futuros maestros tienen que saber cómo solucionar muchos problemas. Consecuentemente, ellos tienen que saber cómo crearlos. Así es que tienen que ofrecer una gran variedad de problemas, dependiendo del nivel de los estudiantes” (participante 24). Figura 4 Ejemplo de un problema con su solución. 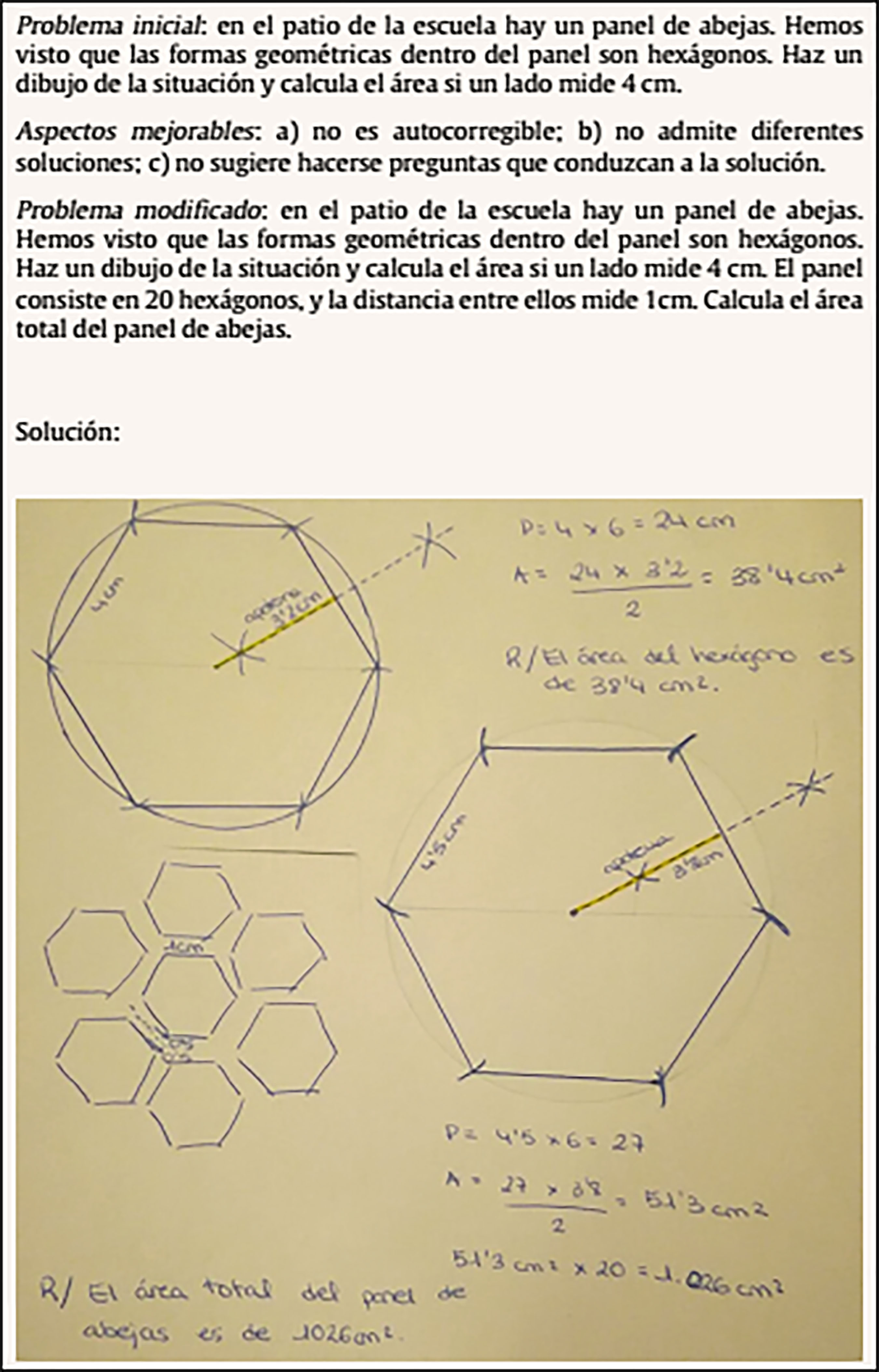 También, después de haber estudiado los dos artículos y de haber creado y revisado dos problemas, conocen el potencial que tiene crear problemas: para resolver dudas, para ayudar a comprender con ejemplos y para ejercitar objetivos, contenidos y procesos pensados con anterioridad. Esta opinión se refleja en las siguientes respuestas a Q2.5: “el problem-posing ayuda a saber qué quieres evaluar: hay más cosas que conceptos y contenidos trabajados; hay el proceso de razonamiento y reflexión. El creador del problema se guía por ciertos objetivos y contenidos que pretende que el estudiante practique” (participante 25); “Los problemas responden muchas dudas. Son como ejemplos y pueden ayudar a comprender” (participante 26). Todos los futuros maestros cambiaron sus problemas originales para mejorarlos. Las diferentes razones fueron: a) eran demasiado fáciles y poco útiles, b) no admitían diferentes vías de solución, c) no sugerían nuevas cuestiones induciendo a la solución, d) los enunciados no incluían ilustraciones que podían ayudar a comprender, e) no podían ser autocorregibles y f) podían ser más atractivos usando un lenguaje más familiar y un contexto más cercano a la vida cotidiana, incluyendo un trabajo experimental. Múltiples respuestas a Q2.1 ejemplifican estas ideas. Por ejemplo, la siguiente respuesta dada por el participante 27 (Figura 3) muestra que las modificaciones se han ejecutado porque el enunciado debería ser más claro e incluir una representación, carece de utilidad y su enunciado debería ser más cercano a la vida cotidiana del estudiante. Otro ejemplo, la respuesta dada por el participante 28 (Figura 4), muestra que las modificaciones se han ejecutado porque el problema debería ser autocorregible, debería admitir diferentes resoluciones, debería sugerir nuevas cuestiones induciendo a la solución y el enunciado debería ser más claro e incluir una representación. Un Mecanismo Didáctico para Mostrar a los Futuros Maestros la Utilidad del Problem-posing cuando se Enseña a Resolver Problemas Después de haber leído los dos artículos propuestos y haber creado y revisado sus dos problemas, los futuros maestros pensaron que era necesario estudiar cómo crear problemas en la universidad. Todos estos pasos constituyen un mecanismo didáctico que hace reflexionar sobre las oportunidades que ofrece crear problemas a la hora de enseñar a resolver problemas. Además, nos ha servido para recoger diversas opiniones. Ellos tienen opiniones diferentes, como reflejan las respuestas a Q2.5. Por ejemplo, una opinión compartida por varios futuros maestros fue la no dependencia de los libros de texto: “Un buen maestro debería ser capaz rápidamente de proponer tareas para aclarar cualquier duda y no mirar siempre el libro de texto. Saber cómo crear problemas ayuda a modificar la dificultad de un problema de un libro si algún estudiante lo necesita” (participante 29). Otra opinión fue que sabían cómo resolver problemas, pero no cómo crearlos. Esta idea se refleja en las siguientes respuestas: “Nosotros sabemos cómo resolver problemas. La cosa es que no sabemos cómo crearlos. En el futuro, sería útil ser capaz de crear problemas y no depender de los libros de texto” (participante 30); “Es muy importante porque, como estudiantes, los futuros maestros hemos practicado resolver problemas, pero como maestros no hemos practicado las habilidades de crearlos” (participante 31). Otra opinión interesante fue que los maestros pueden usar el problem-posing para resolver dudas: “Así lo creo pues en el futuro, tendremos que crear más problemas de los que vamos a resolver. Es interesante aprender diferentes estrategias para resolver problemas, pero es más interesante aprender cómo crear problemas. Los problemas resuelven muchas dudas, porque son como ejemplos y ayudan a comprender” (participante 32). Discusión y ConclusionesDado que en matemáticas es esencial enseñar a resolver problemas (Santaló, 1994), es necesario que los docentes dediquen tiempo y recursos a desarrollar las habilidades de resolución de problemas de sus estudiantes. El profesor debiera prestar atención especial a las 4 fases de Polya de resolución de problemas (Polya, 1970): 1) comprensión del enunciado, 2) diseño de una estrategia resolutiva, 3) ejecución de la estrategia y 4) revisión. La creación de problemas con intenciones educativas ayuda a los docentes de matemáticas en este aspecto (Mallart et al., 2016). Si los futuros maestros quieren sacar el máximo partido a este recurso en el aula para enseñar a resolver problemas, tendrán que estudiar y practicar el problem-posing. Este estudio se planteó bajo la hipótesis de que en la enseñanza preuniversitaria no se trabaja suficiente la creación de problemas de matemáticas, ocasionando que los futuros maestros no consideren el problem-posing una herramienta útil para enseñar a resolver problemas. Para contrastar esta hipótesis, se consideraron básicamente tres objetivos específicos y se introdujo un mecanismo didáctico para mostrar la utilidad de crear problemas para enseñar a resolverlos. A continuación, se expondrán las conclusiones que se extraen sobre cada objetivo y luego se extraerán conclusiones conjuntas para acabar aceptando la hipótesis de trabajo. El primer objetivo de esta investigación fue estudiar las características de un problema para los futuros maestros. El grupo consideró que la característica más importante era que la dificultad del problema fuera la adecuada para el conocimiento del alumno. La segunda característica más importante era la utilidad de su solución. Otra característica importante era la implicación en la resolución de conceptos trabajados. Otra característica dice que la comprensión de conceptos anteriores se hace más fácil. El análisis de la importancia dada a estas tres características reveló un interés en la resolución de problemas porque pensaban que era útil para enseñar matemáticas. Ellos no consideran importante la característica de que diferentes caminos pueden dirigir a la misma respuesta. Ellos no consideran que sea esencial para un problema representar un reto atractivo. Estas dos ideas exponen que no disfrutan resolviendo problemas. Por otro lado, si analizamos por qué las características más mencionadas no son las que se clasifican como las más importantes, se ve que cuando elaboran la clasificación han aprendido nuevas características que les parecen más importantes. De este modo se concluye que existe un desconocimiento de las características más importantes de los problemas. El segundo objetivo de esta investigación fue establecer las relaciones entre la resolución de problemas y su creación, según los futuros maestros. Los resultados muestran que no tienen claro sus diferencias, les cuesta contemplar ambos procesos por separado. El hecho de que no tengan claro qué es más difícil, si crear problemas o resolverlos, muestra que no tienen claras las propiedades de cada proceso. Esto refleja que en los estudios preuniversitarios se ha trabajado poco la creación de problemas. Saber crear problemas cuando se enseñan matemáticas a alumnos de primaria dicen que les permite ofrecer a los alumnos profundizar en las matemáticas enseñadas, implicarlos más en la resolución de problemas, estimular su autoconfianza y adaptar mejor el contenido al alumno. De este hecho, y de que no vean ventajas en practicar crear problemas en un curso universitario de didáctica de las matemáticas, se concluye o bien que consideran que ya saben crear problemas o bien que no resulta provechoso desarrollar o mejorar su habilidad en crear problemas. En cualquiera de estos dos casos es necesario enseñar a los futuros maestros que el problem-posing ayuda a estimular la creatividad y especificar la situación, el lenguaje, los conceptos, las proposiciones, los procesos y las explicaciones (Malaspina, 2011). El tercer objetivo de la investigación fue conocer las habilidades de los futuros maestros del problem-posing. Ellos piensan que para crear problemas necesitan saber los conocimientos previos de sus estudiantes. English (2003) insiste en que los maestros deben ajustar su proceso de enseñanza al nivel real de sus estudiantes. Los futuros maestros tienen que saber cómo proponer un problema con un grado de dificultad adecuado. Esta investigación muestra que los futuros maestros están de acuerdo con que: a) el problema debe presentar una dificultad adecuada a los conocimientos de los estudiantes, b) el contexto tiene que ser cercano a la vida cotidiana de los estudiantes y c) el objetivo del problema tiene que ser claro. Después de trabajar en clase la creación de problemas, los futuros maestros reconocen que les falta práctica. Esto también fue observado por Ellerton (2013). Esta investigación muestra que los futuros maestros piensan que deberían estudiar la creación de problemas en la universidad. Este reconocimiento, después de introducir el mecanismo didáctico para mostrar que el crear problemas, es útil para que ellos enseñen a resolver problemas y refuerza la idea de que se creían bien preparados en crear problemas. De hecho, todos modifican sus problemas porque no sabían cómo crear problemas. Todos los aspectos que señalaron estar de acuerdo sobre lo que debía cumplir un problema no fueron capaces de seguirlos en sus propios problemas creados por falta de habilidades en creación de problemas. Los motivos que subrayan que ocasionaron sus modificaciones fueron: a) demasiado fáciles o difíciles y con una resolución poco útil y atractiva, b) no posibilitar diferentes soluciones, c) no sugerir nuevas cuestiones interesantes que pueden guiar hacia la respuesta, d) falta de claridad en el enunciado (fácilmente mejorable con un dibujo), e) dificultad en la autocorrección (un trabajo experimental ayudaría) y f) enunciados no próximos a la realidad del alumno. Esto refuerza la hipótesis de trabajo de que no se trabaja suficiente la creación de problemas en los estudios preuniversitarios. También en esta investigación se introdujo un mecanismo didáctico con la voluntad de mostrar a los futuros maestros la utilidad de la creación de problemas para enseñar a resolverlos. Cumpliendo con las tareas propuestas (creando dos problemas, resolviéndolos, leyendo las opiniones de dos investigadores en didáctica, revisando y mejorando los dos problemas), los futuros maestros estudiaron las oportunidades ofrecidas por la creación de problemas desde el punto de vista de la enseñanza de la resolución de problemas. Por ejemplo, observaron que no dependían de los libros de texto y que podían usar la creación de problemas para aclarar dudas proponiendo ejemplos adecuados. Se dieron cuenta que la creación de problemas tenía más usos que evaluar el grado de comprensión. Un buen docente de resolución de problemas debe conocer el máximo número de herramientas y técnicas para abordar su propósito y la creación de problemas constituye una herramienta muy poderosa (Leung y Silver, 1997; Pino-Fan y Godino, 2015). En esta investigación, y en un estudio de Tichá y Hošpesová (2013), los futuros maestros crean problemas, los modifican y evalúan los procedimientos para resolverlos. Juntando las conclusiones principales de los objetivos propuestos se puede dar respuesta al objetivo general de conocer lo que piensan los futuros maestros sobre saber crear problemas para enseñar mejor a resolver problemas, tras una pobre práctica preuniversitaria en crear problemas. El estudio del primer objetivo nos muestra que hay un desconocimiento extendido de las características importantes de un problema. El estudio del segundo objetivo nos muestra que conciben el crear problemas y el resolverlos como una misma tarea. El estudio del tercer objetivo nos muestra que creen estar bien preparados para crear problemas, pero el mecanismo didáctico introducido concluye que no saben crear problemas. De esta manera se concluye que difícilmente pueden concebir el crear problemas como una herramienta útil para enseñar a resolver problemas si no saben las características de los problemas, ni tampoco los saben crear persiguiendo unos objetivos claros, ni lo consideran una tarea diferente a la de resolver problemas. Si no saben crear problemas con intenciones educativas predeterminadas, no ven ninguna relación entre el crear problemas y enseñar matemáticas; tampoco en enseñar a resolver problemas porque no buscan que el resolutor ejercite nada en concreto. Las conclusiones de este estudio conducen a aceptar la hipótesis de trabajo de la falta de trabajo preuniversitario en materia de creación de problemas. Esta investigación está en la línea de los trabajos de Pelczer y Gamboa (2008) y de Singer et al. (2011), cuando exponen que muchos maestros no han desarrollado habilidades en crear problemas y también en la línea de Ellerton (2013), cuando afirma que los futuros maestros reconocen la necesidad de trabajar más la creación de problemas. Extended Summary Multiple authors show a strong relation between problem-solving and problem-posing. Silver and Cai (1996) show that problem-solving success is closely correlated with success in posing problems. English (1997) established that to be able to create a problem, a framework of knowledge is needed, and it is necessary to understand what is a problem, recognize its structures and characteristics, and identify similar structures. Kesan, Kaya, and Güvercin (2010) studied the influence of problem-posing on the development of mathematics skills. Espinoza, Lupiáñez, and Segovia (2014) studied talented students and showed that the problems created by talented students contained longer statements and interrogative propositions, and that the number of processes and steps involved in the solution of the problems was greater than in problems created by the standard group. The aim of this research was to find out if pre-service teachers consider important to be able to create problems to teach problem-solving. In order to answer this question, we formulated three specific sub-objectives related to pre-service teachers: a) to find out the characteristics of a problem, b) to find out the relations between problem-posing and problem-solving, and c) to find out which problem-posing skills they have developed. In addition, we introduced an educational mechanism to show pre-service teachers the usefulness of problem posing in teaching problem-solving. These sub-objectives were established to accept or reject the working hypothesis. In pre-university mathematics education there is no practice enough in creating problems. We have considered Ellerton’s research (2013), in which pre-service teachers recognize the importance of problem-posing, but they acknowledge that they have had few opportunities to practise it. We have considered also research by Pelczer and Gamboa (2008) and Singer, Ellerton, Cai, and Leung (2011) in which many teachers do not seem to have developed problem-posing skills. The sample consisted of 94 pre-service mathematics teachers who were studying a geometry education course at the public University of Barcelona. Many instruments of written records were used to pick up different kinds of information: questionnaires, classroom observations, sequences of tasks, and registers in the moodle. Results were analyzed from the perspective of three sets of indicators: a) indicators referring to the features of problems, b) indicators referring to the relationship between problem-posing and problem-solving, and c) indicators referring to the problem-posing skills. We designed four tasks: a) answering a questionnaire with ten open questions asking for characteristics of the mathematics problems, differences between problem-solving and problem-posing, requirements needed to be able to pose problems, relations between problem-posing and testing, and a creation and their solution of two geometry problems for the last course of primary school, where at least one triangle and another mathematical figure appeared; b) giving pre-service teachers an article about how to teach and learn mathematics from problems (Xavier de Mello, 2000) and an article about the meaning of a suitable problem in the context of a teacher’s training; c) answering a questionnaire with five open questions asking for reviewing their two problems created before and proposing modifications if it was necessary with a justification and with the new solution; and d) elaborating an ordered list following the importance they give to all characteristics considered in the second previous article. Research question can be answered from sub-objectives conclusions. Analyzing each sub-objective, we can find out what pre-service teachers think about creating problems to teach problem-solving. The study of the first sub-objective shows that pre-service teachers do not know the most important characteristics of a mathematics problem. The group considered the most important characteristics: a) “the difficulty of the problems matches the students’ knowledge”, b) the problem’s usefulness when solved, and c) concepts that have already been worked on need to be connected to solve the problem. They do not identify the most relevant characteristics as the most mentioned. We can assume that while they are doing the classification, they are learning new characteristics that are more relevant for them. The study of the second sub-objective shows that pre-service teachers consider problem-posing and problem-solving as the same task. They do not think that practicing problem-posing at university offers them any advantage. We can assume that pre-service teachers think they already know how to create problems with educational intention or they think that developing or improving their posing-problems skill is not interesting enough. They need to be taught that problem-posing helps to stimulate creativity and specify the situation, the language, the concepts, the propositions, the processes, and the explanations (Malaspina, 2011). The study of the third sub-objective shows that pre-service teachers say that they are well prepared to create problems with educational intention. But after the educational mechanism was introduced to show pre-service teachers the usefulness of problem-posing in teaching problem-solving, we conclude that they do not know how to create problems with educational intention. Pre-service teachers agree that: a) the problem has to present a level of difficulty that is in line with students’ knowledge, b) the context has to be relevant to their daily life, and c) the problem’s goal has to be clear. After the educational mechanism was introduced, this research shows pre-service teachers think they should study problem-posing at university. This was also observed by Ellerton (2013). All of them changed their problems because: a) the problems were too easy or too difficult and their solution was useless and not interesting, b) the problems did not accept different ways to be solved, c) the problems did not suggest new interesting questions, d) the problems did not have clear statements (easily improvable with a picture), e) the problems were difficult to be self-corrected (an experimental work could help), and f) the problem statements were not close enough to the students’ daily life. All of these points let us accept the working hypothesis – there is not enough practice in problem-posing in pre-university studies –, so they are not interested in problem-posing. In conclusion, pre-service teachers do not consider problem-posing as a useful and efficient tool to teach problem-solving. They do not know the main characteristics of a problem and they do not know how to create problems following clear objectives. They do not consider problem-posing and problem-solving two different tasks. Para citar este artículo: Mallart-Solaz, A. (2018). Interés de los futuros maestros en saber crear problemas de matemáticas para enseñar a resolverlos. Psicología Educativa, 25, 31-41. https://doi.org/10.5093/psed2018a17 |
Para citar este artículo: Mallart-Solaz, A. (2018). Interés de los futuros maestros en saber crear problemas de matemáticas para enseñar a resolverlos. Revista Psicología Educativa, 25, 31-41. https://doi.org/10.5093/psed2018a17
Correspondencia: alberto.mallart@gmail.com (A. Mallart Solaz).
Copyright © 2026. Colegio Oficial de la Psicología de Madrid








 e-PUB
e-PUB CrossRef
CrossRef JATS
JATS








