Teaching Quality: An Explanatory Model of Learning in Secondary Education

Introduction

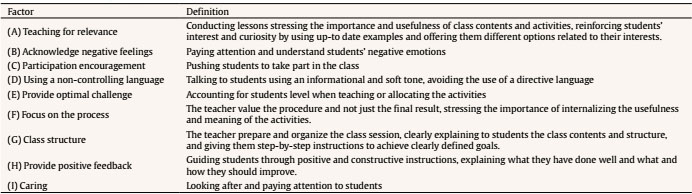
Identifying teaching-related behaviors that prevail on students’ optimal functioning has been a relevant research topic in recent years (Stroet et al., 2015a; Trautwein et al., 2015). Improving students’ learning is a widespread educational concern, and previous literature has shown that teaching quality plays a key role enhancing students’ learning and outcomes (Wallace et al., 2016). In this regard, previous studies have consistently shown shown what teachers do in the classroom meaningfully influence students’ learning, and that having effective teachers eases students to reach their full potential (Maulana et al., 2015; Torrijos et al., 2018).

However, there is a lack of sufficient literature regarding the specific behaviors of math teachers that impact on students’ performance (Rimm-Kaufman et al., 2014). This deserves special attention for secondary education, since math abilities play a direct role in students’ competences to be successful in school (Gaspard, 2015; Kosovich et al., 2015) and affect students’ future academic and professional performance (Seaton et al., 2014). Moreover, at secondary education stage, students’ interest in school usually lessens, and their math achievement gets significantly worse (Kiemer et al., 2015). This highlights the necessity of better knowing how secondary math teachers can enhance their students’ learning. Furthermore, understanding the educational climate that promotes students’ optimal outcomes is especially important in contexts where students usually have low expectancies for success and low value for engaging in the subject (Getty et al., 2017).

In order to extend the knowledge about how teachers’ behaviors affect students’ learning in a domain such as math, in this study we purposed to explore the relationships between teaching quality and other students’ achievement-related variables. Thus, we tested a model to search for associations between teaching quality and students’ task-expectancy, task-value, effort regulation, connection frequency, and future interest. Four aims guided the conduct of the study: (1) to test if teaching quality predicts, at class level, students’ task-expectancy; (2) to assess if teaching quality predicts, at class level, students’ task-value; (3) to test if students’ task expectancy predicts, at individual and class levels, students’ connection frequency, effort regulation, and future interest in math; and (4) to assess if students’ task-value predicts, at individual and class levels, students’ connection frequency, effort regulation, and future interest.

Teaching Quality

Teaching quality alludes to teacher-student interactions in the classroom (Cornelius-White, 2007), and it is especially referred to teachers’ behaviors that enhance positive educational outcomes in students (Cochran-Smith & Fries, 2005). Although it is an increasingly researched topic, there appeared to be a lot of conceptual confusion concerning it, and different terms have been used interchangeably to represent the same idea (see Day et al., 2015; Kunter et al., 2013; Rjosk et al., 2014). Despite this conceptual confusion, unfortunately very common in our discipline (Murphy & Alexander, 2000), researchers widely agree that students’ learning and outcomes are strongly related with the quality of classroom processes (Inda-Caro et al., 2019; Maulana et al., 2015).

Within Self-Determination Theory (SDT; Deci & Ryan, 1985, 2017), a positive teaching quality refers to teachers’ behaviors that support students’ needs for autonomy, competence, and relatedness. More specifically, autonomy refers to the feeling of performing an activity without external pressures, students feeling that school actions emanate from their self and that academic activities are consistent with their own interests (León et al., 2017; Wang & Eccles, 2013). Competence refers to the sense of interacting effectively with the environment, and to the students’ belief of successfully achieve at school activities and learning tasks (León et al., 2017; Ng et al., 2011). Lastly, relatedness alludes to the need to build and maintain positive and meaningful relationships. Precisely, when students sense that their feelings receive attention and they feel special and important for their teachers, they usually feel closer and related with them (Reeve, 2006; Stroet et al., 2013). In this sense, guided by SDT, several authors have explored teaching quality dimensions and teachers’ behaviors that support those students’ needs. In detail, to foster students autonomy, different authors have highlighted many strategies such as providing students meaningful and explanatory rationales (Guay et al., 2013; Stroet et al., 2013), nurturing students’ inner motivational resources (Cheon & Reeve, 2015; Reeve et al., 2014; Stroet et al., 2013), offering them meaningful choices (Núñez et al., 2012; Vansteenkiste & Ryan, 2013), acknowledging students’ negative feelings (Su & Reeve, 2010; Taylor & Ntoumanis, 2007; Vansteenkiste et al., 2012), encouraging their participation in class (Gillet et al., 2012; Roth et al., 2007), and using a non-controlling language (Hagger et al., 2015; Simons et al., 2005). On the other hand, to promote students’ competence, different authors have recommended teachers to provide an optimal challenge (Cheon & Reeve, 2015), to focus on the process (Kusurkar et al., 2011; Tessier et al., 2010), to provide a positive and specific feedback (Hattie & Timperley, 2007; Hospel & Galand, 2016; Thurlings et al., 2013), and to prepare and structure the lessons (Hospel & Galand, 2016; Vansteenkiste et al., 2012). Finally, to foster students’ need for relatedness, Stroet et al. (2013) have suggested teachers to pay attention to students’ feelings and to show them interest and trust.

Based upon this previous literature, from which different authors have focused separately on specific items to support students’ autonomy, competence, or relatedness, León et al. (2017) developed a global approach under the label teaching quality. The authors developed and validated a scale to assess students’ perceptions of those specific teachers’ behaviors during class, grouped in nine factors under the label teaching quality. These factors, shown in Table 1, allow capturing specific and well-defined teachers’ behaviors that are amenable to intervention and improvement (León et al., 2017).

Although previous research following SDT tenets has widely explored the relationship between teaching quality and students’ motivational constructs, most of them have focused just on few items that support students’ autonomy, competence or relatedness, but not on a teaching quality global approach. Likewise, although some studies have addressed the concept of teaching quality in relation to Eccles’ (1983, 2009) expectancy-value theory, they have also used different and isolated indicators of teaching quality (e.g., Becker et al., 2014), they have barely focused on students’ enhancement of task value (e.g., Hulleman & Harackiewicz, 2009), or they have not been carried out taking into account the nested nature of their data (e.g., Lazarides et al., 2019). In this regard, most of the research that has slightly addressed teachers’ behaviors based on Eccles’ theory has develop interventions designed to increase students’ perceptions of the relevance of school contents, but to the best of our knowledge never before have the other indicators of teaching quality been linked with students’ expectancies and values. As already noted, research on this topic is scarce, so efforts to better explore how math teachers’ behaviors in classroom can enhance their students’ motivation are still warranted.

On Students’ Expectancy-Value Motivation

Expectancy-value theory (Eccles, 1983, 2009) is one of the most influential frameworks for understanding student motivation and how it affects choices and achievement in academic settings (Bergey et al., 2018; Gaspard et al., 2019). This model suggests that students’ choices, persistence, and academic performance can be explained by their beliefs about their capacities to successfully perform a task, as well as by the extent to which they subjectively value the activity in hand (Eccles, 1983, 2009). Thus, the more capable students perceive themselves, expect to be successful and value the task, the more likely they are to choose to engage and persist in the activity, and also to achieve better outcomes (Bergey et al., 2018).

Within their model, Eccles and colleagues specifically define “expectancy beliefs” as the conviction that one can succeed at task or activity, and “task value” as the perceived value that the individual has about the task in hand or the extent to which they think the activity is worthwhile (Kosovich et al., 2015). They distinguish between several dimensions into both expectancy beliefs and task values. Expectancy beliefs theoretically include two dimensions: “ability beliefs”, which refers to students’ beliefs of what they can do now, and “expectancy beliefs”, which refers to the students’ beliefs about what they think they can do in the future. However, these differences are founded on the theory, since empirically these dimensions have often been highly correlated and it is common to use both constructs interchangeably (e.g., Wigfield & Eccles, 2000). On the other hand, task value includes three dimensions, regarding what intensifies or diminishes the student’s value for the task: “intrinsic value” (the student values the activity because they perceive it as inherently enjoyable), “attainment value” (the student values the activity because of the perceived personal importance for certain aspects of the students’ identity such as the self-concept, self-worth, and identity), and “utility value” (the student values the activity because of the perceived usefulness or relevance for other tasks or aspects of their life).

In this paper, we focused on students’ expectancy beliefs and subjective task-utility value, as these constructs have been usually related with other achievement behaviors (Eccles, 1983; Lazarides et al., 2019). In line with previous studies that have found connections between these variables (e.g., Durik et al., 2015; Getty et al., 2017; Hulleman et al., 2017; Wigfield & Eccles, 2000), we consider them as potential variables to promote students’ connection frequency, future interest, and effort in math.

On Students’ Connection Frequency

Students’ connection frequency refers to how students find connection between different learning situations, and it is a mechanism for utility value intervention effects (Hulleman et al., 2017). Previous research has linked connection frequency with students’ expectancy beliefs and their perceived value of a task (Hulleman et al., 2017). According to Hulleman et al. (2017), these connections lead students to easily adapt a skill from one situation to another, to make associations between an activity and their lives, to comprehend the new material from a different perspective, to deeply process the information they receive and, as a result, to improve their learning. Regarding math, for example, a student may find stimulating to connect percentages to the need of calculating the discounted prices on sales, to understand the number of ingredients in a product or to calculate a basketball player’s free throw percentage. Stimulating students to make their own connections between the class contents and other aspects closer to their interests is especially beneficial for students with low performance expectations (Hulleman et al., 2010).

Despite the significance of assessing connections in the educational context and the importance of making efforts to help students to make their own associations (Hulleman & Harackiewicz, 2009), connection frequency is a recently developed construct and too little research has empirically focused on this topic. Thus, although previous literature has addressed similar constructs, such as critical thinking, attention strategies or deep strategy to learn (see Biggs & Tang, 2007; Cano-Garcia et al., 2014; Tejedor-Tejedor et al., 2008), to the best of our knowledge only two studies (Hulleman et al., 2010; Hulleman et al., 2017) have particularly tested students’ connection frequency. In this regard, Hulleman et al. (2010) and Hulleman et al. (2017) tested connection frequency as a mechanism for utility value interventions with undergraduate students, both highlighting that students’ connection frequency was a meditational variable and a key factor through which these interventions impacted academic outcomes.

Despite this lack of literature, it is a priority issue for education in the 21^st century to encourage students to apply school contents in their lives, to relate what they know to the contents they are learning, and to deeply process information they receive (Kong, 2014; Yang, 2012). This study aims to contribute to the literature trying to better understand how teachers can enhance these connections through teaching quality.

On Students’ Future Interest

Interest in a domain is defined as “the psychological state of engaging or the predisposition to reengage with particular classes of objects, events, or ideas over time,” and it has been identified as a significant condition for learning (Hidi & Renninger, 2006, p. 112). Interest is promoted by perceived value and developing knowledge in it (Getty et al., 2017; Kosovich et al., 2015), and a way to enhance it is to find value and meaning in activities in hand (Hidi & Renninger, 2006). According to Hidi and Renninger (2006), there are two types of interest: “situational and individual interest”. The former refers to “the focused attention and the affective reaction that is triggered at the moment by environmental stimuli, which may or may not last over time” (Hidi & Renninger, 2006, p. 113). In other words, it is the interest a student experiences in response to situational cues when engaging in a task (Harackiewicz et al., 2008; Hidi & Renninger, 2006). The second, individual interest, is defined as a “person’s relatively enduring predisposition to reengage particular content over time as well as to the immediate psychological state when this predisposition is activated” (Hidi & Renninger, 2006, p. 113). Hence, it refers to the initial and deeper interest students could display toward a topic, probably because they have had previous experiences relating it (Harackiewicz et al., 2008). Interestingly, the individual interest does not completely determine the interest toward a particular learning situation (Durik et al., 2015), so students without an initial individual interest toward math could develop a situational interest toward a specific learning situation. Moreover, according to Hidi and Renninger (2006)’s model of interest development, if learners find tasks or school contents meaningful and involving, this situational interest could last longer and, over time, could develop into individual interest. This approach is especially important for educators and researchers, since it means that students’ interest in math is amenable to be improved.

Drawing on the expectancy-value theory, several authors have shown that students’ expectancies and values are related to their interest toward a subject (e.g. Harackiewicz et al., 2008; Hulleman & Harackiewicz, 2009; Kosovich et al., 2017; Rozek et al., 2017). Most of the research on this topic, especially regarding STEM subjects, have focused on interventions designed to promote interest through the manipulation of students’ task-expectancies and values (see Durik et al., 2015; Harackiewicz et al., 2016; Hulleman et al., 2016; Nagengast et al., 2018, for a review). These interventions, conducted to increase students’ beliefs about the value of the content they are learning, have shown that situations that highlight tasks values promote the development of situational interest, which, in turn, can develop across situations and become into individual interest (Hulleman et al., 2010). In consequence, although teachers cannot directly influence students’ initial individual interest, it is a variable amenable to be modified through the perception of expectancy-value and students’ experience of situational interest.

A large body of literature has shown that interest has relevant benefits in the educational context. Interest affects, among others, students’ effective learning (Hulleman et al., 2010), performance (e.g., Harackiewicz et al., 2008; Hulleman et al., 2010; Hulleman & Harackiewicz, 2009), educational choices and decisions (Harackiewicz et al., 2002; Pike & Dunne, 2011), self-efficacy (Lipstein & Renninger, 2007), attention, and engagement (Harackiewicz et al., 2016). Moreover, it is a doubly important outcome to take into account if we consider that students’ interest during secondary education significantly decreases, and that their math achievement usually gets worse (Kiemer et al., 2015; Stroet et al., 2015b).

Effort Regulation

Students’ expectancy and value are also related to other motivational constructs such as effort regulation (Dietrich et al., 2015; Eccles, 2005; Kusurkar et al., 2013; Lazarides et al., 2019). According to Eccles’ (1983, 2009) theory, expectancy and task value are promoters of investing effort into learning (Dietrich et al., 2017), which is, in turn, considered as a strong predictor of academic achievement (León et al., 2015). Although there are different theoretical frameworks to address the concept of effort, such as the volitional framework (Corno, 2004) or the temperament perspective (Rothbart et al., 2003), in this study we tested effort from a self-regulated learning perspective (Zimmerman, 2013). From this perspective, effort regulation is defined as students’ process to appropriately manage their behavior to achieve their learning goals (Zimmerman & Kitsantas, 2014). In other words, effort regulation can be understood as students’ perceived investment – in time, work and energy – dedicated to a task or activity (Liew et al., 2011), and also as students’ ability to exert effort and persist even when doing it is not fun or easy (Pintrich & de Groot, 1990).

In the educational context, specifically in math, several studies have demonstrated the linkages between students’ effort and expectancy-value motivation, commonly showing that students’ with lower levels of motivation reported lower levels of effort, and students characterized by high levels of motivation (task value or expectancy beliefs), also displayed higher levels of effort regulation (see Dietrich et al., 2015; Dietrich et al., 2017; Kusurkar et al., 2013; Lazarides et al., 2019, for review).

Educating students to become self-regulated learners is one of the priorities for modern education (Yang, 2012), and a large body of literature has widely shown that effort regulation is a key predictor in enhancing students educational outcomes (León et al., 2015), Therefore, it seems important to better understand the factors that support students’ effort in math and how teachers can enhance it.

The Present Study

To date, no studies have analyzed the association between teaching quality and students task expectancy, task value, connection frequency, interest, and effort-regulation. In this study, we aim to explore the associations between these variables within the secondary education context, specifically in math.

The following research questions were addressed to examine whether: (Research Question 1) teaching quality predicts, at class level, students’ task expectancy; (Research Question 2) teaching quality predicts, at class level, students’ task-value; (Research Question 3) students’ task expectancy predicts, at individual and class levels, students’ connection frequency, effort regulation, and future interest; and (Research Question 4), students’ task-value predicts, at individual and class level, students’ connection frequency, effort regulation and future interest.

Regarding our first research question, we hypothesize, according to previous literature (Becker et al., 2014; Lazarides et al., 2019; Wang, 2012), that teaching quality will predict students’ expectancy and task value. Concerning our second, third, and fourth research question, we hypothesize that students’ expectancy and value motivation will be positively related to students’ connection, interest, and effort in math. This is consistent with previous studies which stated that expectancy-value motivation predicts students’ connection frequency (Hulleman et al., 2017), interest (Durik et al., 2015; Getty et al., 2017), and effort (Dietrich et al., 2017; Kusurkar et al., 2013; Lazarides et al., 2019). Besides, these hypotheses were addressed considering the nested nature of the data, which allowed us to obtain more information about the variables tested (Morin et al., 2014). In sum, the following multilevel model was proposed (see Figure 1).

Method

Participants

We recruited 1,113 students (510 females, 488 males, 15 not specified) from 55 classes of eight high schools in Gran Canaria, Spain. Students were from second to fourth grades of secondary education (8^th to 10^th grades in the US system), and their mean age was 15.28 (SD = 1.11). The average number of participants in each classroom was 20.236. School size was around 700 students. Participation was strictly voluntary, and all participants were informed of the data confidentially.

Procedure

This study was conducted at eight high schools located in Gran Canaria, Spain. First, we contacted high schools by phone to briefly explain the study. Once we obtained permission from the high school heads, we requested an appointment with math teachers of agreeing centers to explain the study in detail and request their cooperation. Mathematics teachers, school principals, and parents authorized participation in the study. Surveys were administered during the second semester. They were conducted in students’ mathematics classrooms, each researcher personally administered questionnaires, and it took about 20 minutes for students to complete them. Math teachers were invited to wait outside the classrooms during surveys administration. Participants were informed of the confidentiality of the data and the need for accuracy in responses.

Measures

Participants completed a questionnaire with demographic questions and measures of task-expectancy motivation, task-value motivation, connection frequency, effort-regulation, and future interest in math. They also completed questions about nine indicators of teaching quality: teaching for relevance, acknowledge negative feelings, participation encouragement, using a non-controlling language, provide optimal challenge, focus on the process, structure the class, provide positive feedback, and caring. Scales were rated on a 7-point Likert-type scale, ranging from 1 (I do not agree at all) to 7 (I strongly agree). To examine factorial validity, we performed a confirmatory factor analysis (CFA) for each variable. Information about the estimation method and missing data is extended in Data Analysis section. To examine reliability, we used McDonald’s omega.

Teaching quality was assessed with 31 items (e.g., “My teacher asks for our opinion to pose more entertaining class tasks) from the scale developed by León et al. (2017). These items cover students’ perception of nine concrete and specific teachers’ behaviors: teaching for relevance, acknowledge negative feelings, participation encouragement, using a non-controlling language, provide optimal challenge, focus on the process, structure the class, provide positive feedback, and caring. McDonald’s omega for factors ranged from .78 and .89.

Task-expectancies and task-values in math were assessed with seven items (e.g., “I think I can be successful in my math class” or “I think my math class is important”) from the Expectancy-Value-Cost instrument developed by Getty et al. (2017). McDonald’s omega was .92.

Effort-regulation was assessed using four items (e.g., “When work is difficult, I either give up or study only the easy parts”) from the effort regulation subscale of the Motivated Strategies for Learning Questionnaire (Pintrich et al., 1993). McDonald’s omega was .83.

Connection frequency were addressed with three items (e.g., “When you study for tests or exams, how often do you relate the class contents with other things in your life?”) developed by Hulleman et al. (2017). We used a 7-point Likert-type scale, ranging from 1 (never) to 7 (all the time) to rate the scale. McDonald’s omega was .80.

Future interest in math was assessed with three items (e.g., “I am interested in taking more math classes in the future”) from the Future Interest in STEM items proposed by Getty et al. (2017). McDonalds’ omega was .83.

Data Analyses

To explore the effect of teachers’ behaviors on students’ outcomes analyses should take into account the nested nature of data (Marsh et al., 2012; Stapleton et al., 2016). Thus, although students’ perception of teachers’ behaviors at individual level is an indicator of students’ individual perceptions and mental representation of the class, at group level, it is understood as teaching quality (León et al., 2018). However, even though many authors have tested how math teachers can enhance students’ learning, unfortunately, they usually have not accounted for the nested nature of data.

Consequently, in this study we tested our hypotheses running a multilevel structural equation model (MSEM), where teaching quality predicted students’ expectancy and value, and these, in turn, predicted students’ connection frequency, effort, and interest in math. Following Marsh et al. (2012) guidelines, in our model we deal with contextual variables (students’ class-average task-expectancy, class-average task-value, class-average effort, class-average connection frequency, and class-average interest), and climate variables (indicators of teaching quality). Contextual variables are those based on values assigned according to individual characteristics, and they are group-level aggregations of student-level variables which are specific to students in the same class. By contrast, climate constructs result from asking students about a common variable in the same class, so they are not based on individual characteristics but on a common reference for all of them (in our study, teachers’ behaviors). In this study, we aimed to test the relationships between climate and contextual variables. Introducing these variables at both levels allows obtaining more information about them (Morin et al., 2014) and separating the variance between the two levels of analyses (Friedrich et al., 2015).

To test the meditational effect of students’ expectancy-value between teaching quality and students’ connection frequency, effort, and interest, we computed unstandardized indirect effects and its standards errors using the delta method (Sobel, 1982), and through using separate models to reduce complexity of the model. To conduct mediation analyses, we followed recommendations of MacKinnon (2008) and Hayes (2018).

Since variables were ordered categorically, we used a weighted least square means adjusted (WLSM) estimator, which is more accurate than the maximum likelihood method (Schmitt, 2011). We handled missing data using the WLS estimation method, since it provides robust estimates under some common assumptions of missing data (Asparouhov & Muthén, 2010). The analyses were conducted using Mplus 8.2 software (Muthén & Muthén, 2017).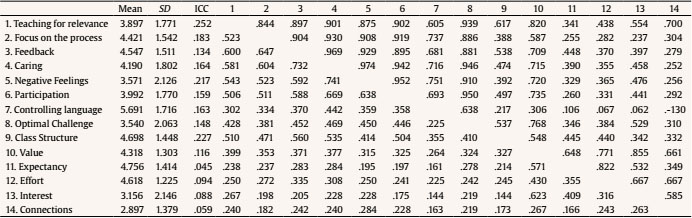

Results

Preliminary Analyses

Means, standard deviations, intraclass correlations, and correlations between major variables are shown in Table 2. Means varied between 2.897 (Connections) and 5.691 (Controlling language), and standard deviations between 1.225 (Effort) and 2.146 (Interest). Regarding correlations, they ranged from .144 (Interest with Controlling Language and Interest with Class Structure) to .741 (Caring with Negative Feelings) at individual level, and from .-130 (Connections with Controlling Language) to .974 (Caring with Negative Feelings) at between level. ICC varied between .045 (Expectancy) to .252 (Teaching for relevance). ICC values close to 1 indicate agreement between students in the same class and that variance is due to the group, while values close to 0 indicate that variability is due to individual differences between subjects and not to the group.

Teaching Quality and Students’ Expectancy-Value, Connection Frequency, Effort, and Interest

We tested the hypothesized model, in which Teaching Quality predicts students’ Expectancy and Value and this, in turn, predicts students’ Connection Frequency, Effort and Interest.

Chi-squared test and fit indexes for the MSEM were χ²(1112, 2256) = 268877.650, p < .001, RMSEA = .068, SRMRwithin = .052, SRMRbetween = .168, CFI = .959, TLI = .957. As depicted in Figure 2, at group level, Teaching Quality predicted Expectancy (β = .415, SE = .116, p < .001), and Expectancy predicted Connection Frequency (β = .191, SE = .166, p <.001), Effort (β = .536, SE = .076, p < .001), and Interest (β = .503, SE = .085, p < .001). At group level, Teaching Quality also predicted Value (β = .695, SE = .063, p < .001), and Value predicted Connection Frequency (β = .537, SE = .142, p < .001), Effort (β = .461, SE = .086, p < .001), and Interest (β = .567, SE = .077, p < .001). At the individual level, Teaching Quality predicted Expectancy (β = .418, SE = .023, p < .001), and Expectancy predicted Connection Frequency (β = .194, SE = .024, p < .001), Effort (β = .368, SE = .023, p < .001), and Interest (β = .229, SE = .025, p < .001). At this level, Teaching Quality also predicted Value (β = .545, SE = .020, p < .001), and Value predicted Connection Frequency (β = .414, SE = .029, p < .001), Effort (β = .554, SE = .021, p < .001), and Interest (β = .633, SE = .016, p < .0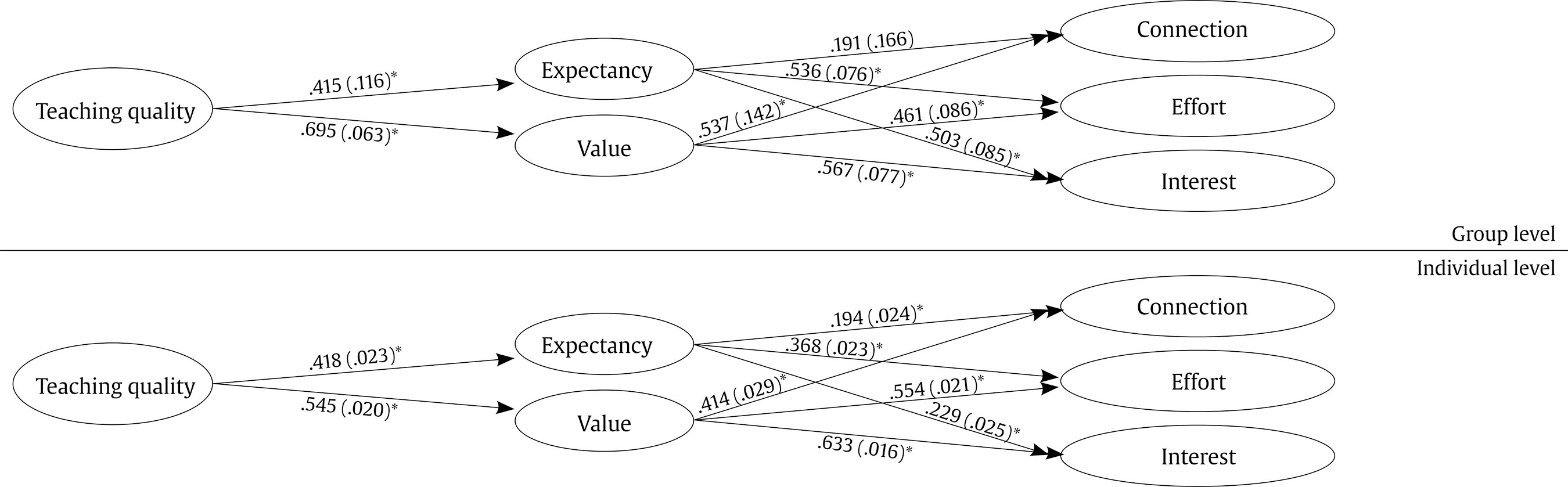01).

Indirect Effects

Regarding the indirect effect of students’ Expectancy-Value in the relationship between Teaching Quality and Connection Frequency, the unstandardized effect was significantly different from 0 at the individual level (β = .330, SE = .064, p < .001) and at the group level (β = .682, SE = .254, p= .007). Secondly, concerning the indirect effect of students’ Expectancy-Value between Teaching Quality and Effort, the unstandardized effect was also significantly different from 0 at the individual level (β = .391, SE = .049, p < .001) and at the group level (β = .529, SE = .140, p < .001). Lastly, regarding the mediational effect between Expectancy-Value and Future Interest, the unstandardized effect was, likewise, significantly different from 0 at the individual level (β = 2.696, SE = .311, p < .001) and at the group level (β = 1.321, SE = .300, p < .001).

Discussion

Building on prior research on teaching quality and expectancy-value theory, this study set out to analyze, on the one hand, the effect of teaching quality as a predictor of students’ task-expectancies and task-value. On the other hand, we aimed to test how task-expectancies and values predicted students’ connection frequency, effort, and future interest in math. Our findings extend previous research that analyzed how teaching quality predicts students’ motivation and other performance-related variables. However, to the best of our knowledge, never before it has been examined how teaching quality is related to students’ expectancy-value motivation, and how this, in turn, relates to students’ connections, effort, and future interest in math. Exploring how teaching quality can enhance students’ math learning is especially useful for educational researchers and secondary education teachers, since it helps to design interventions to improve students’ optimal functioning in the subject, commonly poor and unsuccessful at this stage (Kiemer et al., 2015).

This study provided support for the hypotheses tested. First, teaching quality - specifically teaching for relevance, acknowledge negative feelings, participation encouragement, using a non-controlling language, provide optimal challenge, focus on the process, structure the class, provide positive feedback, and caring – predicted students’ expectancy-value motivation (Hypothesis 1). Second, students’ connection frequency, effort, and future interest in math were predicted by their task-expectancy motivation (Hypothesis 2). Third, students’ connection frequency, effort, and future interest were predicted by their task-value in math (Hypothesis 3).

On the one hand, we provided evidence of the relationship between teaching quality and students’ task-expectancies and value motivation. Although previous research has widely explored the influence of teachers on students’ learning (Wallace et al., 2016), and it has been previously shown that expectancy and value motivation are shaped through the learning context (Gaspard, 2015), less is known about how math teachers behaviors in class are related to students optimal functioning (Rimm-Kaufman et al., 2014). Our findings could be considered consistent with few studies, also conducted within the Self-determination theory, that have used the same approach to assess teaching quality in relation to other motivational constructs. Thus, based upon León et al.’s (2017) global approach to teaching quality, different studies have analyzed how high school students’ perceptions of their math teachers’ behaviors affect students engagement (León et al., 2017), effort-regulation (León et al., 2017), and passion toward math (Ruiz-Alfonso & León, 2017, 2019). As we did, authors in these studies took into consideration the nested data structure, so their findings were not just reflecting students’ perceptions at individual level, but also the teaching quality at class level (Marsh et al., 2012). In this regard, our findings may contribute to methodological issues surrounding research on teaching quality and expectancy-value. Most of the studies on this topic have not considered the multilevel methodological approach, so, unfortunately, their findings could be interpreted as reflecting individual rather than contextual differences (Hospel & Galand, 2016).

On the other hand, our results could also be consistent with other studies that have similarly suggested positive relations between teachers’ functioning and students’ outcomes within the expectancy-value framework. Becker et al. (2014), for example, assessed how teachers’ instructional behaviors based on value-induction affected students’ intrinsic value, and in turn, students’ emotions. Similarly, most relevant research drawing on Eccles’ Expectancy-value theory have focused on interventions conducted to increase students’ beliefs about the content they are learning, findings reporting that students in the utility value condition displayed, among others, higher levels of interest, future intentions, and academic performance (Durik et al., 2015; Hulleman et al., 2016). Although these interventions highlight the importance of stressing the relevance of school contents, and it is a teaching quality indicator, they have been usually carried out by researchers that have assessed how students outcomes varied through the manipulation of students’ task-values. However, they did not specifically test students’ perceptions of their math teachers. Also within the expectancy-value framework, Wang (2012) found that students’ perceptions of math classroom characteristics – including teachers’ expectations, teachers social support, or teaching for meaning – affected students’ expectancies and subjective task-values and, in the long term, students’ educational and career aspirations regarding math areas. In a recent study, Lazarides et al. (2019) also found that students’ perception of teachers’ instructional clarity was related to adaptive motivational changes in students, and that students when perceiving high instructional clarity were less likely to lose their mathematics intrinsic value and interest. However, most of the previous studies and relevance interventions have mainly focused on value but not on expectancy (e.g., Durik et al., 2015, Hulleman & Harackiewicz, 2009; Lazarides et al., 2019), maybe because value seems to be more easily influenced from the context, and it is easier for educators to stress the relevance of learning material rather than foster expectancy beliefs (Gaspard, 2015). Besides, most of the research has only focused on a few indicators of teaching quality and, which is more important, they have not taken into account the nested nature of data.

Finally, we provided evidence of the association between students’ expectancy-value motivation and their connection frequency, effort, and future interest in math. These findings fit well within Eccles’ (1983, 2009) theory and are consistent with other studies that have explored these relations. In the model tested in our study, we suggested that finding the material useful and students’ beliefs about their capacities will lead them to put more effort into the activity, to generate more connections, and to be more interested in the subject. Part of these findings are in line with earlier studies that have suggested that task-value promotes interest (Durik et al., 2015; Getty et al., 2017; Hulleman et al., 2017), connection frequency (Hulleman et al., 2017), and effort-regulation (Dietrich et al., 2015; Dietrich et al., 2017; Kusurkar, Croiset, et al., 2013; Lazarides et al., 2019). However, these relations have not always been analyzed in the same direction. For example, Hulleman et al. (2017) found, through an intervention with undergraduate students, that improving students’ value perception led them to make more connections and thus, in turn, to become more confident about their abilities to learn the material and to increase interest toward the course. Although most evidence supports the role of expectancies and values for predicting students’ outcomes (Gaspard, 2015), more research is needed to clarify the mechanisms underlying these relations.

To summarize, as was expected, this research provides evidence of the relationship between teachers’ behaviors and students’ expectancy-value motivation. We also shed light on the relationship between students’ expectancy-value motivation and their connection frequency, interest, and effort regulation in math. For the first time in the literature, regarding mathematics and the variables tested, we conducted this study assessing particular indicators of teaching quality and taking into account the nested data nature, our findings contributing to the existing literature on teaching quality and expectancy-value motivation academic outcomes.

Limitations and Future Research

Despite the novel features of our study, our findings should be understood by accounting for several limitations. First limitation refers to the nature of the study. We conducted a cross-sectional design that made it impossible to establish causal relationships between the variables tested. Although previous research provides evidence of the role of teaching quality on students’ motivation, and supports the role of expectancies and values in academic outcomes, through our findings we cannot provide accurate information about the direction of the effects. We propose for future studies to conduct longitudinal studies to test these relationships.

Second, we used students’ perceptions as a single measure of teachers’ behaviors. Although aggregated students’ perceptions are considered as reliable measures of classroom characteristics (Morin et al., 2014; Wentzel et al., 2017), and what most influences students’ outcomes is how they perceive their teachers and classroom environment (Reeve, 2002; Stroet et al., 2013), we propose for future research to include other approaches such as teachers’ own perceptions and external observers’ ratings.

Third, in our model we did not control for potential confounding covariates that could intervene and explain some of the variance in dependent outcomes. According to previous literature, sociodemographic variables (such as teachers and students’ age and gender, teachers’ years of experience, students’ ethnicity, and parents education and occupation), and achievement-related variables (such as students’ well-being or previous performance) warrant consideration as covariates due to their association with students’ motivation and academic adjustment. Consequently, researchers are cautioned to test in future studies more complex models that could consider these covariates. In addition to include potential confounding variables in the model, researchers could also try a stratifying or matching procedure (see Rohrer, 2018, for a review).

Fourth, we encourage future research to test our hypotheses conducting educational interventions in line with those developed by Hulleman et al. (2010), Hulleman et al. (2017), and Hulleman and Harackiewicz (2009). Through these interventions, we could determine if changes in dependent variables (in our study, students’ effort, connection frequency, and interest) could be explained by changes in the independent variable (in our study, teaching quality). Also, it could be interesting to test if mediating variables (in our study, students’ expectancy and value) could be understood as mechanisms to establish clear connections between the variables tested (Kazdim, 2007).

Finally, we also encourage future studies on teaching quality and expectancy-value motivation to carry out their analyses taking into consideration the nested nature of their data. When researchers aim to assess how teachers, classroom, or school characteristics affect students’ outcomes, they are assessing, at individual level, students’ perceptions of teachers’ behaviors. However, also introduced at the classroom level, findings will more accurately reflect contextual influences.

Implications for Education

This study provides practical implications for schools and teaching practice. Considering our results and those of previous research that has shown that students’ expectancy and value motivation are largely shaped by their learning environment (Gaspard, 2015), we encourage educators to be aware of the importance that their behaviors acquire in students’ motivational and performance outcomes. Appreciating the relevance of a variable amenable to intervention, such as teaching quality, allows us to reckon that there is still much room for improvement in optimizing students’ math learning.

In this study, we analyzed under the label of teaching quality how specific teachers’ behaviors contribute to students’ motivation enhancement. Although our findings must be supported by future studies to establish causal relationships between variables, in view of previous literature supporting the role of teaching quality in students’ motivation, we recommend teachers: to “teach for relevance” (underscoring the usefulness and relevance of the class contents, as well as the practical application of those contents in other subjects or in students’ daily life); to “acknowledge students’ negative feelings” (trying to understand the negative emotions arisen, for example, when students feel anxious when dealing with an exam or a difficult activity); “to encourage students’ participation in class” (for example, by asking students’ interests or points of view about a new topic); “to do not use a controlling language” (avoiding the use of a directive language versus talk to students in an informational and gentle tone); “to provide optimal challenge” (for example, assigning activities accounting for different students’ level); “to focus on the process” (for example, valuing the process and not only the final result obtained by students in a math problem); “to structure the class” (for example, preparing in advance the session’s structure and contents, and giving students’ clear information about them at the beginning of the session); “to provide positive feedback” (guiding students through specific and constructive instructions, firstly explaining to them what they have done well and, then, what and how they should improve); and “to provide care about the students” (showing concern for students, feeling interested, for example in what they like to do outside the school or how they feel in class). Although much more research is still needed on this topic, it could also be interesting for schools to propose intervention programs to guide math teachers in the acquisition of teachers’ behaviors that promote students’ optimal learning in the subject.