The Moderating Role of Mathematical Skill Level when Using Curricular Methods to Learn Multiplication Tables

Introduction

The mastery of single-digit multiplications (such as 3 x 4) is probably within the minimum targets of most educational systems around the world (e.g., see National Mathematics Advisory Panel [NMAP, 2008] in the USA; EURYDICE, 2011, for the European Union). This is a natural consequence of the fact that multiplication plays an important role in everyday life and that poor computational fluency leads to overall deficiencies in mathematics (Kilpatrick et al., 2001; NMAP, 2008), thus compromising not only students’ school performance but their future professional status (e.g., Dowker, 2005; Geary, 2011; NMAP, 2008).

Traditionally, it is assumed that curricular methods aimed at learning multiplication at school should provide children with: i) a conceptual understanding of the arithmetic operation and ii) fluency, that is, the skill of solving single-digit multiplications quickly and accurately. Understanding the meaning of multiplication is fundamental in our daily lives, but developing fluency is also needed, as this allows students to free-up cognitive resources that will be necessary when, in subsequent years of learning, more complex computations such as multi-digit multiplications or divisions are encountered (e.g., Bryant et al., 2008; Carr et al., 2011; Dowker, 2005; Fuchs et al., 2008; Geary, 2011; NMAP, 2008).

Different approaches to the teaching of single-digit multiplications are used in various parts of the world, but in that their objective is to attain a certain level of fluency they usually share the common feature that learning should rely mainly on memory. The focus on memorization is based on evidence that, as a means of solving single-digit multiplications, this is the most efficient, fastest, and least error-prone strategy (Ashcraft, 1992; Dowker, 2005; Siegler & Shipley, 1995; Steel & Funnell, 2001). To this end students are usually asked to recite the multiplication tables exhaustively in order, and to practice problem solving (e.g., Blanco-Solórzano, 2020; Dowker, 2005; Fernández, 2007). Sometimes this is complemented with additional procedures, these also based in memory, such as the rehearsal of individual problems (e.g., Nelson et al., 2013; Powell et al., 2009) or ‘cover-copy & compare’ tasks (e.g., Codding et al, 2011). Curricular methods applied in schools differ in terms of the extent to which all the tables (the matrix of 10 x 10 operations, or even the matrix of 12 x 12 operations), or a subset of these, are memorized (e.g., Woodward, 2006). For instance, in most western countries all the tables are learned, whereas in China multiplication tables typically include only smaller-operand-first entries (e.g., 4 × 9 = 36, but not 9 × 4) (e.g., Campbell & Xue, 2001; Zhou et al., 2007). So, the most conventional curricular methods emphasize memory as the main way of learning the tables, whereas in other curricular methods only certain tables are learned through memorization, applying rules consistently (e.g., the commutative principle) to solve the remaining problems (e.g., Isaacs & Carroll, 1999; Miller et al., 1996).

Although rote verbal memory and repeated practice are the basis of most conventional methods aimed at teaching multiplication, such strategies are not without difficulties. First, many children simply struggle to learn multiplication using these strategies (e.g., Dowker, 2005; Geary, 2006; Jordan et al., 2003; Lemaire & Siegler, 1995, NMAP, 2008). Second, these strategies imply a significant investment in time for both teachers and students. Therefore, assessing the effectiveness of conventional methods and/or designing new ones based on scientific evidence is needed. Unfortunately, experimental support for curricular methods designed to teach multiplication in the classroom is scarce (e.g., NMAP, 2008). This paucity of evidence stands in clear contrast to the existing literature on intervention, in which either one or a combination of instructional strategies are applied during certain weeks only, sometimes by specialized professionals (e.g., psychologists), and focus on partial results (the learning of a small set of operations) (e.g., Brendefur et al. 2015; Kaufmann & Pixner, 2012; Nelson et al., 2013; Woodward, 2006; see also Codding et al., 2011, for a review and meta-analysis on intervention strategies).

The outlook in the area of designing new curricular methods based on scientific evidence is becoming more positive thanks to collaboration between researchers and practitioners. Cognitive and educational psychologists are currently offering new insights into the mechanisms involved in mathematical learning, and this knowledge is available to be employed in developing new educational methods (Star & Rittle-Johnson, 2016; see also Alcock et al., 2016). Looking specifically at the process of solving multiplications, psychologists have recently demonstrated the importance of interference in learning and retrieving multiplication problems. De Visscher & Noël (2013, 2014a, 2014b, 2015; see also De Visscher et al., 2015) have exhaustively analyzed the role of interference in storing and accessing multiplication tables. According to these researchers, an increased sensitivity to interference would explain the persistent difficulties that some children experience in solving single-digit multiplications. As explicitly assumed in Campbell’s Network Interference Theory (Campbell, 1995), multiplications are characterized by their similarity at both the physical and the magnitude level; that is, 4 x 6 and 4 x 7 are physically similar, and the quantities represented by their solutions (respectively 24 and 28) are also similar (e.g., Campbell, 1995; De Visscher & Nöel, 2013, 2014a, 2014b, 2015; Geary, 2006; Kaufmann et al., 2004). So, when a problem is presented, it also activates similar related problems. All such problems compete by mutual inhibition with strength of activation determined by similarity to the presented problem. That is, similarity between problems has the potential to cause interference in learning and retrieving multiplication problems, and would explain why most errors made in solving multiplications are table-related (that is, an incorrect response is correct for another single-digit multiplication in the same time-table: 4 x 8 = 36; e.g., Barrouillet et al., 1997; Butterworth et al., 2003; Campbell & Graham, 1985). To support the role of interference in multiplication learning, De Visscher and colleagues developed an index of the physical similarity between multiplication problems. This index was able to explain the variability in achievement across problems in third and fifth graders and undergraduates above the classical problem-size effect (i.e., response times and errors are greater in problems with larger operands, hence it is easier to solve 3 x 4 than 8 x 9). So, it seems that a fundamental component of successful multiplication learning involves being able to cope with interference, and not all children seem to show the same aptitude here (De Visscher & Noël, 2014b). Also, of interest for the learning process is the fact that interference increases with the number of problems to be memorized (Lemaire & Siegler, 1995). This is known as retroactive and proactive interference and implies both that the learning of new problems impairs the learning of the old ones (see McCloskey & Cohen, 1989) and that the previously learned problems impair the learning of the new ones (e.g., Campbell & Graham, 1985).

The evidence reviewed above suggests that educational strategies aimed at reducing interference should facilitate the learning of multiplication. An easy way to diminish interference in multiplication retrieval is to reduce the set of problems to memorize (i.e., fewer problems, less competition), and rules can help here. By using rules for some tables (1 and 10), as well as the commutativity principle, the matrix of 10 x 10 problems can be reduced to 36 problems to be memorized. Relying on rules to learn some multiplications is not new. However, the recent literature has shown that “using single-step rules” allows children to rapidly obtain the solution to a problem without the effort of executing complex multi-steps procedures or memorizing facts by pure association (Baroody, 1983; Uittenhove et al., 2016).

Taking this as starting point, we designed and applied a new teaching method. With the aim of reducing interference, it combines the learning by “memory” of a reduced set of problems with the use of “rules” (from now onwards, M&R method). Moreover, to help with the memorization of the problems, along with fact rehearsal and guided practice, we added a portable time-tables. The rationale for this is that it may work in a similar way to flash cards, which in primary education have been shown to facilitate learning and to promote a sense of control over learning (e.g., Hulac et al., 2012; Teng & He, 2015). Additionally, in the portable time-tables we coded tables with colors. According to sensory integration theories, as well as previous evidence here (see e.g., Domahs et al., 2004; Kaufmann & Pixner, 2012), establishing color cues in memory seems to help people to retain problems. By cueing each times tables with a different color, we expected to facilitate the building of the multiplication network.

On the other hand, to help with the learning and use of rules the M&R method promotes not only the mechanistic learning of single-step rules; it also encourages the understanding of these rules, because conceptual understanding constitutes greater achievement than simply heuristic learning (e.g., Rittle-Johnson et al., 2001). It should be noted that the M&R method was not designed from scratch, but rather is based on curricular methods already employed in some countries (e.g., China: Campbell & Xue, 2001; Zhou et al., 2007) and also seen in previous studies (e.g., Isaacs & Carroll, 1999; Miller et al., 1996; Woodward, 2006), but here we give a rationale for the use of such practices from a theoretical point of view, and also incorporate into the method some ideas from educational and cognitive psychology.

The M&R method was compared to a conventional one, that is, a method that, once the concept of multiplication had been explained, was based on the memory-based learning of the whole multiplication table. With this aim in mind, it uses fact rehearsal and guided practice as the main strategies (see Table 1 for a comparison of the strategies used in each method; see also a more detailed description of both conventional and M&R methods, in the Method section).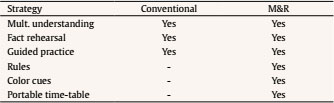

Multiplication Learning and Individual Differences

An additional aspect of the present study has to do with individual differences in multiplication fact learning. Educational systems inevitably have to deal with the issue of diversity in the student population; teaching methods that are valid for some students are not always useful for others (Riding, 2007). So, it is necessary to identify those individual characteristics of children that are likely to increase the probability of a successful application of a method (e.g., Connor et al., 2018).

From a cognitive perspective, differences in arithmetic learning have been related to differences in the mechanisms of working memory, either globally (e.g., Bull et al., 2008; Davis & Kelly, 2003; Geary, 2006) or in any of its slave systems, such as the phonological loop (see e.g., Lee & Kang, 2002; Schleepen et al., 2016; Swanson & Sachse-Lee, 2001) or the visual sketch pad (see e.g., Bull et al., 2008; McLean & Hitch, 1999; Passolunghi et al., 2007). Developmental studies have also shown the role of executive functions in predicting math learning at school (e.g., Bull & Scerif, 2001; Bull et al., 2008). As noted above, control of interference seems to play a very significant role in explaining individual differences in memorizing multiplications tables (e.g., De Visscher & Noël, 2014). Importantly, together with cognitive factors (e.g., phonological memory), basic numerical skills like the comparison of dots and Arabic numbers have also been connected to multiplication fluency (Schleepen et al., 2016; see De Smedt, 2016 for review), pointing out the relevance of also considering the previous mathematical knowledge of children when facing the learning of multiplication time-tables (see more on this below).

Experiential factors have also been related to differences in mathematical attainment. For instance, children with low socio-economic status (SES) suffer from reduced exposure to situations involving numeracy, and this may affect the normal development of their mathematical skills, including multiplication (Perry & McConney, 2010). Motivation may also play a role in this relationship; Hoffman (2015) has suggested that children’s motivation acts as a modulator in the multiplication learning process.

Finally, and most importantly for the current study, the literature on interventions aimed at increasing fluency in arithmetic has also identified the importance of individual differences in levels of mathematical skill relating to how students take advantage of different interventions. Children with poor accuracy in multiplication tasks respond better to interventions that focus on modelling, and those who show acceptable accuracy but poor fluency respond better to interventions that focus on repeated practice (Nelson et al., 2013). Another characteristic which, despite its relevance here, is usually not addressed in research is students’ overall level in mathematics. It seems reasonable to assume that a more comprehensive background in math might lead to a more focused approach to multiplication whereas a reduced mastery of math might require a more diverse approach. Within the scant experimental evidence here, Woodward (2006) has shown that children with strong mathematical skills benefitted more from conceptual instruction than those with poor skills. Clearly, additional research in this area is needed (Nelson et al., 2013). It is beyond the scope of the present research to cover all the factors related to individual differences in multiplication learning. However, due to its relevance, an additional aim of the current study is to analyze the impact that participants’ mathematical skills have in explaining the impact of different learning methods. Exploring the relevance of children’s individual differences in mathematical skills can pre-emptively direct practice by targeting those children who respond better to one method or another (e.g., Connor et al., 2018).

The Current Study

In this study we address two research questions related to the effectiveness of curricular methods aimed at attaining certain levels of fluency in solving single-digit multiplications: a) does a method aimed to reduce interference, the M&R, which combines memory retrieval and single-step rules, lead to greater achievement than a conventional method based on memory retrieval of the whole time-table? b) to what extent is the effectiveness of these methods moderated by children’s levels of mathematical skills?

To answer these questions, we compared the effectiveness of the M&R method, which seeks to reduce interference through combining memory and rules, with a conventional method, but paying attention to the modulator effect of children’s mathematical skills. Notably, our study compared curricular methods, i.e., comprehensive methods aimed at teaching multiplication and attaining fluency with time-tables in the classroom and did not involve the comparison of small intervention methods simply aimed at achieving fluency in a small subset of multiplication facts or in a special population.

We employed moderation analysis (based on linear regression analysis; see Hayes, 2013, for example) to test our hypotheses. Moderation analysis provides evidence not only of the relationship between two variables, in this case between a predictor, the type of method, and an outcome (multiplication fluency), but also under which circumstances it occurs, here the values of mathematical skills. In this sense, moderation is similar to the concept of interaction (Fairchild & McQuillin, 2010; Hayes, 2013). Moderation analysis also has the advantage of using continuous variables (in this case, mathematical skills) and thus avoids the lack of power associated with artificially categorizing participants in groups (Cohen, 1983), as would have been the case were we to have used an ANOVA.

As we will note in the description of the M&R method (see below), there is theoretical and experimental support for: i) limiting the number of problems to memorize as a means of reducing interference; ii) the effectiveness of single-step rules in providing fast and accurate solutions to arithmetical problems; iii) the relevance of conceptual understanding in learning math; and iv) the benefits of using complimentary material, such as flash cards (equivalent to the portable time-table) and using color cues, in multiplication learning. So, it is hypothesized that students following this method should outperform those on the conventional method. Less certain is the question of the role of mathematical skills in terms of benefiting from the conventional and the M&R methods. Previous studies have suggested that children with poor skills benefit from strategies based on memory retrieval, such as conventional ones, which include practicing and modelling at the same time (Codding et al., 2011; Geary, 2004; Nelson et al., 2013) but there is also evidence that methods based on conceptual strategies increase fluency to the same extent (e.g., Gray et al., 2000; Mulligan & Mitchelmore, 2009; Woodward, 2006) and may even provide better outcomes than methods based on drill learning (e.g., Brendefur et al., 2015). Taking into account the principles on which the M&R method is based, we hypothesized that it will be more effective than the conventional one, and that this will be more evident in those children with low mathematical skills, because, together with practice and understanding, it provides easy single-step rules that should facilitate learning by reducing interference. Additionally, the benefits of the M&R method (which involves more guidance), as compared to the conventional one, may be smaller on children with high mathematical skills, in line with the expertise reversal effect (e.g., Chen et al., 2016; Kalyuga et al., 2003; Nihalani et al., 2011).

Method

Participants

The respondents were 160 children (89 girls) aged 7-8 years, all of whom were second grade students in a charter school in Malaga (Spain). Children were from diverse socio-economic backgrounds, but most were from a medium socioeconomic level. An additional group of eighteen students diagnosed with developmental disabilities (i.e., dyscalculia, dyslexia, attentional problems) took part in the study, but were excluded from the analyses. Participants were drawn from 8 different classrooms. In four of these (80 children, 41 girls) the conventional procedure was followed during the 2014 academic year, and in the other four classrooms (80 children, 49 girls) the M&R method was followed in 2015. However, in both cases the methods were applied while children were in second grade. Informed consent for children was obtained thorough the school’s staff.

Materials and Procedure

The two multiplication methods were followed for 6 months (January to June) as part of children’s second grade math classes. Both groups were evaluated at the end of the school year, after having finished the method.1

A mathematical skills test (BERDE: Batería para la Evaluación Rápida de la Discalculia Evolutiva [Battery for Rapid Evaluation of Developmental Dyscalculia]; García-Orza et al., 2014; see www.ladiscalculia.es) was used to determine the mathematical skills of each student. BERDE is designed to explore basic numerical skills in students from grades one to six. It provides an assessment of different mathematical skills, including dot and Arabic comparison tasks, number line tasks, counting and serial ordering, Arabic number writing to dictation, single-digit addition, subtraction and single-digit multiplication. In the dot comparison, Arabic comparison, and addition and subtraction tasks, participants were asked to solve as many problems as possible in a fixed period of time (1 minute for the comparison tasks, 2 minutes for the arithmetic tasks). In the transcoding task and the counting and serial ordering tasks, participants had no time limit to solve the subtests. A factorial analysis of the data on the test revealed a structure with two factors, one related to the comparison of quantities, other related to numerical-verbal skills. This resembles the original structure of the test, validated with children from first to sixth grade. Internal consistency of the factors, as measured by Cronbach’s alfa, was .71 for the first factor and .60 for the second. For this study, a global math score (excluding the score in the multiplication task) was obtained for each participant. This score consisted of the sum of the scores obtained for all the tasks (excluding multiplications). Comparisons of the math skills between groups did not show significant differences (see Table 2).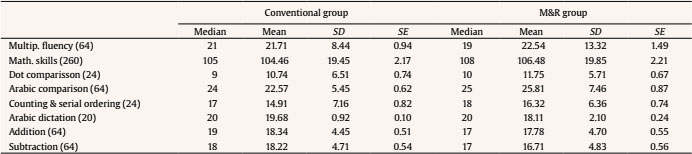

To assess multiplication fluency, the multiplication fluency test of the BERDE was used in a different session. Children were provided with a booklet including two sheets with single-digit multiplications in two columns, with 15 problems in each column, for a total of 60 problems. Ties problems (e.g., 3 x 3), smaller-operand first (e.g., 3 x 7), and larger-operand first problems (e.g., 7 x 3) were included in the set. Problems were semi-randomly ordered with the aim of avoiding the consecutive appearance of the same problem with a different order. It was explained to the children that they had two minutes to solve as many problems as they could. Instructions stressed that problems should be performed in columns and that no problems could be skipped. The score was calculated as the number of problems correctly solved minus those solved incorrectly.

The Curricular Methods

First, we note that both methods described here emphasize the practice of fact retrieval as a key active component, and both use the same textbook (Labarta et al., 2011), Matemáticas 2 Primaria. Conecta con Pupi [Mathematics 2^nd grade. Connect with Pupi], SM Editorial. However, whereas in the M&R method this was used as complementary material (it was mainly used as an activities database), in the conventional method it was the main guide for learning. This difference involved that rules, including the commutative principle, and time-tables, were presented in a different temporal sequence and with different purposes in each method (see below for more details on this). In both cases the children practiced retrieval with the exercises in the textbook and with additional work-sheets, and these materials were always adjusted to the lesson in question. The textbook includes sections which explain the concept of multiplication as repeated addition, then the tables, and finally the commutative rule is briefly explained. The main differences between methods are described in the following sections.

The Conventional Method

The basis of this method is memorizing the tables from 1 x 1 to 10 x 10 through the use of rote verbal learning and repeated practice with problems. Although during the learning process some conceptual knowledge is presented, and it is usually pointed out that some tables can be learned by rules, the time-tables with all the problems are ultimately learned by memorization.

Three phases were included in this method. During the first phase the concept of multiplication was explained to children using verbal and visual examples. They were also asked to convert repeated additions into multiplications (e.g., 3 + 3 + 3 + 3 + 3 = 5 x 3). In the second phase the rote verbal learning of tables from 1 x 1 to 10 x 10 was stressed by reciting the sequences in the classroom and by practicing problems. Following the textbook, the 2 and 4 time-tables were learned first, then 1 and 10, followed by 5, and finally 3, 6, 7, 8, 9, and 0. For the learning of each time-table, the procedure in the classroom was as follows: initially the table was presented and was recited by all children several times. They were then provided with time to recite the table themselves, to practice problems, and to study it at home. During the following schooldays they were asked the table in full and also in individual problems presented verbally or in a booklet. After a variable delay, according to what the teacher considered appropriate, the learning of a new table was presented. Finally, in the third phase, once all the tables had been studied, the children were presented periodically with single-digit problems to be solved as part of math class activities, and then the commutative rule is explained.

With some minor variations, this is the method followed by the majority of schools in Spain (Aguilera et al., 2019; Fernández, 2007; Labarta et al., 2011) and in other Spanish speaking countries (Blanco-Solórzano, 2020). It is based on establishing and reinforcing the association between all the problems and their solutions in students’ long-term memory without relying too heavily on the concept of multiplication and its properties.

The Memory and Rules (M&R) Method

This method combines the use of memory learning and single-step rules with the aim of learning to solve single-digit multiplications. It shares with the conventional method the fact that learning by memory provides an efficient way of attaining fluency but emphasizes conceptual understanding and promotes the use of single-step rules in order to reduce the number of problems to memorize, and then the interference associated with this process. Additionally, the method complements the memory learning process by cueing multiplication tables with color in a portable time-table. In this way it seeks to reinforce the association between problems and their solutions (the materials of the method, in Spanish, can be downloaded from www.ladiscalculia.es).

The method is based on educational strategies applied in certain countries (e.g., China) and in response to suggestions in previous research (e.g., Isaacs & Carroll, 1999; Miller et al., 1996); more importantly, it is also based on evidence from cognitive and educational psychology studies. As noted above, multiplication coding and retrieval is hindered by similarities in the material to be stored and retrieved (e.g., Campbell, 1987, 1995; De Visscher & Noël, 2013, 2014a, 2014b, 2015; Dowker, 2005; Verguts & Fias, 2005). A simple way of “reducing interference” is by reducing the number of problems to be memorized, and this can be done easily using rules.

In the M&R method, rules were used to learn the 0, 1, and 10 tables, since their solutions involve a single-step procedure: a x 0 is always 0, a x 1 is a, and a x 10 is a0 ( ‘a’ being any natural number). Additionally, this method used another single-step rule, the commutativity principle: a x b = b x a (a and b being any natural numbers, and a ≤ b), so that only problems in one direction (larger x smaller or smaller x larger) needed to be learned, in this case a x b problems. Instruction was also provided for children, so when faced with problems of the type b x a, they were asked to apply a change of order. By using these single-step rules the method reduces the number of problems to be memorized from the original 100 problems (from 1 x 1 to 10 x 10), to 36 (see Figure 1). Together with detailed explanations of the rules, children were also asked to practice problem solving using these rules, since evidence suggests that practicing rules make them more efficient (e.g., Ericsson et al., 1993). For instance, research in this area has shown a rapid transfer of the knowledge of the solution to a x b problems to b x a problems (e.g., Baroody, 1999).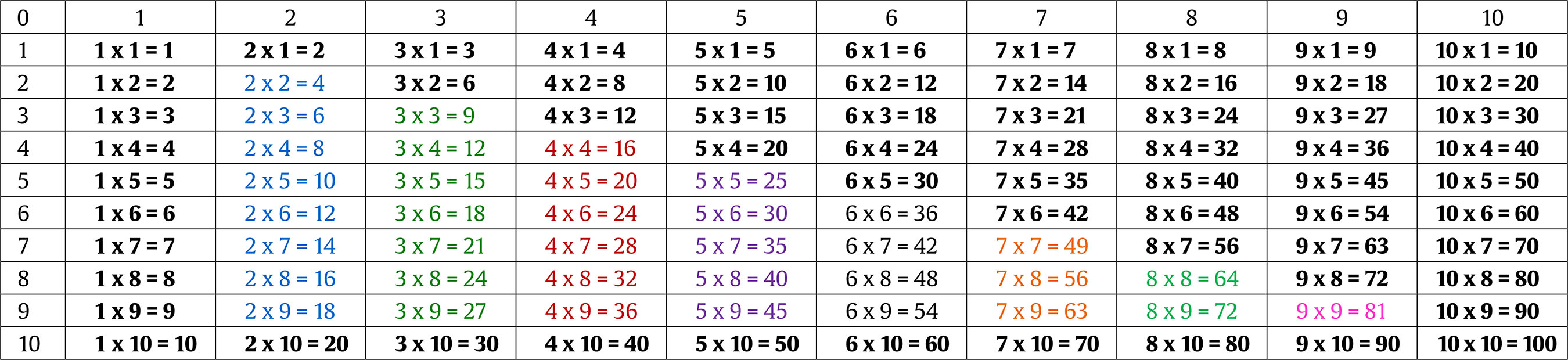

After the application of single-steps rules, children needed to learn a small subset of problems by memory. To help in this process we employed two strategies:

a) A portable time-table was provided for the children (see Figure 1). Printed on half of a DIN A4 plasticized sheet, it included the multiplication tables on one side, each one in a different color, with an indication of those problems to be learned by rote verbal memory, and those (shaded) which were not to be thus learned. On the other side it included the single-step rules described above, as rationale for not learning the shaded problems. Students were asked to take this sheet with them at the end of each day. Simultaneously, poster versions (A1) of this sheet were hung in the classroom. The portable time-table was designed to serve two purposes: to increase the opportunity of repeating the tables at any moment and to increase children’s motivation by pointing out the relevance of learning the tables using extra-curricular material. As summarized in the Introduction, motivational as well as experiential factors play a role in mathematical learning, and although this method does not focus specifically on these topics, the use of the portable time-table tries to address these issues.

b) Problems in the portable time-table were cued with colors. The aim of this was to provide implicit information that is stored in memory and can help children to organize a network of problems. According to some models, during the learning process a network of operator and result nodes is built (e.g., Ashcraft, 1992). In this network, problems that share operands (e.g., 4 x 5 = 20; 4 x 8 = 32) are associated, and this information is also coded in their respective solutions. Previous research has shown the benefits of cueing the learning of multiplication tables with color (e.g., Domahs et al., 2004; Kaufmann & Pixner, 2012).

The application of the M&R method had the following phases: first, children were presented with the concept of multiplication and its understanding was encouraged. As part of this understanding, multiplications by 0 and by 1 were presented. Subsequently, the commutative property was introduced. The last rule presented was the multiplication by 10 rule. Each of these steps was accompanied by the presentation of the time-table and the consequence for memory learning of using this rule. For instance, after understanding the rule for multiplication by 1, these problems were shaded in the portable time-table. After learning the rules of the multiplication tables, the table with shaded problems was presented and children were encouraged to learn by memory those 36 problems that were not shaded, starting with the 2 time-table and moving successively to the 9 time-table. Emphasis was placed on starting each table with the ties (e.g., 2 x 2; 3 x 3, etc.) and using the commutative principle to retrieve the smaller x larger problems (e.g., 2 x 3).

To sum up, the M&R method, as with the conventional method, emphasizes memory in learning the association between problems and solutions. However, it does so on a reduced subset of problems and uses color as an additional cue for recall, whereas for the rest of the problems the method relies on single-step rules. An additional difference between the methods is related to the accessibility of the tables. The portable time-table makes it easier to consult the solution when doubts arise and also makes studying it easier. Moreover, its use as a novel resource probably has the effect of showing children the relevance of learning the tables, and the potential motivational role of the portable time-table as a didactic tool cannot be dismissed.

Design and Analyses

Descriptive statistics were conducted separately for the conventional group and the M&R group. The exploratory analysis indicated that distributions departed from normality, and that homoscedasticity was not attained, so non-parametric statistics were preferred for data analyses.

Non-parametric correlations between mathematical skills and multiplication fluency were developed separately for each group; we also compared the mathematical skills and the multiplication fluency between groups.

A moderation analysis was run to evaluate our hypotheses. This analysis is an alternative to ANOVA for exploring the interaction between the method factor and the level of mathematical skills in predicting multiplication fluency. The moderation analysis was conducted with the Process module by Hayes (2013) for SPSS version 23. This macro uses a non-parametric resampling test that does not rely on the normality assumption and can be used with small samples. Additionally, it includes a procedure to analyze data even when the homoscedasticity of the errors in the estimation of the dependent variable is not assumed (Hayes, 2013). We employed a two-independent group design. The type of curricular method was the independent variable (X), and the scores in the multiplication fluency task were used as a dependent variable (Y). Children’s level of mathematical skills was the moderator variable (M). A detailed illustration of the testing of moderation effects is available in Hayes (2013) see also (Figure 2a). In assessing moderation, the effects of principal interest are b1, b2, and b3, these corresponding to the effects of each factor, and to their interaction, this is, if X’s effect on Y varies with M, respectively (see Figure 2b). The moderator, type of method, was mean-centered prior to the analysis. The categorical predictor type of method was coded as -.50 for the M&R method and +.50 for the conventional group.

Results

Descriptive statistics for the dependent variable and the moderator for each method group are shown in Table 2. A non-parametric test for two independent samples indicated that the mathematical skills of children in the M&R group were similar to those in the conventional group, Z = 0.55, p = .58 two-tailed. Similarly, no differences were observed in multiplication fluency when both groups were compared, Z = 0.99, p = .32 two-tailed.

Overall, the correlation between multiplication fluency and the moderator, mathematical skills, was significant rho = .42 (p < .001). This correlation remained significant when it was analyzed separately in the M&R group, rho = .56 (p < .001), and in the conventional group, rho = .29 (p = .009) (see Figure 3).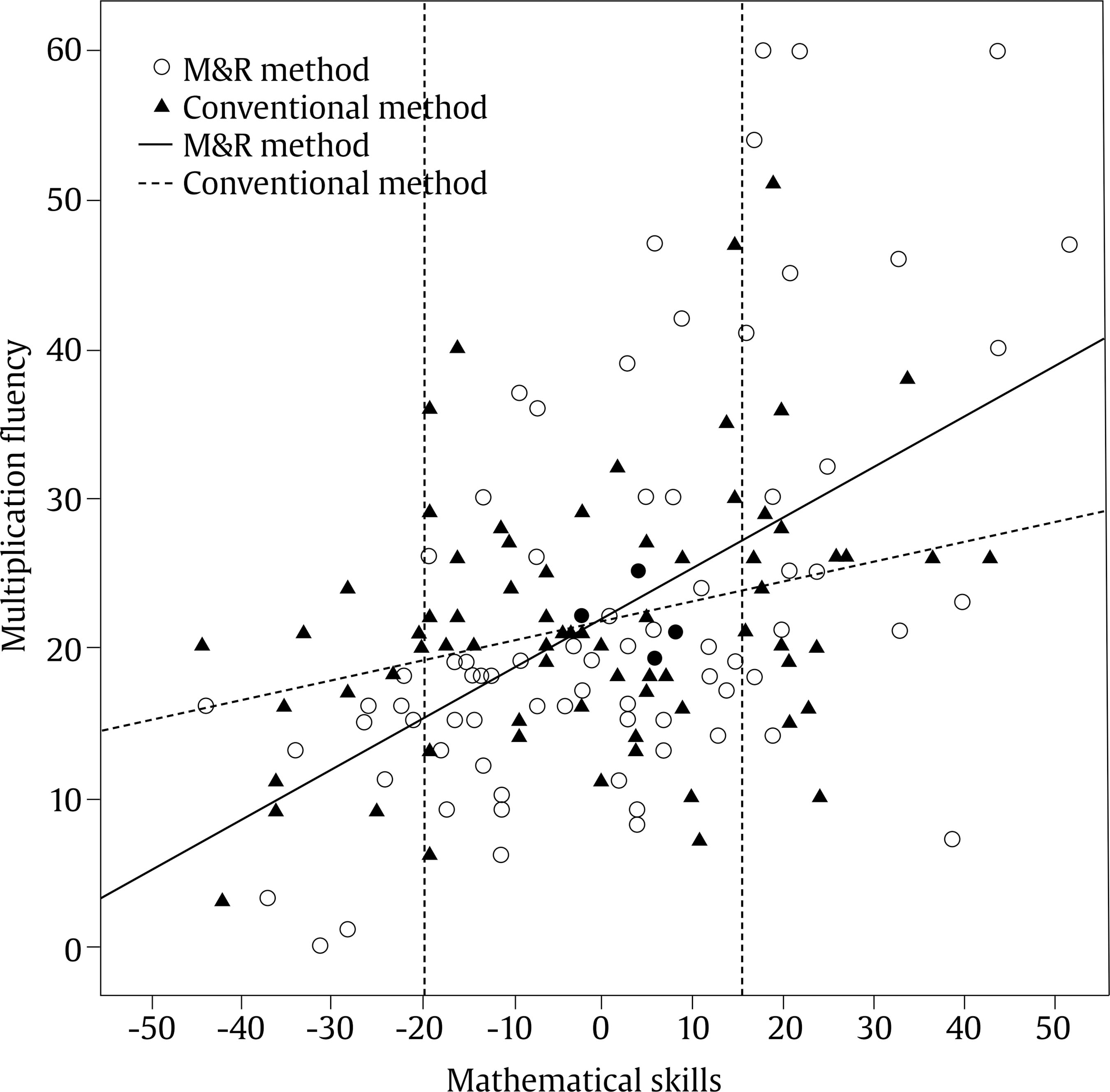

Table 3 includes the results from the moderation analysis. The model including the type of method, mathematical skills, and the interaction of both variables, significantly predicted the results in multiplication fluency: F(3, 156) = 17.74, MSE = 94.05, p < .001, R² = .25. No effects of type of curricular method on multiplication fluency (b₁ = -0.196, p = .89) was found, this reflecting there is not a lineal relationship between method and multiplication fluency at values of mathematical skills equals to 0. The effect of the moderator, mathematical skills level, was significant (b₂ = 0.259, p < .001), indicating that multiplication fluency increases with mathematical skills. More importantly, the interaction term indicated that the relation between the method type and multiplication fluency was moderated by children’s mathematical skills (b₃ = -0.229, p = .004).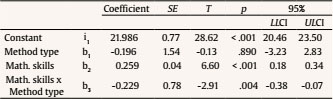

Using a Pick-a-Point approach, the interaction was analyzed by testing the effects of type of method at three levels of mathematical skills: one standard deviation below the mean, at the mean and one standard deviation above the mean (e.g., Hayes, 2013). The analysis (see Table 4) shows that the effect of type of method on multiplication fluency was statistically significant at one standard deviation below the mean, thus indicating that at this level of mathematical skills children in the conventional group scored higher in multiplication fluency than those in the M&R group. On the other hand, for values at one standard deviation above the mean, those in the M&R method outperformed those in the conventional method. Finally, no differences were observed in multiplication fluency between groups at the mean of mathematical skills.

A deeper analysis of this interaction with the Johnson-Neyman technique, that is, without categorizing a priori children in terms of mathematical skill levels, showed a difference between methods in favor of the conventional group for those participants with values of mathematical skills lower than -19.60 (15.6% of the sample). On the other hand, for participants with values of mathematical skills higher than +16.47 (22.5% of the sample), those in the M&R method showed higher multiplication fluency than those in the conventional method. No differences were found between methods for children with values of mathematical skills in the range -19.60 to 16.47 (see Figure 3).

Discussion

The present study has sought to compare the effectiveness of two curricular methods for learning multiplications. The M&R method, based on evidence and principles of cognitive and educational psychology, combines the use of memory and rules, the other, a conventional method, uses memory-based learning. An additional question was the role of individual differences in mathematical skills in terms of benefitting from these methods. Each method was followed in four classrooms over a six-month period as part of the math curriculum of second grade students. At the end of the school year, children were evaluated. Results indicate that the relationship between method and multiplication fluency was moderated by mathematical skills: a) among children with strong mathematical skills, those following the M&R method had achieved greater multiplication fluency; b) no difference was seen in children with intermediate levels of mathematical skills; and c) among children with poor mathematical skills, those following the conventional method scored better. In what follows we will discuss these results.

First, the analysis indicates simple effects of mathematical skills on multiplication fluency and no effects of method, although these results were qualified by an interaction between both variables, i.e., moderation. This moderation analysis showed the relevance of individual differences in terms of the advantages of one instructional method or the other, the relative benefits of the two methods being modulated by children’s mathematical skills. Against our predictions, children with poor mathematical skills attained greater fluency with the conventional method, whereas children with strong mathematical skills progressed more with the M&R method. In understanding these results, it may be useful to bear in mind that the M&R makes more demands on numerical and arithmetical understanding than the conventional method, which relies more on the memorization of the tables. It is perhaps not surprising, then, that students with strong mathematical skills benefitted more from a method based on conceptual understanding of rules and on memory than from one based almost exclusively on memory. Their knowledge of mathematics facilitated not only the understanding of the concepts and the single-step rules on which the method is based, but also of how to use these rules. Additionally, the time saved in learning problems through the use of rules can be employed in learning by memorization the smaller subset of multiplication facts that cannot be learned by rules. Our results here coincide with other research in the area of multiplication fluency intervention, which has found greater benefits for interventions based on understanding than for those simply based on memory. For instance, Brendefur et al. (2015) employed a form of instruction based on social-interactional and cognitive theories for five weeks, comparing this to one based on behavioristic techniques such as repetition and memorization. They found that the former led to increased multiplication fluency with a greater degree of consistency than the latter. Our data are in line with this, but also indicate that such a relationship is moderated by mathematical skills, as we found this only in the case of children with strong mathematical skills. Unexpectedly, we observed the reverse pattern in children with poor mathematical skills, in that those who followed the conventional method outperformed those that followed the M&R method. This is probably motivated by the higher demand on mathematical skills that the M&R method makes on children with poor mathematical skills. This method is based on achieving a proper understanding and effective use of the rules. Evidence suggests that for instruction to be productive it should include materials at an appropriate level of skill difficulty (Burns et al., 2006), and it seems that the M&R method did not do this for children with poor mathematical skills. On the contrary, children with poor mathematical skills who followed the conventional method gained greater fluency, this probably because they had a clearer understanding of what they were required to do (and how): memorize the multiplication tables. For children with poor mathematical skills, our results are in line with previous research and a meta-analysis that found that the multiplication fluency of children in the lower quartile for mathematics, or who experienced other learning difficulties, benefitted more from intervention methods based on drill and practice with modelling (Codding et al., 2011; Geary, 2004; Nelson et al., 2013), these being two components that form the basis of the conventional method.

One of the aims of the present study was to compare the relative effectiveness of the conventional and the M&R methods. There is no single finding here since, as we have noted, benefits depend on children’s mathematical skills. The M&R method was designed in light of earlier studies (e.g., Isaacs & Carroll, 1999; Miller et al., 1996; Woodward, 2006), and by taking into account evidence in the cognitive psychology literature on the detrimental role of interference (e.g., Campbell, 1995; De Visscher & Nöel, 2013, 2014a, 2014b, 2015; Geary, 2006; Kaufmann, et al., 2004) and the beneficial role, in terms of accuracy and speed, of single-step rules in mathematical achievement (Baroody, 1983, 1999; Ericsson et al., 1993; Uittenhove et al., 2016). Additionally, to reinforce the memory learning of a subset of multiplication problems, color cues and a portable time-tables were used. This should have been enough to promote better levels of multiplication fluency than the conventional group. And indeed, this was the case for the 22.5% of children with better mathematical skills. An additional positive characteristic of the M&R method is that efforts are constantly made to ensure the understanding of the rules. This is based on the idea that simply learning an algorithm (e.g., if a larger x smaller problem is given, just reverse it) is not as useful as understanding its conceptual basis. As previously noted, studies in the mathematical field have shown that conceptual instruction provides both understanding and better transfer to novel situations (e.g., see Rittle-Johnson & Alibali, 1999; Rittle-Johnson et al., 2001) and promotes students’ success and independence (Miller et al., 1996). Specifically, some data suggest that gains in fluency using memory procedures are not always accompanied by a flexible use of multiplications in other areas, such as problem solving (Brendefur et al., 2015; Geary et al., 2007; Woodward, 2006). On the contrary, it seems that intervention methods that use more conceptual approaches to learning facts, as the M&R does, increase not only fluency but also children’s ability to apply these skills to novel situations (e.g., Gray et al., 2000; Mulligan & Mitchelmore, 2009; Woodward, 2006). Thus, it seems reasonable to believe that the M&R method is better adapted to achieve this than the conventional approach, although we should make this claim with caution, given that our study did not measure children’s flexibility in the use of multiplication in different settings.

A direct implication of our results is that more time should be provided for understanding the rules when using the M&R method with children who have medium and poor mathematical skills. The worst observed effectiveness of this method with children with poor mathematical skills does not seem to be a consequence of incorrect design, but of incorrect implementation. A minimum level of mathematical skills is required in order to understand the rules, and indeed is a pre-requisite for running the method. The lack of specific mathematical skills may lead to a failure in understanding and in assuming the relevance of the rules and the logic behind the use of each strategy. So, when working with children with poor mathematical skills, the focus should be on increasing their mathematical knowledge prior to implementing methods that are based more on understanding than simply on memorization.

An important implication of our findings is the need to individualize instruction for students who present different mathematical skill levels, as suggested in previous studies (e.g., Connor et al., 2018; Morgan et al., 2015). Although this itself leads to certain complications, it seems that from the basis of a well-designed method, depending on the characteristics of the children, the method can be complemented in such a way that those with poor and medium mathematical skills are able to derive the same advantages that the M&R method provides for children with strong skills. Future implementation of this method with complementary material to promote understanding of the rules should yield evidence on its suitability to such children.

Certain limitations of this study might usefully be pointed out. First, as noted above, participants’ mathematical skill level used in the analysis was taken at the same time as the multiplication fluency task. Although it is expected that the measure of mathematical skills at the end of the application of the method would show a high correlation with the level of mathematical skill before starting the multiplication methods, a previous measure would allow us to establish a more causal relationship between mathematical skills and the effectiveness of the methods. In fact, the measure of mathematical skills in the M&R group taken one year before, that is, at the end of their first grade, showed a high correlation with the mathematical skills taken at the end of the application of the M&R method, rho =.516 (p < .001), thus the latter can be considered an acceptable proxy of the former. Similarly, the study may have benefitted from a broader measure of multiplication knowledge, not limited to fluency, and from testing the maintenance of the effects of the methods. This may have provided a better understanding of the differential benefits of the methods.

Additionally, it should be noted that since the M&R method is based on different psychological principles, our study cannot disentangle the relative role of each of these in the success of the intervention. As indicated in the Introduction, there are good reasons to expect that both reducing the number of facts to memorize and using color cues to code the problems can help students in encoding and retrieving the problems more effectively in their long-term-memory (e.g., Kaufmann & Pixner, 2012). Moreover, informal comments by both children and teachers suggests that using the portable multiplication table may have helped some students to see the learning of multiplications as a more attractive activity.

Finally, although the groups involved in the methods all belonged to the same school, it may be that the presence of different teachers and the non-random assignment of the students to the methods might have introduced some differences, and thus that students on the different methods may have differed in terms of mathematical knowledge, multiplication skills, or even in cognitive processes relevant for this learning (e.g., executive functions, working memory, phonology). Although this cannot be discounted, it should be borne in mind that no between-group differences were found in the measures of mathematical skills (see table 1). Additionally, an analysis of intraclass correlation (ICC) indicated that there were not high levels of correlation within each group, ICC= .37, Z-Wald = 1.45, p = .15, suggesting participants in both groups have similar characteristics. It is also a concern that our study has been carried out in a charter school, not a public school, and this could diminish the generalizability of our research. Although public schools are by far more frequent in Spain, 68%, charter schools are very common in Spain (28%), and more importantly, do not differ greatly in the type of children they receive and the educational practices they use (Eurostat, 2020). In support of this, according to the last PISA report, once the students’ socioeconomic level is considered, the differences in student’s performance between public, and charter and private schools disappear (OECD, 2019). So, with all due caution in this regard, it seems that, at least in Spain, our data may be generalized to students in other schools.

Several other issues in our study might also be highlighted with regard to previous work in the area. First, we implemented and compared teaching within curricular methods, not interventions. So, the methods were implemented as part of math lessons given by the children’s math teachers during the school term. In this sense our study is more ecological and might serve to guide teachers’ daily school activity (Star & Rittle-Johnson, 2016). It does not introduce foreign variables in the daily class activity in the way that most intervention studies do. However, the price to pay for being more ecological is having less experimental control, in that under these circumstances the random assignment of children to groups is not possible (see above). Second, an additional strength of the present study is that it analyzes the impact of these methods through looking at diversity, specifically by considering the fact that children differ in their overall mathematical skills. Third, by using a linear regression model, in this case moderation analysis, our study does not categorize children in terms of mathematical skills groups ad hoc, but by means of statistical criteria. This allowed for a more precise analysis of the data.

Conclusion

The present study has shown the differential benefits of two different methods of learning multiplication. A conventional memory-based method seems to be more efficient for children with poor mathematic skills, whereas a method based on understanding and using rules, and which limits the number of facts to be learned, seems more effective for children with stronger mathematical skills. Although these results should be taken with caution given the limitations of the current study, it seems that taking individual differences in mathematical skills into account appears to be a fundamental prerequisite of instructional methods as applied in the classroom for the learning of multiplication.