Validation of the Cooperative Learning Scale and Cooperation Global Factor Using Bifactor Structural Equation Modelling

Introduction

Cooperative learning has been around educational contexts for a long time, but it does not hold a uniform standpoint. Slavin (2014) identified four major theoretical perspectives on cooperative learning: a) motivationalist: task motivation is the most influential part of the learning process and task’s goal structure is the key element; b) social cohesion: students care about the group and help each other learn because they obtain benefits from group membership; c) cognitive-developmental: students must interact within developmentally appropriate tasks to increase their mastery of significant concepts and learn; and d) cognitive-elaboration: students must be involved in cognitive restructuring of new materials to learn.

Moreover, Johnson et al. (2013) believe that there are four types of cooperative learning: a) formal cooperative learning: the goal is to teach a specific content for a certain period of time (from one to several class periods); b) informal cooperative learning: the aim is to promote active cognitive processing of information and achieve a learning goal in provisional groups (from one task to one class period); c) cooperative base groups: the goal is to provide long-term, stable backing (in long-term, heterogeneous groups) to produce academic progress; and d) constructive controversy: the aim is to confront intellectual conflicts to obtain consensus between two individuals’ ideas, opinions, and solutions.

Regardless of the type of cooperative learning that is used in an educational context or the theoretical perspective that constitutes implementation foundation, there is agreement on the five basic elements that a cooperative learning framework must include (Johnson & Johnson, 2014): a) positive interdependence: all groupmates depend on each other to achieve the goal set, and everyone attains it if all of them do (everyone wins, no one loses); b) promotive interaction: all groupmates must be in direct contact to support each other while performing the tasks; c) individual accountability: each group member must be individually responsible for completing at least one part of the group’s task; d) group processing: the group must discuss and debate about the group’s work to assess its functioning; and e) interpersonal skills: as a result of the preceding elements, group members will develop interpersonal communication skills (i.e., cheer, praise, etc.), management skills (i.e., share, mediate...), and leadership skills (i.e., explain, suggest, etc.).

Several reviews and meta-analyses have provided enough evidence of the great success of cooperative leaning in promoting learning in the four different domains: cognitive (i.e., academic learning, decision making), social (i.e., interpersonal relations, empathy), affective (i.e., motivation, self-confidence), and physical (i.e., skills, motor performance). The works of researchers such as Gillies (2016), Johnson and Johnson (2002), or Roseth et al. (2008) have shown how beneficial it is for students to be placed in cooperative learning frameworks where teachers play an extremely important role promoting the needed interactions. These contexts have been found more productive on academic, personal, and social variables (i.e., achievement, self-esteem, perspective taking) than individualistic or competitive settings that, unfortunately, are very common in schools all over the world.

Moreover, cooperative learning has been considered “essential for meeting the four crucial challenges unique to the 21^st century” (Johnson & Johnson, 2014, p. 844): global interdependence, increasing number of democracies, the need for creative entrepreneurs, and changes in interpersonal relationships. These challenges are going to demand individuals capable of coping with stressful situations and contexts, and cooperative learning has been found to produce significant improvements in stress-coping and problem-solving skills among elementary school children, even after a life-threatening situation like a volcano disaster (Nopembri et al., 2019).

Despite the benefits of the implementation of cooperative learning programs in education, it is difficult for researchers and educators to find an adequate instrument to assess its implementation and/or its outcomes. More than 35 years ago, Johnson and Johnson (1983) developed the Classroom Life Management Questionnaire, which assesses global cooperative learning, positive interdependence, assessment, teacher academic support, or heterogeneity. Unfortunately, it does not include the five basic elements previously described. In Canada, the Centre for the Study of Learning and Performance (1998) developed the Cooperative Learning Implementation Questionnaire to understand the reasons why teachers implement, or not, this instructional approach. Later, Veenman et al. (2002) presented the Cooperative Learning Observational Schedule, which does include the five basic elements, but it was designed to be used by external observers and not the participating students. Later, Hijzen et al. (2006) developed two instruments: the Quality of Cooperative Learning and the Conditions for Cooperative Learning, the first assessing positive interdependence and interpersonal skills and the second evaluating teaching behavior and academic support tasks. Regrettably, some of the five basic elements are still missing. Finally, Bay and Çetin (2012) introduced the Cooperative Learning Process Scale and Fernandez-Rio et al. (2017) the Cooperative Learning Questionnaire. Both include all the basic elements, but they have been validated for non-English-speaking contexts. This brief review seems to indicate that there is a gap in the English Scientific literature on this topic. Researchers and scholars need adequate assessment instruments to fully investigate and/or implement cooperative learning in educational contexts.

Based on the aforementioned, the goals of the present study were two: a) to adapt and validate the existing Cooperative Learning Scale Spanish version for English-speaking Secondary Education contexts and b) to obtain a cooperation global factor. The instrument is designed to be used with students.

Method

Participants

A total of 778 students (378 boys, 391 girls), 12.77 ± 1.03 years (11-15 age range), enrolled in five different Secondary Education schools in Wales (year seven = 301, year eight = 276, year nine = 201) agreed to participate. Schools and students were included in the study because they had experienced cooperative learning in their classes prior to data collection. Regarding sample size, it depends on the matrix used for factor analysis, the number of items per factor, homogeneity of the sample, and especially items’ commonality (Lloret-Segura et al., 2014, p. 1157). Since there were three items per factor and the size of commonalities found, no fewer than 400 individuals would be the recommended. In the present study, this number has been substantially exceeded.

Instruments

Cooperative Learning Questionnaire. The original version of this instrument had been designed and validated for Spanish contexts (Fernandez-Rio et al., 2017). Following Muñiz et al. (2013), the International Test Commission Guidelines for test translation and adaptation were followed. They include 20 guidelines, grouped in six sections, and the vast majority were satisfied: 1) precondition: permission was obtained, laws were followed, best design was selected, test relevance was examined, and cultural differences were considered; 2) test development: cultural, psychological, and linguistic differences were observed, adequate design and procedures were used, instructions and content had meaning in the target population, format was also adequate, and a pilot study was conducted; 3) confirmation: the sample was defined, construct, method, and items were equivalent in the target population, and validity and reliability scores were obtained; 4) administration: it was adapted to the target population’ cultural and linguistic characteristics, and testing conditions were established; 5) score and interpretation: differences were interpreted based on demographic information, and scores were compared only at the level of invariance set; and 6) document: all information was provided for a correct use of adapted test. All items were translated into English by an officially certified translator, and then again into Spanish to test their similarity with original ones. In order to assess the English version’s content validity and applicability, it underwent a process of double debugging: a) experts trial: three professors belonging to different UK universities assessed item suitability, and b) pilot study: 50 secondary education students answered the questionnaire to modify and/or eliminate items difficult to understand and/or with errors. Based on their comments and to provide a smaller instrument, one item of each scale was removed. Finally, the English version included five factors with three items each: interpersonal skills, group processing, positive interdependence, promotive interaction, and individual accountability (Table 1). A five-point Likert scale response format was used (from one = totally disagree, to five = totally agree), because it is considered the best option for statistical reasons: it will reduce the frustration level of impatient respondents and increase response rate and response quality (Allen & Seaman, 2007). Moreover, the original version included this response format. Finally, a common stem was included: “In class…”. All the items are presented in Table 1.

Academic Self-Efficacy. Roeser et al.’s (1996) patterns of adaptive learning survey was used. It is a six-item, one-factor tool (i.e., “I can do even the hardest school work if I try”). Students responded on a 5-point Likert scale (from one = totally disagree, to five = totally agree). In our study, it obtained an adequate Cronbach’s alpha: .88 (95% CI [0.85, 0.93]).

Self-regulation. Pintrich and de Groot’s (1990) questionnaire was used to assess participants’ self-regulated learning. It is a one-factor scale with six items (i.e.,“ I ask myself questions to make sure I know the material I have been studying”). Participants answered on a 7-point Likert scale (from one = totally disagree, to seven = totally agree). In the present study, Cronbach’s alpha can be considered adequate, .79 (95% CI [0.76, 0.82]).

Procedure

First, permission was obtained from main researcher’s university Ethics Committee to conduct the study. Second, different schools, which have used cooperative learning in their classes, were contacted. Third, the whole project was explained to school administrators willing to participate, and permission was obtained from them and participating students. Fourth, in each participating school one teacher was in charge of data gathering. They all received precise instructions from the research team to conduct the process. An on-line version of the questionnaire was develop, using the Checklist for Reporting Results of Internet E-Surveys (CHERRIES; Eysenbach, 2004) to improve report quality. On a specific date, participating students were granted access to the on-line questionnaire. They were also granted confidentiality and anonymity, and asked to be totally honest.

Statistical Analysis

The goals of the present study were to: a) to adapt and validate the existing Cooperative Learning Scale Spanish version for English-speaking Secondary Education contexts and b) obtain a cooperation global factor. Several methods could be used to achieve both goals. One would be to examine high-order model factors, which test directly the hypothesis that the different factors can be combined into a high-order one. However, high-order factors models are highly dependent on restrictive conditions, which could be not valid in practice because they do not meet minimum requirements (Morin et al., 2016). A more flexible alternative to examine the presence of a cooperation global factor, that may underlie participants’ responses, would be to use a bi-factor representation, where all elements are used to define each respective subscale and to define a global factor (McAbee et al., 2014). A permanent concern in the present research was the multidimensionality of the scale in relation with the assessment of hierarchically arranged constructions (global cooperation factor). In the original validation of the instrument, a superior order factor model was used, which tests the hypothesis that several factors can be combined in a superior order single factor. However, these models are based on highly restrictive implicit assumptions that cannot be valid in practice and can explain why minimal proper fit requirements are not met at times (Reise, 2012). These models assume that the connection between items and the higher order factor are mediated by first order factors (McAbee et al., 2014), for the higher order factor not to explain by itself any variation beyond what has been already explained by the order factors. An alternative, flexible way of examining if the presence of a single “global cooperative learning” factor underlies responses to the questionnaire is the bifactor representation, where all the elements are used to define cooperative learning dimensions, but also to directly define a “global” factor. Morin et al.’s (2016) recommendations on the use of bifactor exploratory structural equation modelling (B-ESEM) and basic principles of model testing (Bollen, 1989) were followed. A priori B-ESEM representation with alternative models including one CFA or one ESEM, bifactor-CFA were contrasted. The two alternative models obtained are presented in Figure 1.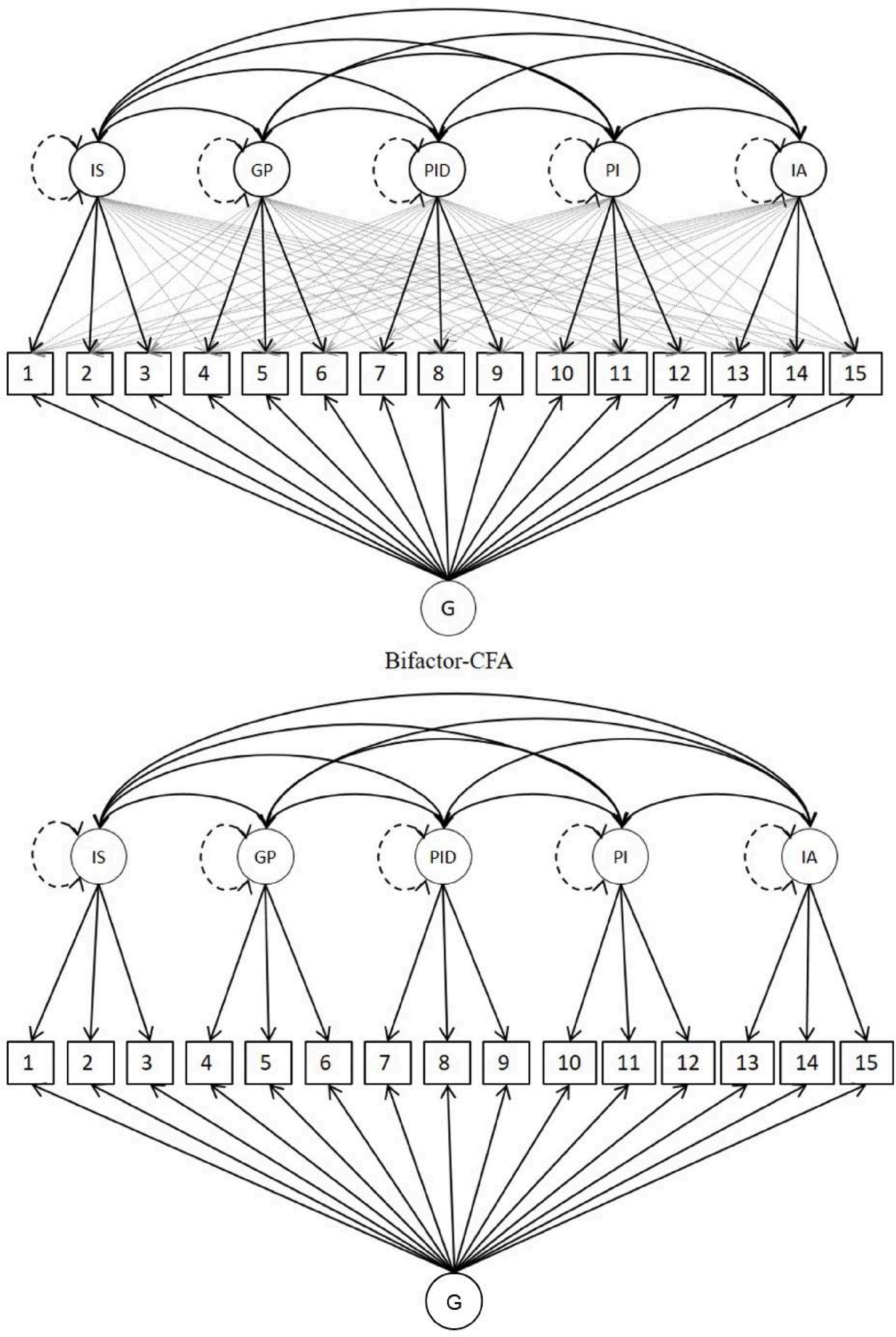

Estimation and Specification

All models were obtained using Mplus 7.3 (Muthén & Muthén, 2014) robust maximum likelihood (MLR) estimator. Confirmatory factor analysis (CFA) models were specified according to independent cluster model (ICM) assumptions, with items allowed to load onto their a priori cooperation factor, and all cross-loadings constrained to be zero. ESEM was specified using target rotation: item loadings on their a priori cooperation factors were freely estimated and all cross-loadings were also freely estimated but directed to be as close to 0 as possible. Bifactor-CFA (BCFA) models were specified as orthogonal, with each item specified as loading on the cooperation G-factor, as well as on their a priori S-factors corresponding to the five different cooperative learning dimensions. Finally, bifactor-ESEM (B-ESEM) was estimated using bifactor target rotation: all items were used to define the cooperation G-factor, while the five S-factors were defined using the same pattern of target and non-target loadings and cross-loadings as in the ESEM solution (Howard et al., 2018). The current models correspond to typical bifactor specifications where all items were used to define the G-factor, and one S-factor in line with theoretical expectations that all items reflect cooperative learning dimensions.

Model Comparisons

Two conditions were initially considered: the oversensitivity of the chi-square test of exact fit to the sample size and minor model misspecifications (Marsh et al., 2004). Therefore, model fit was assessed using goodness-of-fit indices: comparative fit index (CFI), Tucker-Lewis index (TLI), root mean square error of approximation (RMSEA) with confidence interval, and information criteria: Akaike information criteria (AIC), constant AIC (CAIC), Bayesian information criteria (BIC), and sample-size adjusted BIC (ABIC). Values larger than .90 and .95 for the CFI and TLI respectively and smaller than .08 or .06 for RMSEA indicate adequate fit to the data (Marsh et al., 2004). When comparing models, changes in RMSEA, CFI and TLI greater than .01 were considered significant (Chen, 2007). Information criteria (AIC, CAIC, BIC, ABIC) are considered useful to compare alternative models, with lower values indicating a better fitting model. These guidelines are recognized for confirmatory factor analysis and have been used in ESEM (Morin et al, 2016). Nevertheless, since ESEM includes more parameters than ICM-CFA (due to the free estimation of cross-loadings), Marsh et al. (2014) suggested that indicators including correction for parsimony (TLI, RMSAE, AIC, CAIC, BIC, ABIC) are extremely important to the assessment of model fit in ESEM.

Results

Measurement Models

Goodness-of-fit indices and information criteria associated with each of the estimated models is presented in Table 2. All models showed an adequate fit, but the ICM-CFA showed a better fit than B-CFA. The ESEM solution provided a better representation than the ICM-CFA based on lower information criteria scores and substantial improvement of the goodness-of-fit indices (ΔCFI = .015, ΔTLI = .013, ΔRMSEA = -.018). Finally, chi-square scores suggested that the B-ESEM model is the only one that provided a good fit.

Following Morin et al. (2016), ICM-CFA and ESEM models were compared, prior to moving to B-ESEM solution. Table 3 shows parameter estimates for ICM-CFA and ESEM (factor loadings, cross-loadings, and uniquenesses). Looking at loadings and cross-loadings, the overall size of the factor loading of items on their target factors was better in the ICM-CFA (λ = .63 to .82, M = .74) than in the ESEM (λ = .18 to .99, M = .60). However, both solutions showed well-defined factors corresponding to a priori expectations. In the ESEM solution, target factor loadings systematically remained higher than cross-loadings, which remained very small (| λ | = 0 to .35 M = .04). Only two cross-loadings were equal or higher that .30: item 2 of Promotive Interaction (“Group members interact with each other to complete the assignments”) cross-loaded on the Positive Interdependence factor at .30, and item 3 of Positive Interdependence (“The group needs the help of all its members”) cross-loaded on the Individual Accountability factor at .35.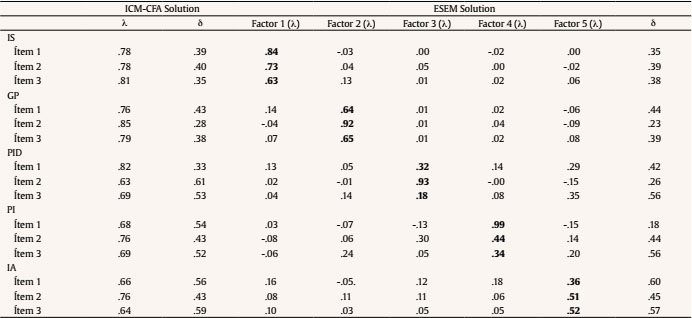

Table 4 shows that loadings of the B-ESEM solution were very similar to the observed in the B-CFA. Regarding the B-ESEM solution, it represented data quite well and provided an exact fit. A key advantage of the B-ESEM model, when compared to the ESEM, on top of its exact fit, is that it provides a single directly interpretable G-factor, in this study, a cooperation G-factor. Table 3 shows that results from the bifactor-ESEM solution revealed a well-defined G-factor, and this supports the idea of a cooperation global factor.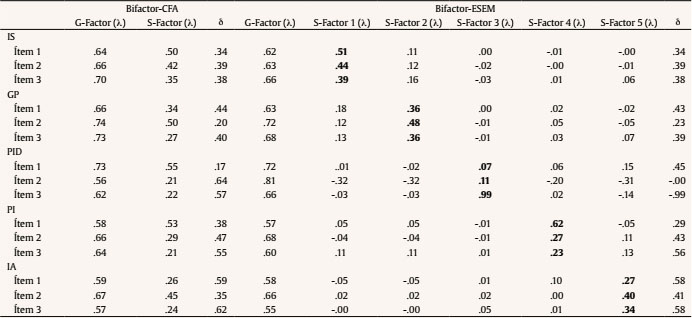

A more detailed examination of this solution revealed reasonably low cross-loadings, which remained lower than target loadings (| λ | <.18 to .33, M = .07), and well-defined S-factors (λ = .07 to .99, M = .39), with few exceptions. It is important to highlight that cross-loadings tended to be smaller in the bifactor-ESEM solution (than in ESEM solution), suggesting that part of the ESEM cross-loadings reflected the presence of factor G.

Predictive Models

From the final bifactor-ESEM solution, SEM analyses were used to assess the criterion-related validity of various cooperative learning factors. More precisely, these models were used to compare the added value of specific cooperative learning facets, above the G-factor (representing overall quantity of cooperative learning) in terms of percentages of explained variance in the various covariates considered. This comparison was conducted contrasting a model where only the G-factor was allowed to predict scores in covariates with a model where both G- and S-factors were allowed to predict scores in covariates. From the final bifactor-ESEM solution, SEM analyses were conducted to compare the added value of specific factors (which represent the quality of cooperative learning) beyond factor G (which represent global quantity) in terms of percentage of variance explained in the covariables considered. This comparison was obtained contrasting a model where only factor G could predict covariates’ scores, with a model where factors G and S could predict those scores. As shown in Table 5, when it is considered the only predictor of covariates, factor G was significantly associated, as expected, to higher scores in self-efficacy (explaining 38% of variance) and self-regulation (R² = 22%). All these connections were maintained in the next model, where S factors also were associated to covariates. This better model showed visible increases in the explained variance of both covariates: from 39% to 47% for self-efficacy, and from 20% to 29% for self-regulation.

Previous research has shown that traditional fit indices tend to favor bi-factor models (Morgan et al., 2015). Therefore, before concluding that the ESEM bifactor is the best, it is necessary to use specific indices that allow to assess general factor’s robustness and if the contribution of specific factors is relevant. Therefore, hierarchical omega and H coefficient, which evaluates each specific factor’s reliability (SF) controlling for the effect of the global factor (GF), are important to obtain. It is also advisable to calculate the explained common variance (ECV) and the percentage of uncontaminated correlations (PUC). Based on these ideas, MS Excel (IndicesBifactor.xls), which calculates all the previous indices, was built (Dominguez-Lara & Rodríguez, 2017; Rodriguez et al., 2016). Results showed a clear influence of the GF (ω = .884). PUC (.857) and ECV (.686) also showed a strong GF. The influence of the SFs, which showed the confinable variance of scores above the GF (Rodriguez et al., 2016), was: ω_is = .271, ω_gp = .209, ω_pid = .209, ω_pi = .208, and ω_ia = .176. H coefficients were: H_H.G = .923, H_H.is = .435, H_H.igp = .367, H_H.pid = .980, H_H.pi = .431, and H_H.ia = .286). They also showed that loading of SFs on items was not significant. Therefore, the interpretation of the three SFs independently would be too strict. Based on the aforementioned, both regarding exact fit to data and theoretical compliance to estimated parameters, the final model is the bifactor-ESEM model. This model also provides a simultaneous score to have all the cooperative learning factors joined, with a global estimation in only one predictive model (Howard et al., 2018).

Finally, Cronbach’s alphas for the Cooperative Learning Scale, its subscales, and the cooperation global factor were: interpersonal skills = .83 (95% CI [0.80, 0.85]), group processing = .84 (95% CI [.81, .87]), positive interdependence = .71 (95% CI [.6, .74]), promotive interaction = .75 (95% CI [.72, .78), and individual accountability = .72 (95% CI [.70, .75]), and cooperation global factor = .90 (95% CI [.86, .92]).

Discussion

The goals of the present study were two: a) to adapt and validate the existing Cooperative Learning Scale Spanish version for English-speaking Secondary Education contexts and b) to obtain a cooperation global factor. Results showed that the two goals have been reached.

Regarding the first goal, to adapt and validate the existing Spanish version of the Cooperative Learning Scale for English-speaking Secondary Education contexts, results showed that it is a valid instrument. The use of a relatively novel bifactor exploratory structural equation modelling (B-ESEM) to identify multidimensional relevant sources present in complex psychological measures like the one under study was fundamental. Results from the ESEM solution showed well-defined factors corresponding to a priori expectations. It should be noted that, unfortunately, not all specific (group) factors have enough entity (i.e., PID and PI have two items with a factor loading very small). These items seem to be explained by the general factor. Based on an already solid instrument validated for Spanish-speaking educational contexts (Fernandez-Rio et al., 2017), all fit indices and information criteria showed that the Cooperative Learning Scale was a valid instrument for English-speaking settings. A second advantage of this scale, besides language, was that it is the first one to include the five basic elements of cooperative learning. All previous instruments (Centre for the Study of Learning and Performance, 1998; Hijzen et al., 2006; Johnson & Johnson, 1983; Veenman et al., 2002) had the same deficit: they did not include all of them. The final advantage of the newly validated instrument, which is a significant improvement over its precedent (Fernandez-Rio et al., 2017), was that the new one has only three items in each factor (the other one had four). This is very important because researchers and scholars seek assessment instruments easy to use. Based on these three positive ideas, the Cooperative Learning Scale could be considered a step forward in the scientific literature on cooperative learning assessment.

Regarding the second goal, to obtain a cooperation global factor, results showed that the Cooperative Learning Scale can produce it. The bifactor exploratory structural equation modelling (B-ESEM) revealed a well-defined G-factor, which supported the idea of a cooperation global factor. To the best of our knowledge, this is the only assessment instrument that provides this type of element. None of the previously validated tools (Bay & Çetin, 2012; Fernandez-Rio et al., 2017; Hijzen et al., 2006; Johnson & Johnson, 1983; Veenman et al., 2002) identified and provided a cooperation factor. This is very important because it provides researchers and scholars with another instrument to assess cooperative learning and enables them to compare different implementations and/or groups of students. Again, this could be considered a step forward in the scientific literature on cooperative learning assessment, because it is the first time that a cooperation global factor, similar to other measures like the self-determination index (SDI; Vallerand et al., 1997), is introduced.

In conclusion, methodologically, this study has shown the use of an original bifactor exploratory structural equation modelling (B-ESEM) to identify multidimensional relevant sources present in complex psychological measures like the assessment instrument under study. Functionally, the Cooperative Learning Scale has proven to be a valid instrument to assess cooperative learning in English-speaking contexts, including its five basic elements and a cooperation global factor.