Quasi-ipsative Forced-Choice Personality Inventories and the Control of Faking: The Biasing Effects of Transient Error

Introduction

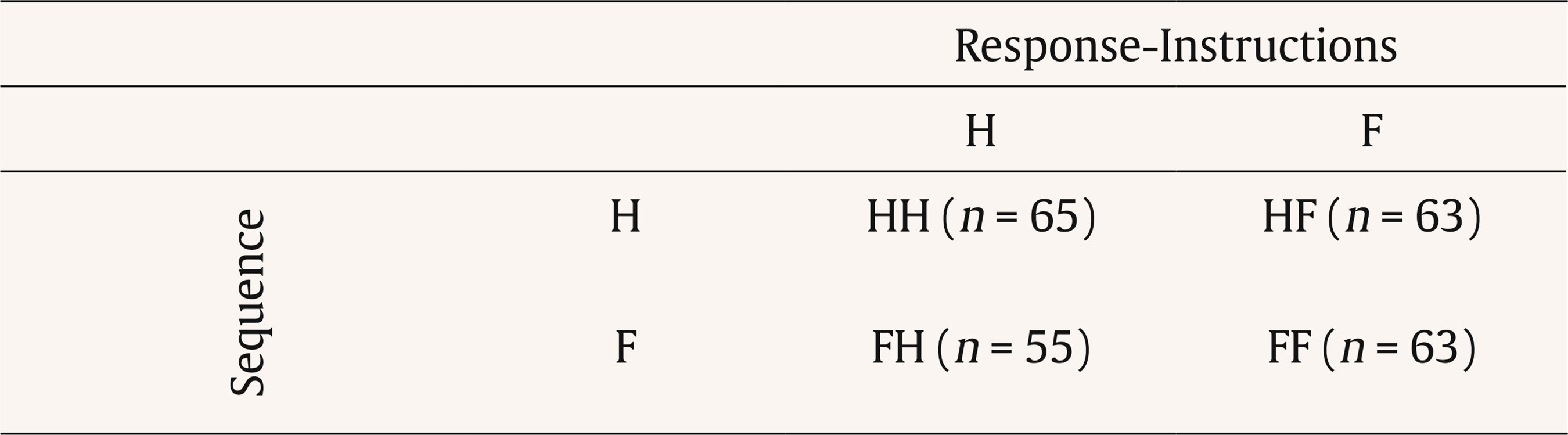
Faking is one of the most pervasive phenomena in work and organizational psychology (W/O) and, particularly, in the personnel selection area. For instance, empirical findings have shown that applicants can fake their responses to personality measures (e.g., the Big Five) when they are involved in an assessment process (such as personnel selection, work promotions processes, or academic decisions) increasing or decreasing their actual scores on these measures (Martínez, 2019; Martínez et al., 2021a, 2021b; Martínez & Salgado, 2021; Morgeson et al., 2007; Murphy, 2005; Salgado, 2016; Zickar & Gibby, 2006). Consequently, this behavior may have serious consequences for hiring and organizational decision-making because the quality of the decisions may be questionable (see, for instance, Donovan et al., 2014; Griffith et al., 2007; Martínez, 2019; Morgeson et al., 2007; Salgado, 2016). The effects of faking do not affect personality inventories only, but also other assessment tools such as personnel interviews, biodata, and integrity tests, to mention but a few examples. Furthermore, this is a widespread phenomenon as anyone could commit faking, and any organization that uses personality inventories could have their selection processes affected by faking (Griffith & Converse, 2012). For these reasons, a major concern in applied personality measurement contexts (e.g., personnel selection) is to, firstly, know the extent to which personality scores are affected by faking and, secondly, to develop instruments, methods and assessment strategies that permit us to control and reduce the effects of faking. This paper aims to shed further light on these issues.

With regard to the first concern, the extent of faking in personality scores over the years, many studies have been carried out to estimate the effects of faking on personality inventories. Those studies have shown that faking has significant negative consequences on the psychometric properties of personality inventories (Salgado, 2016). For instance, faking increases the mean and decreases the standard deviation (SD) of the score distribution of personality variables. In addition, faking also produces a decrease in reliability and criterion validity and can modify the factor structure of personality inventories (e.g., Birkeland et al., 2006; Douglas et al., 1996; Hooper, 2007; Hough et al., 1990; Martínez et al., 2021a, 2021b; Salgado, 2016; Salgado & Lado, 2018; Viswesvaran & Ones, 1999).

Typically, research has examined the effects of faking by comparing the scores under two conditions: (a) responding under honest instructions and (b) responding following faking instructions (see, for instance, Cao & Drasgow, 2019; Martínez & Salgado, 2021; Mesmer-Magnus & Viswesvaran, 2006; Salgado & Lado, 2018; Viswesvaran & Ones, 1999). Typically, these two sets of scores are obtained within a single group of participants (within-subject design) or with two independent groups of participants (between-subject design). To the best of our knowledge, all the studies, both correlational and experimental, that have examined the effects of faking on personality inventories adopted one of these two designs. Nevertheless, they have some methodological limitations that might contribute to the overestimation or underestimation of the extent of faking, as they do not control some sources of variance that may be affecting the measurements (e.g., idiosyncratic variations or transient variations). Despite these design limitations, to date, no studies have been conducted with other experimental designs that might control for these sources of error.

Regarding the second above-mentioned concern, i.e., how to control and reduce faking, several assessment methods have emerged over the years with different degrees of effectiveness in their capacity to control and reduce faking. Among them, recent empirical evidence has shown that forced-choice (FC) personality inventories stand out as methods capable of reducing the effects of faking on personality measures (see, for instance, Converse et al., 2006; Dilchert & Ones, 2012; MacCann et al., 2012; Morillo et al., 2019; Salgado, 2017; Salgado & Lado, 2018). Typically, FC personality inventories require that individuals choose between response options with the same or very similar degrees of social desirability. This characteristic makes it more difficult for candidates to voluntarily distort their responses.

Hence, the aim of this research is to contribute to the study of the effects of faking on FC personality measures using an experimental design never applied to date in the study of faking behavior, the Latin-square experimental design. The Latin-square design (LSD) is a type of experimental design that consists of randomly assigning subjects to different instructional sets created with the aim of controlling several sources of variance in order to know, in a more specific way, the effects of a concrete phenomenon on the relationship between two variables (Cochran & Cox, 1978; Kirk, 2013). In the next sections, we discuss the concept and effects of faking, we point out the characteristics of the various FC personality methods and their faking resistance, we review the literature on the experimental designs used to estimate the effects of faking, and we introduce the LSD as a better method for estimating the true effect of faking on personality scores.

Concept and Effects of Faking

Faking can be described as a type of response bias wherein individuals voluntarily distort their responses to non-cognitive instruments (e.g., personality tests, interviews, biodata, etc.) trying to give a portrait of themselves that provides them some benefit or advantage in the assessment processes (e.g., Birkeland et al., 2006; Donovan et al., 2014; García-Izquierdo et al., 2020; Griffith & Converse, 2012; Salgado, 2016). As noted by Ziegler et al. (2012), faking occurs when there is a perception on the part of the subject that there is an imbalance between the situational demands and his/her individual characteristics.

In this regard, numerous studies that have shown that faking can severely and negatively affect some selection instruments, particularly the single-stimulus (SS) personality inventories (e.g., NEO-PI-R, MMPI-II, California Personality Inventory, Hogan Personality Inventory, 16PF-V), perhaps the most commonly personality instruments used to make hiring decisions (Rothstein & Goffin, 2006). A main characteristic of SS personality inventories is that every statement must be rated in to describe individual personality (for instance, using Likert scale, yes/no, or true/false answer format). Many researchers and practitioners were (and are) concerned with the potential sensitivity of SS to be faked when hiring decisions are to be taken (see Christiansen et al., 2005; Murphy, 2005).

Recently, Salgado (2016) proposed a theoretical account to explain the psychometric effects of faking. According to this theory, faking is a source of error variance that produces two simultaneous artifactual effects: increases the mean and reduces the standard deviation of the distributions. In other words, faking produces an artificial homogenization of the samples reducing the range of scores obtained by the individuals. Also, this causes that the individuals seem more similar to each other than they really are (due to the restriction of the range of scores). Likewise, these artifactual effects produce a reduction in the reliability and predictive validity of personality instruments and affect the factorial structure (construct validity) of the SS measures. Accordingly, faking would have a direct consequence on the selection processes: applicants that commit faking would be undeservedly in higher ranking positions than those applicants who have not faked. Consequently, the evaluators could make wrong hiring decisions during assessment processes (Griffith et al., 2007; Komar et al., 2008; Salgado, 2016).

Empirical findings have shown that the main effect of faking on SS inventories was an artificial increase of the mean, a reduction in the standard deviations of the scores, and the lowering of the reliability coefficients (Salgado, 2016). These results have also been supported by the meta-analysis of Viswesvaran and Ones (1999) in experimental settings, and by the meta-analyses of Birkeland et al., (2006), Hooper (2007), and Salgado (2016) in occupational settings, where they compared real job applicants’ samples and non-applicants’ samples (i.e., incumbents or respondents in a non-selection setting). Empirical evidence concluded, therefore, that individuals can and do distort their scores on SS instruments if they are motivated to fake.

Accordingly, it was suggested that forced-choice (FC) personality inventories might be a robust alternative procedure to SS personality inventories in order to cope with the effects of faking in practical assessment contexts (e.g., Cao & Drasgow, 2019; Fisher et al., 2019; Martínez, 2019; Martínez & Salgado, 2021; Morgeson et al., 2007; Salgado & Táuriz, 2014).

Forced-Choice Personality Inventories

In the last few years, FC personality inventories have been recommended as measures that might better control the effects of faking than SS tests do (Adair, 2014; Cao & Drasgow, 2019; Martínez et al., 2021a, 2021b; Martínez & Salgado, 2021). FC personality inventories are characterized by presenting sets of items (usually, the options are grouped in pairs, triads, or tetrads) that have the same degree of social desirability (see, for instance, Baron, 1996; Bartram, 1996; Cao & Drasgow, 2019; Salgado & Táuriz, 2014). Respondents must choose the alternative that best describes them and, in some cases, the alternative that worst describes them. Given that the answer options are similar in their level of social desirability, it will be more difficult for the participants to distort their responses. Consequently, the use of FC personality inventories might reduce the effects of faking (Brown & Maydeu-Olivares, 2013; Christiansen et al., 2005; Converse et al., 2006; Dilchert & Ones, 2012; Jackson et al., 2000; Martínez, 2019; Martínez & Salgado, 2021; Morillo et al., 2019; Salgado, 2017; Salgado & Lado, 2018).

Typically, three types of FC scores (i.e., normative, ipsative, and quasi-ipsative) are distinguished depending on how the answer-choice is made, each of them with specific psychometric characteristics (see Abad et al., 2022; Clemans, 1966; Hicks, 1970; Meade, 2004; Salgado et al., 2015; Salgado & Táuriz, 2014). Normative FC scores present unidimensional items, each item being a scale that just evaluates one personality factor. So, the normative scores allow for the analysis of the results on an inter-individual level. In the case of ipsative FC scores, all the alternatives presented in each item are scored by the respondents. Therefore, there is dependence in the scores between factors, that is, the score for each dimension depends on an individual’s scores on the other graded dimensions. Consequently, the sum of the scores obtained for each individual is a constant, and ipsative scores only allow intra-individual comparisons. The third FC scores, the quasi-ipsative ones, do not meet all the criteria of pure ipsative scores but present some characteristics associated with them (Clemans, 1966). Specifically, a score is quasi-ipsative when it presents the following characteristics (Hicks, 1970; Horn, 1971; Salgado & Táuriz, 2014): (1) the results for each factor vary between the individuals over a certain range of scores, (2) even though these inventories have some properties in common with the ipsative FC, the scores do not add up to the same constant for all individuals, (3) the increase in the score on one personality factor does not necessarily produce a decrease in the other factors. In fact, we can distinguish two types of quasi-ipsative FC scores (Horn, 1971): (1) quasi-ipsative, algebraically-dependent scores, which show some degree of ipsativization of scores or, in other words, a metric dependence exists between the scores, and (2) quasi-ipsative, non-algebraically-dependent scores, where the score for each personality factor is not influenced by the score in other personality dimensions.

Empirical evidence has shown that FC inventories show an important degree of faking resistance. For instance, the meta-analyses of Adair (2014), Cao and Drasgow (2019), and Martínez and Salgado (2021) have shown that, compared with the SS personality inventories, the three types of FC personality inventories reduce the effects of faking on personality scores, both in experimental studies and in real personnel selection contexts. In particular, the quasi-ipsative FC inventories stand out from the other two formats in faking-control effectiveness, as the effects sizes found were smaller than those found for normative and ipsative scores (Martínez & Salgado, 2021).

Experimental Designs for Estimating the Effects of Faking

Despite extensive research on faking, a matter of debate is how faking should be estimated and/or measured. The difficulties encountered when evaluating this construct are largely due to its intrinsic nature and the diverse set of behaviors that it comprises, but also the different methods used to estimate it (Ellingson et al., 2007; Martínez, 2019; Ones et al., 1996; Viswesvaran & Ones, 1999). Different methods have been applied to quantify the degree of faking, for instance, social desirability scales or the application of confidence intervals.

The most widely used method to examine the effects of faking are experimental studies that allow comparisons among the scores obtained both under honest and under faking instructions conditions (Mesmer-Magnus & Viswesvaran, 2006; Smith & McDaniel, 2012; Viswesvaran & Ones, 1999). This strategy can be carried out by combining two types of characteristics: (a) the research context and (b) the type of design used.

In relation to the research context, two types of studies can be distinguished: (1) correlational studies (i.e., studies in real contexts) and (2) experimental studies (i.e., lab studies). In personnel selection, the first type of studies refers to the comparison between actual job applicant samples and incumbent samples. This perspective assumes that applicants are motivated to fake but that incumbents are not motivated to voluntarily modify their answers. Therefore, the differences between applicants and incumbents would indicate whether or not faking has been committed (see Mesmer-Magnus & Viswesvaran, 2006). This method can be considered an indicator of typical performance on the test, that is, differences that occur naturally in a real personnel selection context. However, given the difficulties involved in obtaining equivalent samples of applicants and incumbents, most studies are carried out in experimental contexts in which selection processes are simulated.

In experimental settings, two different strategies have been used until now. In the first strategy, participants are randomly assigned to a fake good response-condition (equivalent to the role of applicants) and to an honest response-condition (equivalent to the role of incumbents) before responding to the tests. In the fake good response-condition, the participants are instructed to answer the test by trying to show an improved (“the best”) image of themselves. In the honest response-condition, they are instructed to be totally honest and candid when answering the tests. In those cases, the experimental design is a between-subject one. The second strategy requires the participants to take the personality inventory twice, first in one condition (e.g., under honest-response instructions) and next in the second condition (e.g., under faking-response instructions). The comparison between the scores in both conditions would produce an estimate of faking. In those cases, the experimental design is a within-subject one.

In experimental settings, it is considered that the results reflect the effects of faking in contexts of maximum performance in which it is clearly intended to find the greatest difference between both experimental conditions.

Salgado (2016) carried out a meta-analytic review of the effects of faking in which the two scenarios were considered (i.e., real contexts and lab contexts). The results pointed out that faking estimates obtained in a real context (i.e., applicants vs. incumbents) and faking estimates obtained via an experimental design produce very similar effect sizes. This finding has an important implication for empirical research since it can be assumed that the results found in experimental studies have the same accuracy as those found in real contexts.

In examining the consequences on faking estimates of using one design type or the other, on the one hand, within-subject designs allow us to compare the individual differences that can occur within the same group under different conditions (see Viswesvaran & Ones, 1999). However, this methodology is not without limitations. The most prominent one is the suggestion that the results may be affected by the subject’s pretest experience (remember that they complete the same test twice), as well as by the personal characteristics of each individual evaluated (Cook & Campbell, 1979; Mesmer-Magnus & Viswesvaran, 2006; Viswesvaran & Ones, 1999). On the other hand, between-subject designs are carried out with two independent samples; therefore, the main criticism of between-subject designs is that it is assumed that the effect of faking will be the same for all subjects even though only a part of the sample responds under faking-responding instructions and the other part responds under honest-responding instructions.

An issue that arises about these two types of designs is whether equally accurate results are obtained regardless of which of them is applied. Viswesvaran and Ones (1999) studied the incidence of faking in personality measures using both designs and compared the resulting estimators in each one. They concluded that within-subject designs are much more accurate in explaining the effects of faking. They assumed that the within-subject designs have greater statistical power by allowing the two groups to be fully equated. However, both are typical “before-after” designs (designs where we only obtain one answer under each condition) and some researchers have pointed out that this type of design does not control some sources of variance, particularly transient measurement error, whose effects could be misassigned to faking (Heggestad et al., 2006; Martínez, 2019). Consequently, other experimental strategies that control these sources of error, like for instance Latin-square designs (LSD), should be applied to get a more accurate estimate of faking effects (Kirk, 2013).

Latin Square Design as an Alternative Design for Studying Faking

LSD is a type of experimental design with repeated measures that is appropriate to use when it is necessary to control two sources of variability, i.e., error due to the treatment (faking) and transient errors. In LSD, the number of levels of the main factor (faking/honest behavior in our case) must coincide with the number of levels of the secondary factor (for instance, the order of the instructions). Also, it must be assumed that there is no interaction between any pair of variables (Cochran & Cox, 1978; Kirk, 2013).

Let K be the number of levels of each of the factors, then LSD uses K² blocks and each of these blocks corresponds to one of the possible level combinations of the two control variables. In each block, a single experimental condition is applied so that each experimental condition must appear with each of the levels of the two control variables (see Gao, 2005; Grant, 1948; Kirk, 2013). That is, if we consider a table where the rows and columns represent each of the two-block variables and the cells the levels of the main variable, this means that each variable must appear once in each row and in each column (see Figure 1).

Therefore, the sample in an LSD is divided in several independent experimental groups, each of which is single “evidence” of the combinations of variables. Furthermore, as the combination of variables is assigned randomly in each experimental group, systematic biases are avoided. In other words, LSD allows us to isolate the differences between the samples and experimental and environmental conditions (Cochran & Cox, 1978; Grant, 1948; Kirk, 2013).

In summary, LSD can be more informative on the effect of the main variable studied (i.e., faking behavior in our case), but it will be also more informative about the differences observed in the samples due to the individual and contextual characteristics (e.g., transient error). Therefore, from a methodological viewpoint, using an LSD will permit us to better examine the effects of faking on FC personality inventories and to obtain a more accurate estimate of faking effect size.

Aims of the Study and Research Hypothesis

The current study aims to contribute to the knowledge on faking in FC personality measures by using an experimental design never applied to date in the study of the faking effects, the LSD. Specifically, the main objective is to know the amount of faking in a Big Five FC quasi-ipsative personality inventory, after controlling for the two main sources of variability that may be affecting the results, i.e., honest vs. faking behavior and transient error. Therefore, with this design, we aim to isolate the differences between the samples that are because of faking from those that are due to individual or environmental differences (i.e., transient measurement error).

Based on the previous above cited theoretical and empirical evidence, we state the following hypotheses.

Hypothesis 1: Faking produces an increase in the mean and a reduction in the standard deviation of the scores of the personality factors.

Hypothesis 2: Quasi-ipsative FC personality inventories show smaller observed faking effect as compared with the one found for SS personality inventories revealed in previous meta-analyses (e.g., Birkeland et al., 2004; Viswesvaran & Ones, 1999; Salgado, 2016).

Hypothesis 3: The transient error in personality scores accounts for a significant percentage of the observed faking effect size.

Hypothesis 4: When the effects of transient error on personality scores are discounted, the magnitude of the faking effect size in a Big Five FC personality inventory is very small on average (d < 0.10).

Method

Sample

The sample was composed of 246 undergraduates from a Spanish university; 65.85% of the sample were women (n = 162) and 34.15% were men (n = 84). All of them were first-year students. The average age was 19.70 years old (SD = 3.73). Participation in this experimental study was voluntary. Small face-to-face groups were organized to answer the tests. The subjects provided informed consent to participate in the study.

Measures

Quasi-ipsative Personality Inventory (QI5F_tri; Salgado, 2014)

The QI5F_tri is a quasi-ipsative forced-choice personality inventory designed to assess the Big Five personality factors. The test consists of 140 triads that evaluate the Big Five (each factor is assessed by 28 triads). In each triad, individuals are required to indicate which option best describes them and which option worst describes them. An example of a triad is: “I am a person who is (a) altruistic (agreeableness), (b) perfectionist (conscientiousness), (c) very imaginative (openness to experience)”. The QI5F_tri personality inventory provides a score for each factor that is algebraically non-dependent from the score on the other factors, that is, it implements Horn’s strategy: the items used to evaluate a dimension are not used to evaluate other dimensions. Consequently, the factors are algebraically non-dependent even though the nature of the score is quasi-ipsative (Horn, 1971; Salgado, 2014; Salgado & Lado, 2018). The internal consistency coefficients (McDonald’s ω) were .74, .77, .86, .72, and .81, and .87, .83, .93, .85, and .89 (great lower bound; GLB) for emotional stability (ES), extraversion (EX), openness to experience (OE), agreeableness (A), and conscientiousness (C), respectively (Salgado, 2014). Test-retest reliabilities ranged from .72 for agreeableness to .86 for openness to experience (Salgado, 2014). In the present sample, test-retest reliabilities were ,82, .83, ,83, .78, and .84, for ES, EX, OE, A and C, respectively. Evidence of the convergent validity of the QI5F_tri using an SS personality inventory was reported by Otero et al. (2020) and Martínez et al. (2021a; 2021b).

Experimental Design and Procedure

To carry out this study, we used a 2 x 2 Latin-square experimental design (LSD) with repeated measures. The participants answered the personality questionnaire twice at two different times. Therefore, data collection was performed in two sessions with each group, leaving a time interval between each of the sessions of between 2 and 3 weeks. In each session, participants were randomly assigned to one of two experimental conditions (honest or faking), so that from the combination of the experimental conditions and the number of sessions the participants were included in one of the following four experimental groups (instructional sets): honest-honest (H-H), honest-faking (H-F), faking-honest (F-H), and faking-faking (F-F) (see Figure 2).

A random number table was used to randomize participants for each response condition in each session. Specifically, a number was assigned to each participant, which had previously been randomly associated with an experimental condition.

Regarding the instructions to answer the QI5F-tri personality inventory, for the honest condition, the participants received the following instructions provided by the instrument:

In this questionnaire you will be presented with sets of phrases grouped into triads. Try to rank them by first identifying the one that best describes you, the one that second best describes you, and finally the one that describes you least. In each item, mark a plus sign (+) next to the phrase that best describes you and a minus sign (-) next to the phrase that least describes you. You should leave blank the one you considered second.

For the faking condition, the instructions were modified in such a way that participants were encouraged to fake. The following paragraph was added to the above instructions:

When answering, assume that you are in the last step of a selection process for a very attractive job. Since it offers you a great opportunity to advance your professional career, you want to get that job. To do this, you must answer the test trying to give a better image of yourself.

In both response conditions the inventory was administrated using the Google Forms application and the participants only had access to the test during the time they attended the study. Due to confidentiality reasons, the data set is only available from the first author upon a reasonable request.

Results

Table 1 reports the descriptive statistics for the Big Five in each experimental group. Taken together, the means and the standard deviations obtained for all groups and experimental conditions are very similar. There are no big differences in the values for all experimental conditions, though we can appreciate slight variations in the results across groups. For instance, comparing the results for the H-H condition (M = 23.45~29.63) with the results for the F-F condition (M = 22.46~30.10) it can be observed that there is some degree of variability in the magnitude of the mean and standard deviation values, even though the participants answered both times under the same response-instructions. These differences were more noticeable between the honest and faking response-conditions in the groups in which the participants answered the inventory under both instructional sets. Specifically, the mean ranged from 22.57 to 31.75 in the H-F response-conditions and from 21.51 to 30.39 in F-H instructions. In particular, the results showed that the means are slightly higher under faking response-conditions than under honest response-conditions and that the values of the standard deviations are smaller under faking instructions compared to the values under honest response-conditions. These findings supported Hypothesis 1.

T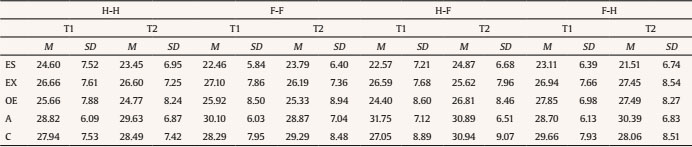he results also showed that there is some degree of variability in the means when the participants respond under the same experimental instructional sets (i.e., H-H and F-F). Clearly, this fact indicates that transient measurement error is present in estimated observed faking as predicted by Hypothesis 2.

In order to estimate the effect size for the transient error, we used the formulas developed by Dunlap et al. (1996) to estimate d coefficient. Dunlap et al.’s formulas for d allow for a more accurate estimate of effect size than the conventional Cohen’s d formula, as they take into account the correlation between matched groups. This means that these formulas control to a greater extent the inside design variability. The results obtained are reported in Table 2.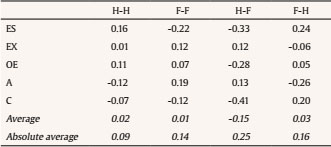

As can be seen, the d values ranged from -0.12 to 0.16 when comparing the values among H-H conditions. The d values ranged from -0.22 to 0.19 for comparisons among F-F conditions. The absolute (i.e., sign ignored) average d value was 0.09 for the H-H condition and it was 0.14 for the F-F condition. Therefore, these results showed that there was variability in the response of the participants even when the participants answered the personality inventory under the same response-instructions both times. Thus, transient error showed a small but relevant effect size in the stability of participants’ personality scores under both honest and faking instructional sets.

In the H-F experimental condition, the values of d ranged from -0.41 to 0.13, with an absolute average d of 0.25. Lastly, the values of d ranged from -0.26 to 0.24 for the F-H experimental condition, with an absolute d average of 0.16. Pooling the two sets of estimates, the absolute average d is 0.21 for the comparison between honest and faking instructional sets.

Regarding the effect of faking on personality scores, the first column of Table 3 reports the degree of observed faking for the Big Five (average of d estimates of H-F and F-H conditions, sign reversed). The results show d coefficients that can be considered moderately small for conscientiousness and emotional stability (0.31 and 0.29, respectively) to small or very small for agreeableness, openness to experience, and extraversion (0.20, 0.17, and 0.09, respectively). These findings indicate that the quasi-ipsative FC format of the current personality inventory is very robust against the faking effects, if we compared these estimates with those reported in previous meta-analyses for the SS personality inventories. For instance, Viswesvaran and Ones (1999) reported d values ranging from 0.47 to 0.93 (average d = 0.66). Therefore, the current d estimates are remarkably smaller than those previous estimates which supports Hypothesis 2. Also, the observed estimates of faking effects found in this study concur with the findings of Cao and Drasgow (2019) and Martínez and Salgado (2021) for the quasi-ipsative FC.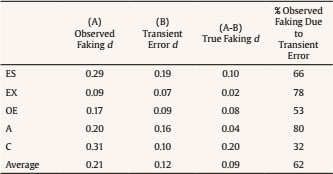

The second column of Table 3 reports the effect size for the transient error in the personality scores under the same instructional set (average of d estimates of H-H and F-F conditions, sign reversed). The results show d coefficients ranging from 0.07 to 0.19, with an average d of 0.12.

The third column of Table 3 reports the effect sizes of true faking for the Big Five. We label “true faking” the faking estimate obtained when the effect size of transient error is discounted from the observed faking effect size. As can be seen, true faking effect sizes are small or very small, ranging from 0.02 to 0.20, with an average size of 0.09. This finding means that the effect of faking on the personality scores obtained with a quasi-ipsative FC inventory are of almost no practical importance when the effect of transient error is discounted. The fourth column shows that, on average, transient error accounts for 62% of observed faking effect size in personality scores. As a whole, these findings fully support Hypotheses 3 and 4.

Discussion

The main purpose of this study was to expand the literature on the effects of faking on personality measures by using an experimental design that permits us to control for the effects of transient error on the estimates of faking. As we previously pointed out, LSD is a type of experimental design that, due to its characteristics, allows us to control the effects of some sources of variability, such as transient measurement error, that other experimental designs (e.g., within-subject or between-subject designs) widely used in faking research cannot control. Because of this, LSDs are a more accurate way to know the consequences of faking because they reflect with more precision the true (real) effects of faking and the variance produced by other characteristics of the sample or the design.

Therefore, the current study has contributed to the study of faking and its effects in several ways. First, this study provides empirical evidence of the robustness of quasi-ipsative FC inventories resistance to scoring inflation in personality dimensions (i.e., the Big Five). In the current study this fact was shown by using a quasi-ipsative FC inventory that provides non-algebraically dependent scores.

Secondly, in accordance with the psychometric theory of faking effects (Salgado, 2016), the results showed that faking behavior increases the mean and decreases the standard deviation of personality scores which confirms the predictions of the theory.

The third contribution, and a unique one, has been to show that previous estimates of faking obtained with within-subject and between-subject experimental designs were affected by transient error to some extent. The transient error is a critical source of measurement error that can be substantial in some measures, e.g., faking (Becker, 2000; Schmidt et al., 2003; Vautier & Jmel, 2003). This study demonstrated that the transient error has a dramatic effect on faking estimates, as 62% of the faking effect size was due, on average, to transient errors. Consequently, it is of critical importance to take into account the potential effects of transient errors while keeping in mind the effect of transient error permits us to obtain two estimates of faking effect size, observed faking and true (real) faking. To the best of our knowledge, previous research has not distinguished between these two estimates of faking so far, and researchers have attributed the longitudinal variations in responses to personality measures due to random variation in respondents’ psychological states across time (i.e., transient error; Schmidt et al., 2003) to faking. Making this attribution, researchers implicitly assumed that the total amount of observed faking was true faking. Clearly this assumption was not supported in the current study.

From the methodological point of view, a third relevant contribution of the study has been to use an LSD to establish the real effects of faking. To the best of our knowledge, no previous research has used this design to examine faking effects. The LSD enabled us to estimate the amount of variability in honest and faking response conditions that it is misassigned to faking. The LSD showed that the experimental groups that responded both times under the same response instructions showed random variations that are not relevant to the construct under study, i.e., faking. In other words, the effect sizes were different from zero, contrary to the assumption of previous research.

The fourth contribution has been to show that, in comparison with SS personality inventories, quasi-ipsative FC inventories without algebraic dependence are a method capable of controlling the effects of faking on the scores. Globally, the d values provided by the current study are substantially smaller than those obtained for SS measures (e.g., Viswesvaran & Ones, 1999).

The fifth contribution has been to show that faking does not affect the Big Five personality factors equally in the personnel selection domain. Conscientiousness (d = 0.20) is the only personality dimension shown to be affected by faking but with no important practical consequences.

Implications for Research and Practice and Limitations of the Study

The findings reported in the current study have some implications for researchers and practitioners in applied personality assessment. From a research point of view, this is the first study that provides empirical evidence of the transient error effects of faking on personality measures. Therefore, empirical research should distinguish between observed faking and true faking when this construct is operationalized. The frequently used within-subject and between-subject designs do not permit us to distinguish between and to estimate the precise amount of these two estimates of faking, and this is critical as true faking is what it is truly relevant from an applied point of view.

From a practical perspective, the results supported the idea that quasi-ipsative FC personality inventories are robust instruments that control faking effects. Therefore, we suggest practitioners use quasi-ipsative FC personality inventories in applied settings (i.e., personnel selection) because, in addition to being relevant predictors of organizational outcomes (e.g., Martínez et al., 2021a; Salgado et al., 2015; Salgado & Táuriz, 2014), they are robust against faking.

This study, like any empirical study, has some limitations that should be considered in future research. First, this study used a single quasi-ipsative FC inventory, with its peculiarities (i.e., non-algebraic dependence). In this sense, future research should expand by using other FC formats (e.g., ipsative and normative FC inventories, and quasi-ipsative FC inventories with algebraic dependence). Second, although the findings of this study regarding transient error probably generalize to SS personality inventories, future studies should examine the extent to which transient error affects the faking estimates obtained for SS personality inventories. Hence, this study should be replicated with other types of personality inventories to confirm the generalization and extension of the findings.